基于信息熵的降雨信息区域化分析

张继国，吴 敏，谢 平，龚艳冰

(1.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072;2.河海大学水利信息统计与管理研究所，江苏 常州 213022)

降雨是水文模型的主要输入项，是影响流域水循环最活跃的因素，其时空分布不均匀性对流域产汇流的形成起着决定性的作用。越充分考虑降雨时空分布的不均匀性，水文过程模拟精度就越高［1-2］。对于大尺度流域而言，不同地区的降雨空间分布具有非常明显的不均匀性，所以，在研究大区域降雨量变化的同时，有必要研究该区域内不同地区的降雨量变化，这就使得降雨的分区尤为重要［3］。笔者［4］认为，在探讨降雨信息空间插值时，应首先将复杂的降雨测量站点系统划分成不同的子系统。近些年来，不少学者对我国不同区域的降雨进行了分区研究，取得了一定的研究成果［3，5-8］。

本文基于信息熵理论［9］和全信息原理［10］，就淮河流域蚌埠站以上99个雨量站进行划分，其目标是每个子区域的降雨信息具有最大的同质性，而不同子区域之间的降雨信息具有最大的异质性。本文的研究结论可为流域内站网优化布局、降雨不均匀性分析、降雨空间插值，以及建立分布式水文模型、极端洪旱灾害预报预警、水资源规划与利用、生态环境保护等研究提供科学依据。

1 基本知识与公式

设随机变量X具有n个可能状态，其概率分布为p=(p1，p2，…，pn)，则X的信息熵为

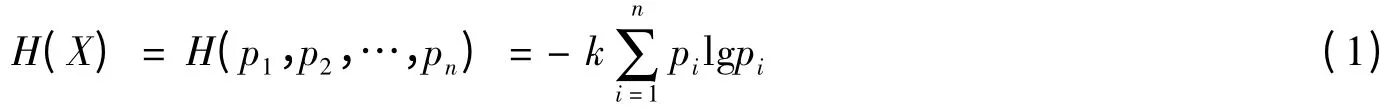
式中k≥0为常数。H有时被称为Shannon熵，它表示随机变量不确定性大小的度量。

设随机向量(X，Y)的联合概率分布为pij(i=1，2，…，n;j=1，2，…，m)，则(X，Y)的联合熵为

还可以相应地定义条件熵H(X/Y)和H(Y/X)。

互信息是两个变量相互包含信息量大小的指标，其定义为

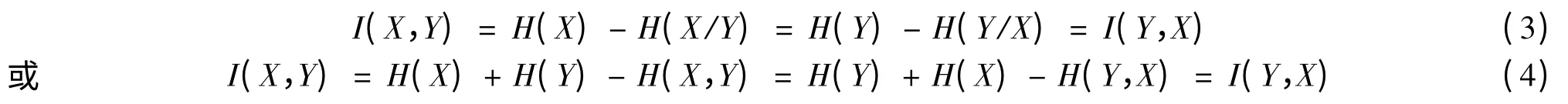
式(3)、式(4)表明X包含Y的信息等于Y包含X的信息。

信息的重要特征之一是具有传递性。X对Y的信息传递指数定义为

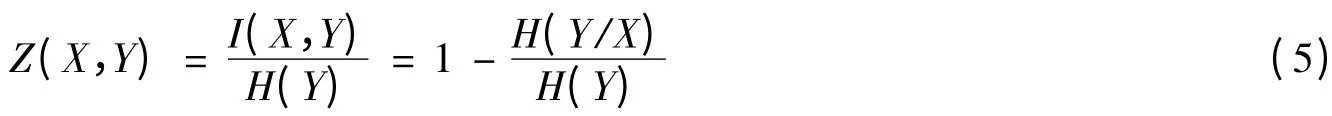
一般而言，信息传递指数Z不满足对称性。由于0≤H(Y/X)≤H(Y)，所以0≤Z≤1。当Z(X，Y)=0时，X对Y不存在任何信息传递;而当Z(X，Y)=1时，X包含了Y的全部信息。信息传递指数具有2个特征:(a)度量了信息点的信息传递能力，表示一个信息点对其周边的影响力;(b)描述了两信息点之间的相依程度，而这种相关往往是非线性的。

设S为包含了m个变量的集合，i∈S，称

为X在S中的综合信息传递指数［11］。根据这一指标，若某一站点在它所在的分区中ZS的值较高，则与同一区的其他站点相比应该被保留下来，而ZS值相对较低的点可以考虑被剔除。

ZS为绝对量。为了比较同一变量针对两个变量集合的相关程度，必须用到平均信息传递指数。设S包含m个变量，X∉S，则定义

为X对S的平均信息传递指数。

设S1和S2分别包含m1和m2个变量，X∉S1，X∉S2，根据式(7)以及信息传递的含义，若MS1(X)＞MS2(X)，则认为X可以归于S1。

众所周知，变量的信息熵只与其取值的统计特征有关，由此得到信息熵、互信息(包括信息传递指数)只是利用了变量的概率分布形式，或者说只是利用了变量的语法信息［10］。为了更全面地研究变量间的差异性，本文同时考虑变量的语义信息，即考虑变量的取值。为此，给出两个随机变量的贴近度指标。

设有随机变量X={x1，x2，…，xn}和Y={y1，y2，…，yn}，它们之间的贴近度定义为

由式(8)可见，T(X，Y)越小，则X，Y之间的差异越小，贴近度越高。

本文采用等间距法［12］求取随机变量的信息熵或联合熵。确定分组数时可采用经验公式［13］:

式中n为样本容量。

2 研究思路与数据处理

2.1 数据来源

淮河流域介于长江和黄河两大流域之间，气候上处于南北气候过渡带，降雨时空分布严重不均。本文研究的99个雨量站［14］位于淮河流域蚌埠站以上区域，东经112°～118°、北纬31°～35°之间。

降雨资料取自各雨量站1953—2010年共58 a的月平均降雨序列，该序列构成为降雨随机变量，则降雨随机变量共有696个月降雨数据。

2.2 研究思路

该研究区域内的降雨信息区域化过程分为3个步骤。

a.根据信息熵的等距离法，首先将每个站的降雨序列样本划分为若干个小区间，计算每个站的信息熵和联合熵，在此基础上构建99个站的信息传递指数矩阵。以该矩阵作为模糊关系矩阵，根据模糊聚类法将99个站划分成不同的分类(子区域)。

b.最佳分类标准就是类与类之间存在较大的差异，而每一类内部的差异性则较小。因为Z刻画的仅是两个变量间在概率分布形式上的差异性，而没有反映变量间取值的差异性问题。以全信息理论的观点来看，Z或者H是语法信息的表现，而变量的取值则属于语义信息。所以，本文考虑的这种差异性大小即是以站点之间降雨量的贴近度来度量的，同一时刻的降雨量越接近，则认为差异性越小。依照降雨量贴近度指标，对各种分类进行显著性检验，在不同的分类中初选出若干个最能符合标准的分类。

c.以平均信息传递指数作为判别标准对其初始分类予以进一步调整，最终确立最佳分类。

2.3 数据处理

将每个站点的696个降雨数据从小到大排序，按式(9)将其取值区间等距离划分成26个子区间，记每个小区间δi(i=1，2，…，26)，记落在小区间δi的降雨数据数为ni，所以，降雨数据X落在δi内的概率pi近似等于其频率ni/696。同理，将2个站点X，Y的降雨数据构成的区域划分成面积相等的262个子区域Δij(i=1，2，…，26;j=1，2，…，26)。假设落在某个子区域Δij的点对数(频数)为nij，而总的点对数为696×696，则降雨数据落在该子区域的概率pij近似等于频率nij/6962。然后，利用式(1)和式(2)分别计算99个站点降雨量的信息熵以及两两间的联合熵。

利用式(4)计算互信息，根据式(5)可得到信息传递指数矩阵D=(dij)99×99，其中dij为第i号站对第j号站的信息传递指数。利用式(8)计算99个站点的降雨量贴近度矩阵N(tij)99×99，其中tij表示为第i号站与第j号站的贴近度。利用软件Matlab R2011a完成全部计算过程。

3 区域划分与调整

3.1 初始分类

将D作为模糊关系矩阵，利用模糊聚类方法［15］对99个站点予以分类。首先将其分别分成3，6，7，8，10，11，12，14，15，18，20，22，24和28类。每类所包括的站点见图1，其中，第1区包含62个站，第2～6区分别含有10，19，1，4，3个站。

为确定最优分类，利用N(tij)99×99对以上划分进行显著性检验(取显著性水平α为0.05)。先假设99个站点被分成了r类，每类所含站点数为ni。根据数理统计理论，统计量F服从F分布。

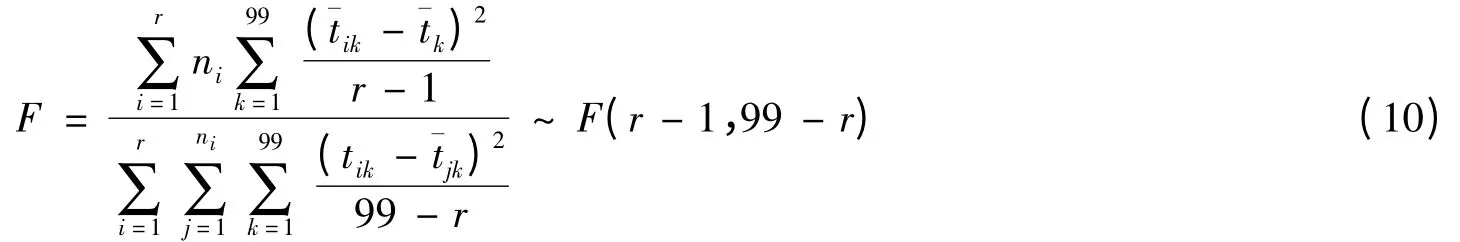
F值越大，或(F-Fα)越大，则类与类之间的距离越大，相应的分类就越优。具体检验结果见表1。

从表1可见，将区域分成3类或6类比较合适。先以分成6类的情况作为调整基准。

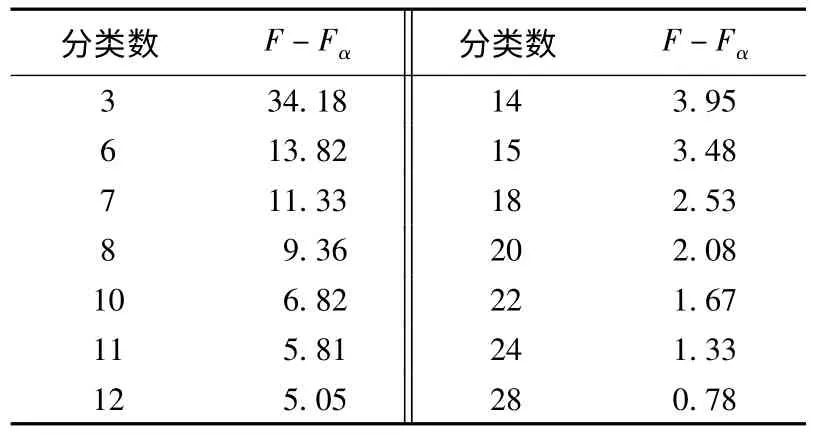
表1 F检验结果Table 1 F-test results

3.2 调整过程

仔细分析图1可见，除了第4区仅一个站点外，其余各类所包含站点大多在地理位置上较为接近，但也有部分相互交叉，使得区域边界不够清晰。由于前3类包含站点较多，为此以这3类为主体对相关站点予以调整(被调整站点编号见表2)，调整标准为待调整站点对于各区的平均信息传递指数。根据平均信息传递指数值的大小(表2)，决定待调整站点被调整进哪个区。如，47号站点初始划分时处于第2区，但因为对第1区、第2区、第3区的平均信息传递指数分别为0.1657，0.1864，0.221 8，根据本文的分析，它应该被调整到第3区。

经过以上调整后子区域的状况是，第1区包括53个站点，第2区包括19个站点，第3区包括20个站点，第4区包括4个站点，第5区包括3个站点。

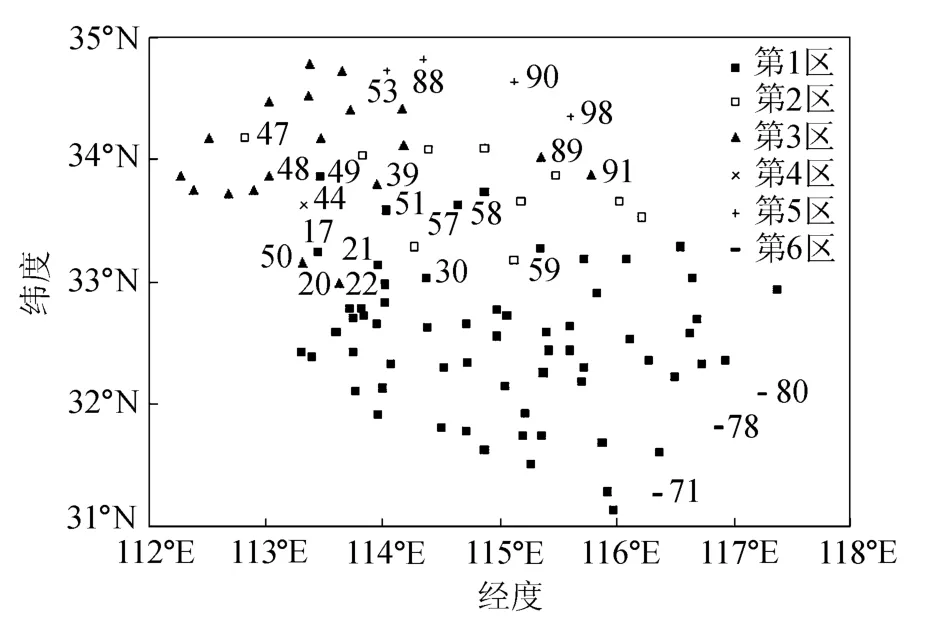
图1 淮河流域蚌埠站以上99个站划分成6类站点分布Fig.1 99 stations upstream of Bengbu Station in Huaihe River Basin divided into six categories

最后将第4区、第5区的站点进行调整(见表2)，这样全部99个站被划分为3个区域，其中A区包括56个站点，B区21个，C区22个(见图2)。

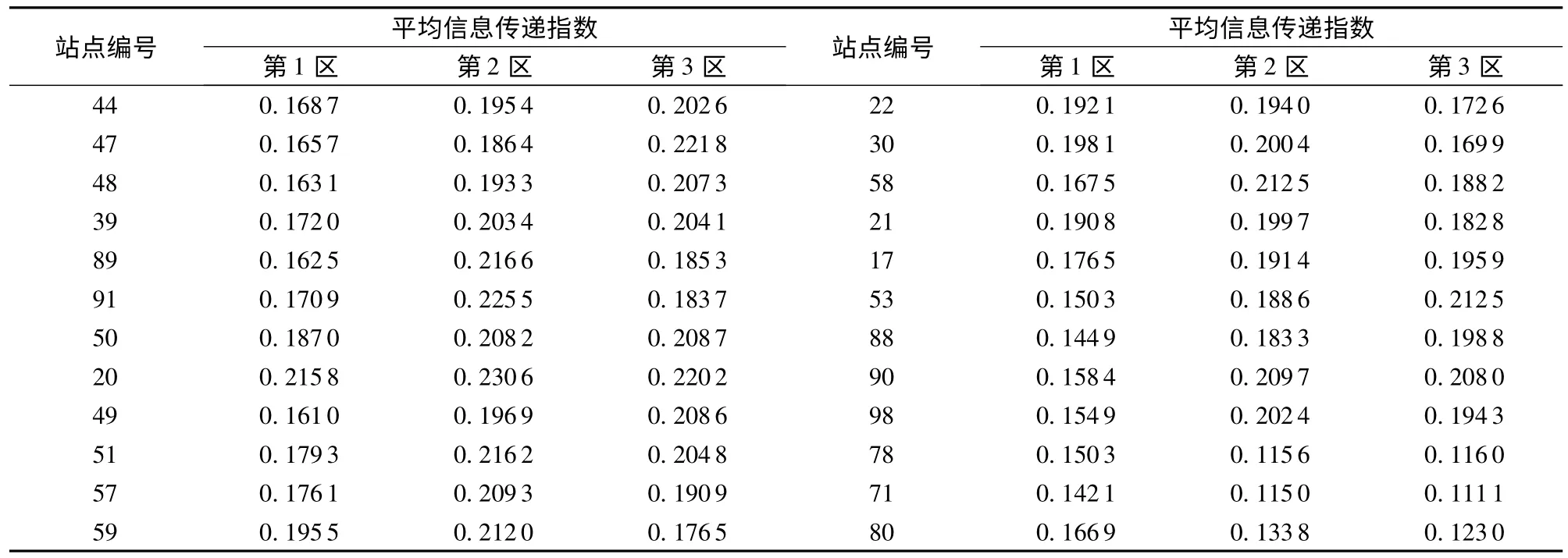
表2 待调整站点对各区平均信息传递指数Table 2 Average information transmission values of Stations to be adjusted in each district

对最终分成3个子区域的情况予以F检验，得F-Fα=39.16，可见各子区域内降雨信息的同质性和子区域间的异质性是显著性的。

3.3 讨论

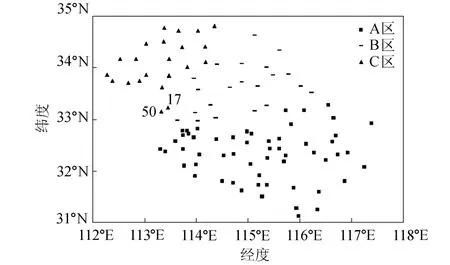
图2 淮河流域蚌埠站以上99个站划分成3类站点分布Fig.2 99 stations upstream of Bengbu Station in Huaihe River Basin divided into three categories

需要说明的是，站点50号和17号虽然归类于C区(见图2)，但它们对B区、C区的平均信息传递指数较为接近，所以为了各子区域在地理位置上更为完整，可考虑将这2个站点划分到B区。

尽管最终将所研究区域划分成3个子区域，从划分的情况来看，各子区域所含的站点有些偏多，尤其是A区包含56个站。如果具体研究所需，可以将每一个子区域作为单独的研究对象，利用本文的方法予以再行划分。例如，将A区再划分成2类、3类不等。

4 结 语

将复杂性大系统根据一定的原则划分成若干子系统，使各子系统内具有较大的相似性，而子系统之间具有较大的相异性，符合系统论的观点，而且便于研究复杂性的数据系统，有利于探寻大系统内的不确定性规律，如降雨的不均匀性研究。本文以信息熵作为研究手段，结合信息的语法形式和语义形式，对淮河流域蚌埠站以上区域进行了区域划分，因而这种划分的方法符合信息科学原理，即具有更高的可靠性。从分类的情况观察，各类区域内的站点在地理位置上相当接近，虽然从初步的划分中区域间有所交叉，但是经过调整后，区域间的边界变得较为清晰。

［1］梁忠民，李彬权，余钟波.考虑空间变异性的统计产流模型研究［J］.南京大学学报:自然科学版，2009 45(3):403-408.(LIANG Zhongmin，LI Binquan，YU Zhongbo.A statistically-based runoff-yield model considering spatial variation［J］.Journal of Nanjing University:Natural Sciences，2009，45(3):403-408.(in Chinese))

［2］姜红梅，任立良，袁飞.降水空间不均匀性对径流过程模拟的影响［J］.水文，2004，24(2):1-6.(JIANG Hongmei，REN Liliang，YUAN Fei.Effect of spatial precipitation heterogeneity on runoff process［J］.Journal of China Hydrology，2004，24(2):1-6.(in Chinese))

［3］郑永宏，林爱文，代侦勇.湖北省降水分区研究［J］.长江流域资源与环境，2012，21(7):859-863.(ZHENGYonghong，LIN Aiwen，DAI Zhenyong.Research on precipitation regionalization in Hubei Provence［J］.Resources and Environment in the Yangtze Basin，2012，21(7):859-863.(in Chinese))

［4］张继国，谢平，龚艳冰，等.降雨信息空间插值研究评述与展望［J］.水资源与水工程学报，2012，23(1):6-9.(ZHANG Jiguo，XIE Ping，GONG Yanbing，et al.Review and perspectives of the research on spatial interpolation of rainfall data［J］.Journal of Water Resources＆Water Engineering，2012，23(1):6-9.(in Chinese))

［5］秦爱民，钱维宏.近41年中国不同季节降水气候分区及趋势［J］.高原气象，2006，25(3):495-502.(QIN Aimin，QIAN Weihong.The seasonal climate division and precipitation trends of China in recent 41 years［J］.Plateau Meteorology，2006，25(3):495-502.(in Chinese))

［6］杨绚，李栋梁.中国干旱气候分区及其降水量变化特征［J］.干旱气象，2008，26(2):17-24.(YANG Xuan，LI Dongliang.Precipitation variation characteristics and arid climate division in China［J］.Arid Meteorology，2008，26(2):17-24.(in Chinese))

［7］李生辰，徐亮，郭英香，等.近34 a青藏高原年降水变化及其分区［J］.中国沙漠，2007，27(2):307-314.(LI Shengchen，XU Liang，GUO Yingxiang，et al.Change of annual precipitation over Qinghai-Xizang Plateau and sub-regions in recent 34 years［J］.Journal of Desert Research，2007，27(2):307-314.(in Chinese))

［8］孙莹，万丽岩，江静.辽宁降水分区变化特征及夏季降水影响因子分析［J］.气象与环境学报，2008，24(3):18-23.(SUN Ying，WAN Liyan，JIANG Jing.Characteristics of precipitation division and controlling factors of summer precipitation in Liaoning Province［J］.Journal of Meteorology and Environment，2008，24(3):18-23.(in Chinese))

［9］张继国，刘新仁.水文水资源中不确定性的信息熵分析方法综述［J］.河海大学学报:自然科学版，2000，28(6):32-37.(ZHANG Jiguo，LIU Xinren.Summary on the information entropy analysis methods of uncertainty in hydrology and water resources［J］.Journal of Hohai University:Natural Sciences，2000，28(6):32-37.(in Chinese))

［10］钟义信.信息科学原理［M］.3版.北京:北京邮电大学出版社，2002.

［11］YANG Y，BURN D H.An entropy approach to data collection network design［J］.Journal of Hydrology，1994，157:307-324.

［12］丁晶，王文圣，赵永龙.以互信息为基础的广义相关系数［J］.四川大学学报:工程科学版，2002，34(3):1-5.(DINGJing，WANG Wensheng，ZHAO Yonglong.General correlation coefficient between variables based on mutual information［J］.Journal of Sichuan University:Engineering Science Edition，2002，34(3):1-5.(in Chinese))

［13］庄楚强，吴亚森.应用数理统计基础［M］.广州:华南理工大学出版社，1992.

［14］张继国.降雨时空分布不均匀性信息熵研究［D］.南京:河海大学，2004.

［15］王忠玉，吴柏林.模糊数据统计学［M］.哈尔滨:哈尔滨工业大学出版社，2008.