液位标准装置的不确定度分析

刘 硕，穆 克，佟仕忠，付贵增

（辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001）

液位仪表常用于过程控制中的液位监测。近年来，石油工业对油罐液位计量的自动化要求不断提高，使得液位仪表在油罐计量领域崭露头角。由于进行贸易交接的立式金属罐容量较大，十分微小的测量误差都会造成很大的绝对误差[1-2]。

2008年国际计量组织（OIML）发布了 R85（用于测量储油罐的液位仪表）[3]。这标志着液位仪表应用于油罐计量领域被国际计量组织认可，可作为计量器具用于商业交接中。在国家授权下现已建立起液位标准装置，用于检定和标定各类液位计计量仪表，按照国家标准完成一个认证任务。由于该装置要求有极高的精度（±100 μm），所以需要考虑各方面因素对其最终测量精度的影响，并得出最终的不确定度评定[4]。

1 液位标准装置的测量原理

如图1所示，液位标准装置是由双频激光干涉仪、浮子和25 m高立式储罐构成。双频激光干涉仪竖直的置于标准罐顶部，激光透过标准罐顶部的玻璃照射到浮子上的全反射棱镜（锥体棱镜），全反射棱镜将照射来的激光按原光路反射回双频激光发射器内的接收装置。当液位变化时，浮子的位置随之变化，双频激光发射器到浮子的距离也就跟随着浮子的高低发生了变化。由此，利用双频激光干涉仪的测量原理测量液位。

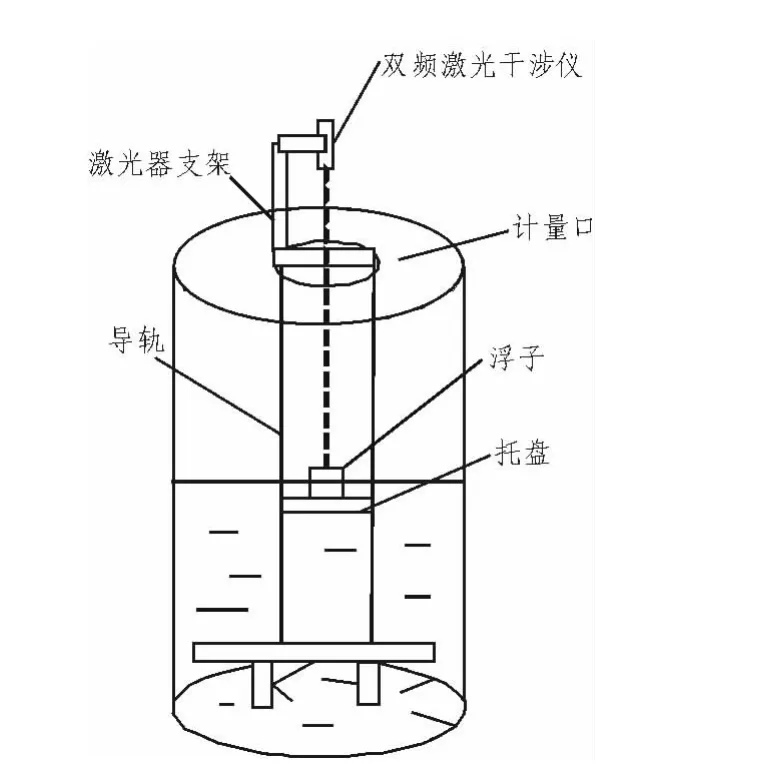
图1 液位标准装置原理结构图Fig.1 Structure diagram of liquid level standard device

2 不确定度评定

分析装置结构和测量方法可知，液位标准装置测量的主要不确定度有：浮子浸没深度不确定度；光路对测量精度影响引起的不确定度；双频激光干涉仪本体的影响等。下面对各主要因素引起的不确定度分量进行分析与计算。

2.1 浮子浸没深度影响引起的不确定度分量

原理

如图2所示，内浮子上半部分为圆柱，底部为圆台，浮子受到自身重力和浮力，所以根据阿基米德原理及圆台、圆柱的体积计算公式可计算出浮子浸没深度

图2 内浮子结构图Fig.2 Structure diagram of inside float

其中：h为浮子浸没深度，h圆台为浮子圆柱部分浸入液体的高度；ρ水为水的密度；m为浮子质量；h圆台为圆台高度；R为圆台大圆半径；r为圆台小圆半径。分析其特点可知，此不确定度采用B类判定方法。

又 R=4.597 25×10-2m，u（R）=3×10-6m；r=1.502 4×10-2m，u（r）=3×10-6m；m=0.403 893 kg，u（m）=2×10-6kg；

浮子整体高度：h=0.120 005 m，浮子圆柱部分高度：h′=0.110 053 m，且 u（h）=3×10-6m，u（h′）=3×10-6m；

注：在此已考虑温度对水的密度的影响。经过计算得知，在15~25℃范围内，水在15℃时的不确定度最大。

密度计最大允许误差为0.1 kg/m3，服从均匀分布[5]：

根据不确定度计算公式可得

2.2 光路对测量精度影响引起的不确定度

Edlen公式及其修正公式，是以温度、压强、水蒸气压力为参数的公式。一般由湿度计测量出的是相对湿度值，而不是蒸汽压力值。因此，Edlen公式及其修正公式在应用中受到了限制，需转换为以相对湿度为参量的大气折射率的计算公式[6]

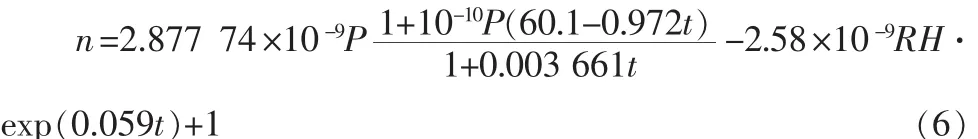
式中，P为气体压强；t为气体温度；RH为相对湿度；分析其特点，该不确定度采用B类判定方法[5]。

2.2.1 压强测量引起的不确定度

压强的测量采用的是压力变送器，量程为70～120 kPa，准确度为0.5%FS，所以全量程的标准不确定度为：

又在压强为101.325 kPa、温度为20℃、湿度为 60%条件下：

所以由压强测量引起的不确定度分量

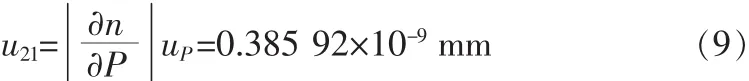
2.2.2 温度测量引起的不确定度

所以由温度引起的不确定度分量为：

2.2.3 相对湿度测量引起的不确定度

相对湿度的测量采用的是温湿一体变送器，湿度量程为（0～100）%RH，准确度为±1%rh，所以由相对湿度引起的标准不确定度

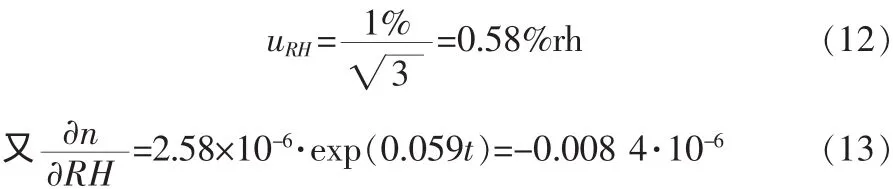
所以由相对湿度引起的不确定度分量

2.2.4 以相对湿度为参量的大气折射率公式引起的不确定度

通过计算可知，该公式引起的不确定度为5×10-8。公式的精度包括以下3项：改进Ellen公式的不确定度3×10-8；简化误差约±100 Pa，对大气折射率计算值的影响±3.6×10-8；假定 CO2含量偏离100 ppm，对大气折射率计算值的影响±1.5×10-8。

2.2.5 光路对测量精度影响引起的不确定度合成

因为 P、t、RH 相互独立，所以

2.3 重复性试验带来的不确定度

表1为同一液位下短时间内10次测量结果。

该不确定度采用A类判定方法，得出

表1 重复试验测量值Tab.1 Repeat measurements value

2.4 双频激光干涉仪本体的影响

根据产品说明书可知，干涉仪的误差为1 ppm，也就是±1×10-7mm，该不确定度采用B类判定方法，所以

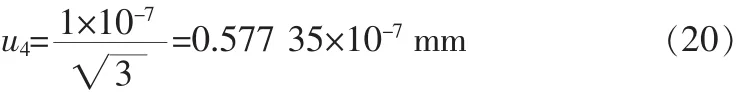
3 不确定度合成

各不确定度分量相互独立，所以

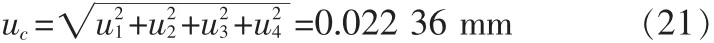
4 展伸不确定度

取包含因子k=3，则展伸不确定度

5 结 论

通过对液位标准装置的结构及测量原理[7]的分析，罗列出了各影响因素的不确定度分析，并进行不确定度的合成，最终得出液位标准装置测量标准不确定度uc为0.022 36 mm，展伸不确定度U为0.067 08 mm。

[1]罗志勇，刘子勇.液位计标准检测系统设计[J].现代计量测试，1998（6）：27-29.

LUO Zhi-yong，LIU Zi-yong.Design of level gauge test system[J].Modern Measuring and Testing，1998（6）：27-29.

[2]李冬梅.国内外液位计量仪表技术发展动向[J].仪器仪表用户，2002（3）：5-7.

LI Dong-mei.Domestic and overseas development trend of level measurement instrument technology[J].Instrument User，2002（3）：5-7.

[3]International organization of legal metrology.R85.Automatic level gauges for measuring the level of liquid in stationary tank[S].International organization of legal metrology:Paris.2008.

[4]国家质量监督检疫检验总局JJG971-2002液位计检定规程[S].上海：上海市计量测试技术研究院，2002.

[5]费业泰.误差理论与数据处理[M].北京：机械工业出版社，2000.

[6]Edlen B.The refractive index of air[J].Metrologia，1996（2）：71-80.

[7]马伟.超声波液位计的误差分析与校正[J].电子科技，2011（4）:107-109.

MA Wei.Error analysis and correction of Ultrasonic level meter[J].Electronic Science and Technology， 2011（4）:107-109.