均匀圆阵部分阵元失效情况下的DOA估计方法

张宏谋，闫剑虹，施锦文

（中国空间技术研究院西安分院 陕西 西安 710100）

在实际的DOA估计中，由于均匀圆阵（Uniform Circular Array，简称 UCA）具有诸多优点，比如：可对俯仰角和方位角同时进行估计，且可覆盖较宽的频带，具有 360°的方位角观察范围；当所取的阵元数是大于5的奇数或是大于 8的偶数时，不存在取向模糊；并且，由于均匀圆阵具有对称性，因而在各方位角上有着一样的方向特性[1]。针对相干信号，均匀圆阵可以采用模式空间变换法[2-4]和平滑技术[5-7]来实现解相干。文献[8]将圆阵划分为子阵，并对其进行加权，然后进行超分辨估计。因此，它是在实际当中经常采用的一种阵列结构。但是，一旦均匀圆阵某一个或几个通道出现故障，通道的数据变成无效数据，对于超分辨算法如MUSIC算法[9]，则会导致测向性能的严重恶化，甚至测向失效。

针对此问题，文中提出在均匀圆阵部分通道失效的情况下，利用均匀圆阵有效阵元数据实现对信号来波方向进行估计的方法。该方法能在部分阵元数据失效的情况下，仍然取得良好的估计性能。

1 均匀圆阵模型

设在平面内半径为r的圆周上均匀分布着 M个相同的全向天线，参考点为阵列圆心。俯仰角φ是入射信号与z轴之间的夹角，方位角θ是入射信号沿逆时针方向与x轴的夹角。均匀圆阵的阵列模型如图1所示。

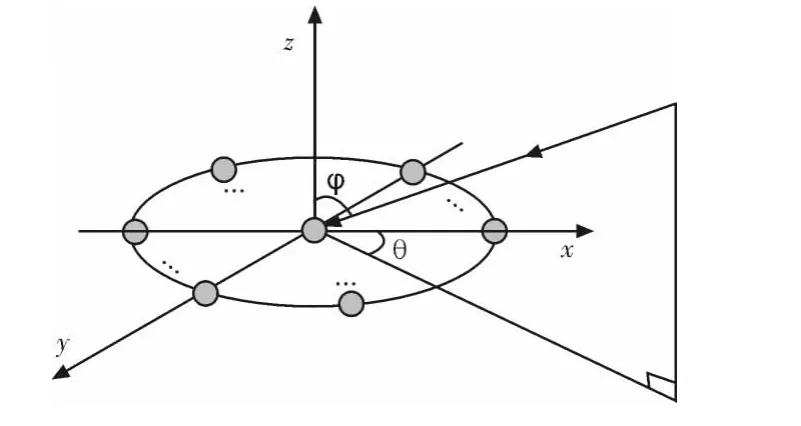
图1 均匀圆阵模型Fig.1 Model of the UCA

均匀圆阵共有 M个阵元，共有 N个信号 si（t），i=1~N，第i个信号入射方向（θi，φi），则第 k 个阵元接收的数据为：

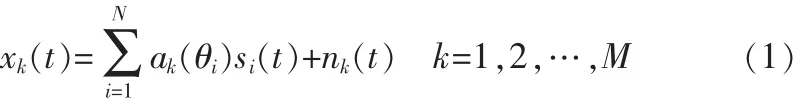
写成矢量形式如下：

X（t）为 M×1 维快拍数据矢量，S（t）为 N×1 维信号数据矢量N（t）为M×1维噪声数据矢量，A为空间阵列的M×N维导向矢量矩阵。其中

2 部分阵元失效情况下的均匀圆阵测向

2.1 均匀圆阵的MUSIC算法

MUSIC算法[10]是经典的超分辨算法，其对阵列接收数据的协方差矩阵进行特征分解，得到噪声子空间和信号子空间，利用噪声子空间进行谱峰搜索，进行波达方向估计。

阵列接收数据的协方差矩阵为：

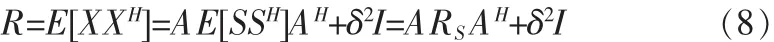
进行特征分解有:

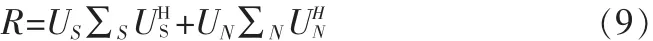
式（9）中，US是由大特征值对应的特征矢量张成的信号子空间，UN为由小特征值对应的特征矢量张成的噪声子空间。对实际数据矩阵，数据协方差矩阵的最大似然估计为：

对Rˆ进行特征分解，可以得到噪声子空间特征矢量矩阵UˆN。 由于噪声的存在 a（θ）与UˆN并不能完全正交，实际上是以进行方位角优化搜索实现DOA估计的。当进行一维DOA估计时，即是求 aH（θ）UˆNUˆHNa（θ）的最小值。 因此，MUSIC 算法的谱估计公式为：

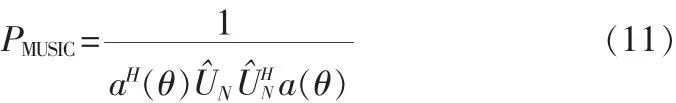
2.2 均匀圆阵隔离故障阵元测向原理

均匀圆阵用MUSIC算法测向时，一旦阵元通道出现故障，则阵元的数据变成无效数据，会导致测向性能的严重恶化。这是由于，对于故障阵元而言，其数据特性可能已经和正常数据的特性完全不一致，其数据的振幅，相位等有可能呈现出随机数值的特点，尤其是相位的错乱，是影响MUSIC算法的关键因素。所以，一个或几个阵元振幅，相位的错乱，会导致整个阵列测向性能的严重下降，甚至完全失效。

1）均匀圆阵隔离故障阵元分析

对于MUSIC算法而言，对于阵列的结构是没有特殊要求的，它并不像ESPRIT算法那样需要阵列具有旋转不变性。也就是说，对于任意结构的天线阵列，我们都能够用MUSIC算法进行测向，这也就是本文提出隔离故障阵元的原理所在。下面我们举例说明。

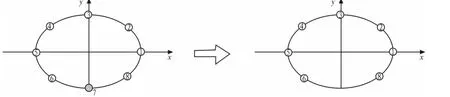
图2 均匀圆阵故障阵元隔离原理Fig.2 Principle of isolating the failed sensor

图2为8阵元均匀圆阵隔离故障阵列的原理示意图。对于8阵元均匀圆阵，假定阵元7出现故障，此时，我们将其隔离后的阵列结构相当于一个7阵元面阵，此时其阵元数为7，但是已经不是均匀圆阵。由于此时阵元数目下降了1，故其可测向的信号数目最多将变为6。这也意味着阵列孔径的损失。同理，每当故障阵元增加一个，阵列可测向的信号数目将减少一个。我们可以得到阵元故障时，阵列可测向信号的数目为：

上式中，NS为阵列可测向信号的最大数目，M为整个阵列的阵元数目，NF为故障阵元的数目。

2）构造非均匀圆阵阵列数据

由上节可知，直接将故障阵元隔离掉，可以利用部分有效阵元形成的非均匀圆阵进行测向。下面说明利用剩余的有效阵元构造接收数据的方法。我们仍然以8阵元为例进行说明。设阵列为8元均匀圆阵，故障阵元为7号阵元，则利用其余有效阵元构成的阵列数据如下：

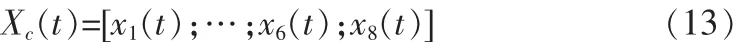
其中，Xc（t）为重构的数据矩阵，Xi（t）为第 i个阵元的接收数据。此时，由于阵元数目少一个，数据的结构在阵元的维数上较之原阵列要少一维，所以整个阵列的数据矩阵行的维数较原阵列要少一维。

3）利用构建的7元面阵测向

假定只进行方位角测向，即认为俯仰角为90°，得到MUSIC测向算法如下：

其中：a（θ）=[exp（-jω0τ1）]exp（-jω0τ2）… exp（-jω0τ6）exp[（-jω0τ8）]T，τi为第 i个阵元相对于参考阵元的时延。 因此，我们构造的7阵元面阵和原8阵元相比较，其阵列结构发生变化，在进行谱峰搜索的过程中，其导向矢量也应该相应的做出调整，不能以原导向矢量进行测向。

3 性能仿真

为简化分析，我们以一维方位角测向进行仿真实验。不失一般性，阵列采用8元均匀圆阵，阵元间距采用最高频率的半波长，即 d=λ/2，快拍数为 500。

仿真实验1：8阵元中3阵元故障对测向的影响

1）3 阵元故障性能。阵元 2，5，7 故障，信号数目为 3，来波方向为[50，120，245]°。 噪声为加性高斯白噪声，信噪比 10 dB，取50次独立试验的均值。仿真中故障阵元数据采用随机数据，其方差等于信号功率。其仿真结果如图3（a）所示，当阵元2，5，7故障时，空间谱估计完全失效；而没有故障时，阵列的测向性能优良。

2）隔离3故障阵元时的测向性能。从图3（b）中可以看出，隔离故障阵元后的阵列测向性能良好，能够精确的测出所有3个信号的方位。

仿真实验2：8元均匀圆阵与重构阵列测向精度的比较

设有一感兴趣信号，波达方位角为45°，现考虑在不同信噪比条件下，真实阵列无故障时和阵元2，5，7故障时本文重构阵列的测向精度。仿真进行50次独立试验，50次仿真的误差均值结果如图4（a）所示。可以看到，故障阵列按照本文方法重构后的测向性能在信噪比较低时略差于阵列无故障时测向性能。而在信噪比较高时，二者测向性能一致。

图4（b）为两种算法在不同信噪比下的均方根误差。与误差性能相似，在较低信噪比条件下，本文算法的均方根误差略大于原阵列，当信噪比较高时，二者测向性能一致。因此，本文算法具有较好的估计精度及鲁棒性，其在低信噪比条件下仍然能够实现优良的估计性能。

4 结 论

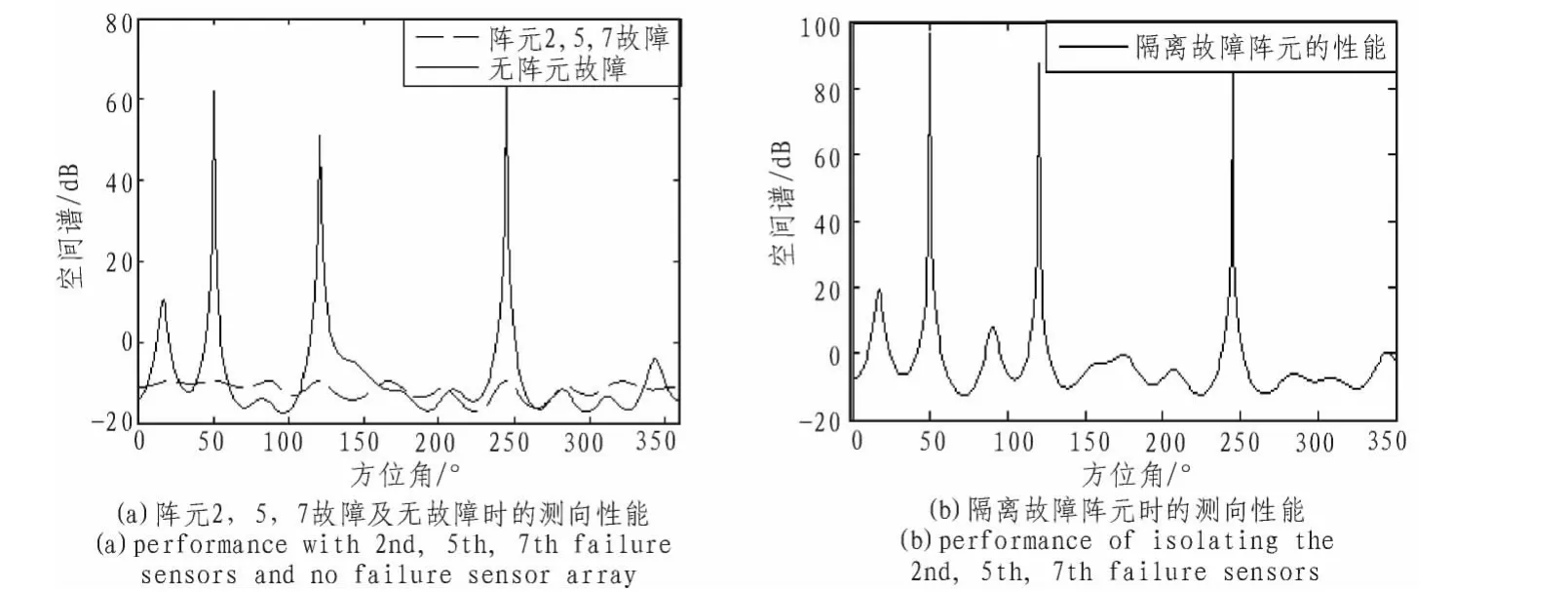
图3 阵元故障时对阵列测向的影响Fig.3 Influence of failed sensor to the performance of array

图4 重构阵列和原阵列精度比较Fig.4 Accuracy difference between the reconstructed array and the original array

文中对在均匀圆阵部分通道失效的情况下，利用均匀圆阵[11]有效阵元数据实现对信号来波方向进行有效估计的方法进行了理论上的分析和仿真实验的验证。其通过对实际阵列的故障阵元进行隔离，利用剩余阵元的数据，进行高分辨的MUSIC算法测向。该方法能在较高信噪比条件下实现和原阵列几乎相同的估计精度，在较低信噪比、信号数较小的条件下，也能取得良好的估计性能，大大增强了整个阵列谱估计的稳健性和鲁棒性，计算机仿真对该方法的有效性进行了验证。

[1]刘艳.基于均匀圆阵的波达方向估计算法的性能研究[D].重庆:重庆大学，2011.

[2]Wax M，Sheinvald J.Direction finding of coherent signals via spatial smoothing for uniform circular arrays[J].IEEE Trans on Antenna and Propagation，1994，42（5）:613-619.

[3]韩晓东，刁鸣.冲击噪声背景下均匀圆阵相干信源的DOA估计[J].应用科技.2012.39（1）:35~38

HAN Xiao-dong，DIAO Ming.DOA estimation of uniform circular array and coherent sources in an impulsive noise environment[J].Applied Science and Technology，2012，39（1）:35-38.

[4]杨海洋，王东进，陈卫东.一种模式空间中的快速DOA估计算法[J].中国科学技术大学学报，2010，40（8）：771-775.

YANG Hai-yang，WANG Dong-jin，CHEN Wei-dong.A fast approach to DOA estimation within mode space[J].Journal of University of Science and Technology of China，2010，40（8）：771-775.

[5]Shan T J，Wax M，Kailath T.Adaptive beamforming for coherent signals and interference[J].IEEE Trans.on ASSP，1985，33（3）:527-536.

[6]Williams R T，Prasad S，Mahalanbis S K，et al.An improved spatial smoothing technique for bearing estimation in a multipath environment[J].IEEE Trans.on ASSP，1988，36（4）:425-432.

[7]董玫，张守红，吴向东，等.一种改进的空间平滑算法[J].电子与信息报，2008，30（4）:859-862.

DONG Mei，ZHANG Shou-hong，WU Xiang-dong，et al.An improved spatial smoothing technique[J].Journal of Electronics&Information Technology，2008.30（4）:859-862.

[8]苏成晓，罗景青.一种均匀圆阵子阵干扰抑制DOA估计算法[J].信号处理，2010，26（9）:1355-1360.

SU Cheng-xiao，LUO Jing-qing.A novel DOA estimation algorithm via subarray jamming suppression based on uniform circular array[J].Signal Processing，2010，26 （9）:1355-1360.

[9]Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Trans.on AP，1986，34（3）:276-280.

[10]王永良，陈辉，等.空间谱估计理论与算法[M].北京：清华大学出版社，2004.

[11]黄珂.均匀圆阵列参数分析[J].电子科技，2012(5):8-9,13.

HUANG Ke.Analysis of uniform circular array parameter[J].Electronic Science and Technology，2012（5）:8-9,13.