基于主元熵的发动机能量数据聚类与故障识别*

李怀俊 谢小鹏 黄恒

(华南理工大学 汽车摩擦学与故障诊断研究所，广东 广州 510640)

发动机状态监测与故障模式识别是借助一定的有效方式及发动机各种状态信息，结合先验知识进行信息的综合处理，进而得到关于系统运行状况和故障状况的综合评价的过程.现有的发动机故障识别方法可分为基于动态数学模型的方法、基于信号处理的方法和基于知识的智能识别方法［1-2］.通常做法是采取小波变换、经验模态分解等方法处理振动等非线性信号，提取典型故障特征，进而运用神经网络、支持向量机、粗糙集等基于知识的智能识别方法进行故障判别［3-4］.在此过程中，由于故障原因与征兆的映射关系呈现不确定性及闭环非线性，基于模糊聚类方法的故障模式识别成为智能识别方法中的研究热点与难点，且被证明是一类有效的振动故障识别方法［5-8］.文献［7］在对故障样本特征加权的基础上，用混沌优化方法求解聚类目标，在振动故障诊断中取得了不错效果.文献［8］将局部均值分解和模糊k 均值(FKM)聚类算法相结合对故障进行识别分类，对小样本振动数据特征提取效果明显.同时此类方法中普遍存在以下问题:①为提高识别效果可能选取的单个故障的特征参数过多，直接送往识别模块进行训练会因数据维数过高或带有强噪声干扰而严重恶化识别器的聚类效率和故障判别能力，需采取有效方法进行特征降维.②常用的FKM等算法存在缺陷:对初始值敏感聚类的类数不能自动确定［9］，使用时必须确定聚类的有效性准则;类中心的位置和特性不一定事先知道，必须随人为设定的初始隶属度随机产生;收敛速度慢，容易陷入局部极值点而得不到最优分类.因此需寻找有效方法解决初始值敏感及分类数无法自动确定等关键问题.

基于此，文中提出了主元信息熵的概念，以及将其和FKM 算法相结合形成的故障模式模糊识别方法.同时提出了面向发动机能量数据(而非常用的振动信号)进行分析的策略，针对喷油脉宽等能量数据进行处理，寻求不同故障模式下数据降维后的聚类中心和识别特征，实验结果验证了方法的高效性.

1 发动机系统能量分析

发动机系统属于典型闭环控制系统，多个检测传感器输出大量强耦合性数据，数据流能够动态反映发动机的实际工作状态.若系统工况不变，则能量耗损在正常的范围内，其工作状态是稳定的;若能量耗损发生明显变化，则运动副的磨损或者振动加剧，数据流发生异常［10］.发动机系统的输入输出能量耗损关系如下:

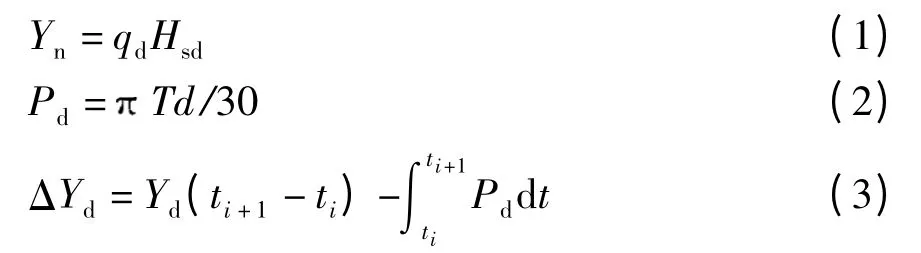
式中:Yd为燃油能量;qd为燃油流量;Hsd为单位标准燃油体积的高位发热量;Pd为发动机输出功率;T 为输出扭矩;d 为转速;ΔYd为发动机系统的能量耗损，其中包括摩擦发热、振动噪声和尾气排放等能耗;ti为第i 次检测的起始时间.

从能量转移的角度看，故障数据流中燃油压力、喷油脉宽、燃油修正值、氧传感器电压、节气门开度等5 个参数与燃油和空气有关，属于较典型的能量数据，其在故障状态下的变化量将影响式(1)、(2)中的参数，可以较全面地反映系统的能量耗损情况.因此运用这些能量特征数据进行发动机故障识别具有重要的研究意义.

2 主元能量特征提取

主元特征提取基于主元分析法［11］，可对原始数据降维分析、约简，有效找出故障数据中最“主要”的数据和结构，去除冗余和噪音，且无参数限制.

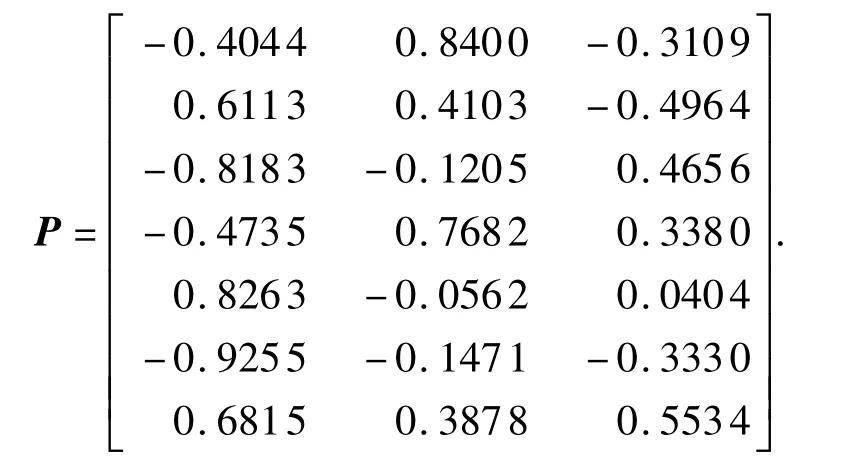
设X=(x1，x2，…，xn)T，为一n 维随机向量，其分量均值为零，即E(xi)=0(i=1，2，…，n).考虑协方差矩阵A=E［XXT］，设1≥2…≥n≥0 为A 的n 个特征值，则存在正交矩阵P 使得PTAP =Λ，其中Λ =diag(1，2，…，n)，为对角阵.令Y =PTX，因Yi均值为零，i即为其方差，有为A 的对角元素为X 的平均能量.设α 界于0～1，若(Y1，Y2，…，Ys)所携带的能量占总能量的比重大于α，则(1，2，…，s)是其占Yi的显著性水平为α 的s 个主元特征值，每个主元集中了各个分量的共同特征.另一方面，显然有X=PY.

根据前s 个主元的累计贡献率:

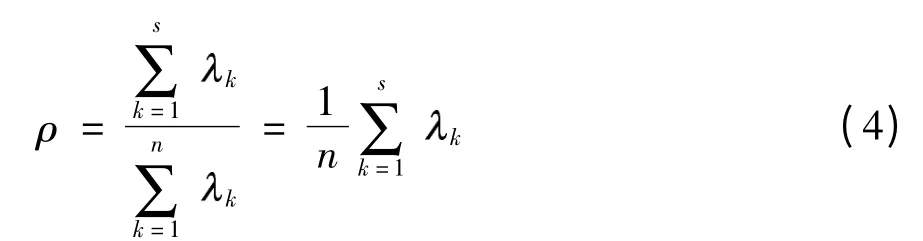
可确定s 个主元在整个诊断数据分析中承担的任务所占的比重，当取前s 个主元来代替原来全部变量时，累计贡献率的大小反应了这种取代的可靠性，累计贡献率越大，可靠性越大;反之，则可靠性越小.一般要求累计贡献率达到85%以上.

为使每个主元能正确反映对计算距离的影响程度，对主元特征数据标准化.标准化公式为

3 模糊模式识别

对大量强相关的多维数据降维处理、提取主元特征后，便可仅面向能量保持率最大的第一主元，运用核密度估计和最大熵原理确定最佳分类数和初始聚类中心，最后仅针对主元能量数据进行模糊聚类，得出最佳故障数据中心，通过计算待辨识模糊子集的最大贴近度，实现故障识别.

3.1 基于主元熵的最佳分类数的确定

信息熵是一种基于信息表现特征的统计形式，它反映了一组信息中平均信息量的多少［12］.主元熵描述了第一主元数据分布的聚集特征和相似程度，为总体平均不确定性的度量.熵越小，说明数据排列区间较大(聚类特征不明显);反之，则数据分布区间越小.聚类结果体现的最大主元熵所对应的分类数即为最佳分类数.

数据经主元特征提取后，第一主元的能量保持率最大，且相关系数最小，其已成为决定最佳分类数的最佳要素.设最佳分类数为l，可能最大分类数为M，即有1≤l≤M，采用普通一维K-均值算法进行聚类，求出各聚类子集的主元熵的平均值，即Ql=其中pj为第j 个分类子集中的数据Dj={xj1，xj2，…，xjn}的主元熵，有

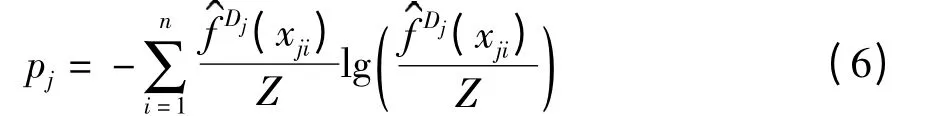
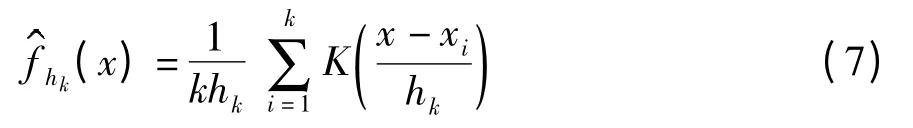
式中，K(·)为核函数，hk为带宽.文中采用高斯核函数，带宽选取按Silverman 拇指法则［13］，即

问题转化为非线性最大约束问题:

s.t.1≤l≤M.

至此，由最大熵确定了l 值，第一主元聚类中心也随之产生.将二者作为聚类算法所需的初始值，可有效避开随机选取初始值的敏感问题，提高算法的准确度及收敛速度.

3.2 聚类中心的确定

寻求聚类中心采用FKM 算法，其由k 均值算法派生而来［14］.其基本思想是首先设定分类数及每个样本对各类的隶属度，然后通过迭代，不断调整隶属度至收敛.收敛条件是隶属度的变化量小于规定的阈值.

设定聚类过程的目标函数Jm(U，V)为

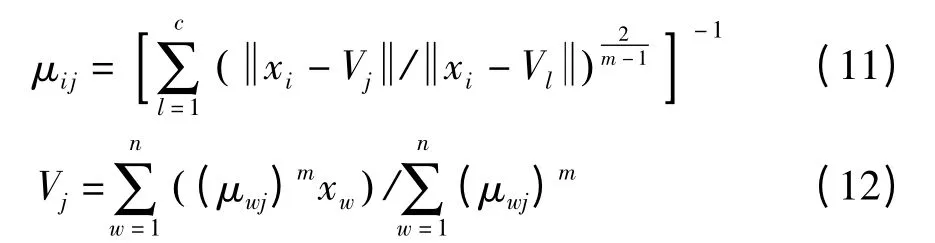
3.3 最大贴近度计算

在进行多维故障数据的模式识别时基于择近原则，即计算待辨识数据的主元特征值向量与标准聚类中心的最大贴近度以确认故障类别.给定论域U上的模糊子集(Vij)c×q，及另一模糊子集Sx，若有1≤i≤c，使得Nm(Sx，Vi)=(Sx，Vj)，则说明Sx与Vj最为贴近，属于模式Vj.有

式中，μS(ui)和μV(ui)分别为U 中元素ui对于Sx和Vj的隶属度.

4 实验及结果分析

为验证算法的有效性，以丰田1ZZ-FE 直列四缸1.8 L 发动机故障诊断实验台架为研究对象(如图1 所示)，对各种故障下的样本能量数据进行分类研究.发动机属于较复杂的机电设备，输入与输出关系难以精确描述，不确定性因素和信息较多，即二十余个传感器的外送数据相关度高，呈现多故障、关联故障等多种复杂形式［15］.发动机自身的能量数据是验证算法有效性的良好载体.

图1 发动机故障诊断实验台架Fig.1 Engine fault diagnosis test platform

根据此类发动机的运行特点，选取的典型故障类型分别为:进气歧管漏气(C1，属气路故障);发动机电控单元(ECU)异常(C2，导致空燃比等数据波动);机油滤清器阻塞(C3，属润滑系统故障);气门间隙异常(C4，属配气系统故障);喷油嘴阻塞(C5，属油路故障);选取的典型发动机运行能量参数分别为:转速(r/min);气缸压力(MPa);节气门开度(%)、氧传感器输出电压(V)、燃油压力(MPa)、喷油脉宽(ms)、燃油修正值(%).发动机正常怠速时各个参数值为:{720，0.91，4.6，0.5，0.25，2.2，4.1}.在此选取了5 种故障下多传感器的输出数据各20 组作为聚类样本.

4.1 主元降维与初始分类

样本数据标准化后，从主元降维后的帕累托图(即图2)可知，前3 个主元贡献超过85%，取前3 个最大特征根对应的所有正交归一化特征向量组成子空间投影P，将原始数据压缩为3 维主元矩阵.

从前3 主元能量数据散点图(即图3(a))可以看出，有2类数据具有明显的聚类倾向，其余数据较分散.从双主元能量数据散点图(即图3(b)、(c)、(d)所示)可以看出，第1 主元对数据聚类具有决定性影响.因此，针对其进行最大熵聚类，再计算得到可能分类数2-6 分别对应的信息熵:0.1036、0.2640、0.4596、0.6513、0.3654.可见应将主元能量数据分类数定为5.

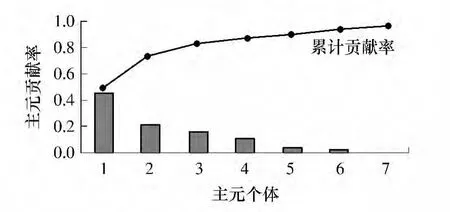
图2 帕累托图Fig.2 Pareto diagram

图3 主元能量数据散点图Fig.3 Diagram of principal component data

4.2 数据聚类与模式识别

经模糊聚类后，得到5 个聚类中心:

聚类效果如图4 所示，各聚类子集中所纳入的样本数量如表1 第2 列所示，平均准确率达到了96%，可见文中算法对高维数据的分类具有明显作用.

为进一步验证算法的有效性，针对同一组数据运用k 均值算法进行聚类分析，并与文中提出的算法各执行20 次，平均计算结果的对比信息见表2.算法运行环境为:Intel Croe2 CPU(2.93GHz)，4G 内存.由于k 均值算法的分类数以及初始聚类中心都是随机选择，聚类结果会呈现多样性.当初始中心选择不合理时，会导致算法的边界区域对象数目较多，甚至会造成某类下近似集为空，即产生一致性聚类，降低聚类准确度.

图4 主元能量数据聚类效果图Fig.4 Clustering diagram of principal component data

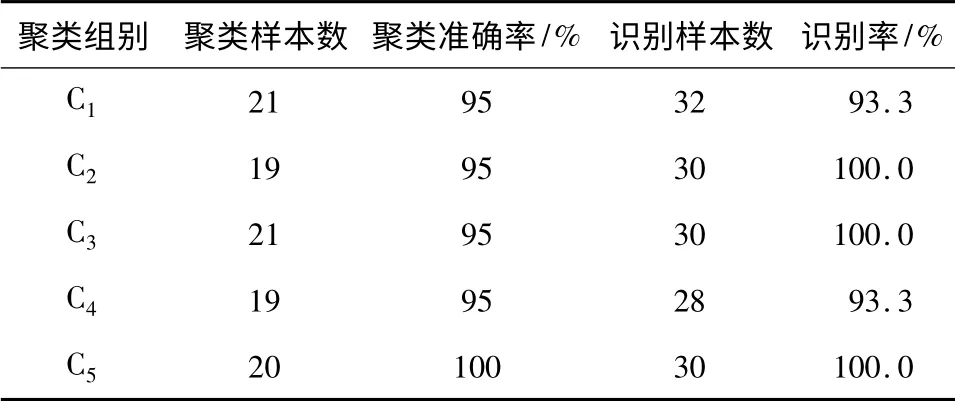
表1 数据聚类及识别结果Table 1 Results of data clustering and recognition

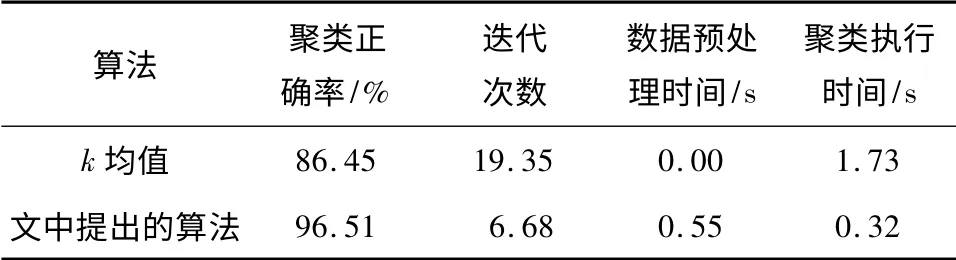
表2 两种聚类算法性能对比Table 2 Performance comparison of two clustering algorithms

为达到分辨不同故障信号的目的，另采集5 种故障模式下各30 组数据作为待测样本B，进一步对故障进行诊断识别.首先提取样本B 的主元特征并进行标准化处理，再利用模糊聚类形成的标准模型库，通过模糊识别进行目标故障模式匹配.从表1 中后2 列可看出，样本识别结果与实际基本一致，只有类型C1与C4因同属于气路故障导致数据贴近度均较大、聚类中心欧氏距离较小，故障4 中的2 组数据落入故障1 模式中，识别率较其他有所降低.

5 结语

文中提出了立足于数据降维以减少运算量，同时基于数据子集中数据趋同所反映出的信息熵最大化原理，先对第一主元能量数据聚类以获取最佳分类数和初始聚类中心，再执行聚类，显著提高了故障数据的聚类效果.同时，相对于神经网络、支持向量机等故障识别方法，文中提出的基于主元熵的模糊模式识别方法可快速形成模糊聚类中心，并通过最大贴近度建立故障识别规则，进一步提高了在小样本环境下，数据分布不清晰时的识别能力，具有识别快速、规则简洁、信息利用充分的特点.

［1］Lo C H，Fung E H K，Wong Y K.Intelligent automatic fault detection for actuator failures in aircraft［J］.IEEE Transactions on Industrial Informatics，2009，5(1):50-55.

［2］Basir O，Yuan X H.Engine fault diagnosis based on multisensor information fusion using Dempster-Shafer evidence theory［J］.Information Fusion，2007，8(4):379-386.

［3］Tang X L，Zhuang L，Cai J，et al.Multi-fault classification based on support vector machine trained by chaos particle swarm optimization ［J］.Knowledge-Based Systems，2010，23(5):486-490.

［4］孙宜权，张堂英，李志伟.基于Kalman 转移矩阵的发动机故障诊断方法［J］.噪声与振动控制，2012，32(5):159-163.Sun Yi-quan，Zhang Tang-ying，Li Zhi-wei.Method of engine fault diagnosis based on Kalman matrix［J］.Noise and Vibration Control，2012，32(5):159-163.

［5］王彦岩，杨建国，宋宝玉.基于小波和模糊C-均值聚类算法的汽油机爆震诊断研究［J］.内燃机工程，2011，32(4):56-59，64.Wang Yan-yan，Yang Jian-guo，Song Bao-yu.Study on gasoline engine knock diagnosis based on wavelet transform and fuzzy C-means clustering［J］.Internal Combustion Engine Engineering，2011，32(4):56-59，64.

［6］Rolf Isermann.Model-based fault-detection and diagnosisstatus and applications［J］.Annual Reviews in Control，2005，29(1):71-85.

［7］Naresh R，Sharma V，Vashisth M.An integrated neural fuzzy approach for fault diagnosis of transformers ［J］.IEEE Transactions on Power Delivery，2008，23(4):2017-2024.

［8］张淑清，孙国秀，李亮，等.基于LMD 近似熵和FCM 聚类的机械故障诊断研究［J］.仪器仪表学报，2013，34(3):714-720.Zhang Shu-qing，Sun Guo-xiu，Li Liang，et al.Study on mechanical fault diagnosis method based on LMD approximate entropy and fuzzy C-means clustering［J］.Chinese Journal of Scientific Instrument，2013，34(3):714-720.

［9］孙吉贵，刘杰，赵连宇.聚类算法研究［J］.软件学报，2008，19(1):48-61.Sun Ji-gui，Liu Jie，Zhao Lian-yu.Clustering algorithms research［J］.Journal of Software，2008，19(1):48-61.

［10］谢小鹏，肖海兵，冯伟，等.基于局部线性嵌入的能量耗损故障模式识别［J］.华南理工大学学报:自然科学版，2012，40(12):1-6.Xie Xiao-peng，Xiao Hai-bing，Feng Wei，et al.Fault pattern recognition of energy loss based on locally linear embedding ［J］.Journal of South China University of Technology:Natural Science Edition，2012，40(12):1-6.

［11］Zhang L，Dong W S，Zhang D，et al.Two-stage image denoising by principal component analysis with local pixel grouping［J］.Pattern Recognition，2010，43(4):1531-1549.

［12］王毅，雷英杰.一种直觉模糊熵的构造方法［J］.控制与决策，2007，22(12):1390-1394.Wang Yi，Lei Ying-jie.A technique for constructing intuitionstic fuzzy entropy［J］.Control and Decision，2007，22(12):1390-1394.

［13］Yu J，Yang M S.Optimality test for generalized FCM and its application to parameter selection ［J］.IEEE Transactions on Fuzzy Systems，2005，13(1):164-176.

［14］Kang S，Ryu J，Lee J，et al.Analysis of space-time adaptive processing performance using K-means clustering algorithm for normalisation method in non-homogeneity detector process［J］.IET Signal Processing，2011，5(2):113-120.

［15］谢小鹏，肖海兵，冯伟.基于能量耗损的发动机故障诊断方法研究［J］.润滑与密封，2011，36(5):1-3，58.Xie Xiao-peng，Xiao Hai-bing，Feng Wei.Study on the method of engine fault diagnosis based on energy loss［J］.Lubrication Engineering，2011，36(5):1-3，58.