内置悬置轮毂电机驱动系统参数灵敏度分析*

谭迪 罗玉涛 叶志伟

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

轮毂电机驱动电动汽车作为下一代电动汽车的关键技术之一，在底盘结构布置、驱动方式等方面均与集中电机驱动车辆有很大不同［1-4］.其将电机、减速机构等集成于车轮内，这种高度集成使其在主动安全集成控制、整车空间布置、节能环保等方面具有明显的技术优势，但也使车辆非簧载质量增加，同时，来自路面的激励还会造成电机气隙不均匀现象的产生，导致轮毂电机引起的振动激励进一步恶化，给车辆的平顺性和接地安全性带来不利影响.

由于轮毂电机驱动电动汽车的研发尚处于起步阶段，以上问题尚未引起普遍的关注.文献［5-6］指出，由于轮毂电机的引入，整车的非簧载质量明显增加，使轮胎动载和车身的振动加速度均方值都明显增大.文献［7-8］通过特殊平面电机设计，将电机的定子质量转化为簧载质量对轮边驱动系统进行设计.文献［9］通过特殊形式电机将非簧载质量转化为簧载质量，从而减小非簧载质量带来的负面效应.文献［10］利用电机质量构造吸振器对非簧载质量引发的垂向振动负效应进行控制.文献［11］以双横臂扭杆弹簧被动悬架和主动悬架模型对车辆非簧载质量过大引起的垂向振动负效应进行了分析.文献［12］提出通过设置与悬架系统并联的减振机构将轮毂电机定子质量由簧下质量转化为簧上质量，但这种布置形式将使定转子的相对动挠度增大，引起电机气隙磁场分布不均，进而导致一系列动力学问题的产生.文献［13-14］则针对前述轮毂电机等引入车轮导致非簧载质量增加和电机气隙不均匀的问题，提出了一种内置悬置的轮毂电机驱动系统，其通过设置悬置元件，将轮毂电机作为一个整体与簧下质量进行弹性隔离，再将电机转化为与簧上质量并联的质量，从而提高簧上和簧下质量比值，同时尽量减小来自路面的激励对电机气隙的影响;文献［13-14］中，有、无悬置两种电动轮方案的仿真对比分析表明:设置悬置后，车辆在车身加速度、轮胎动载荷、悬架动行程及定转子相对位移等方面均有不同程度的改善，尤其是对定转子的相对位移量的改善最为显著;悬置元件的设置在改善车辆垂向动力学性能方面具有一定效果.

在前期工作的基础上，文中对内置悬置轮毂电机驱动系统参数灵敏度进行详细分析.具体如下:①建立考虑轴承刚度的1/4 车辆模型;②根据模型，推导多质量系统车身加速度、车轮相对动载、悬架动挠度及定转子相对位移量等各振动响应量对路面不平度速度输入的频响函数;③分析各振动响应量对电机质量、定转子质量比、轴承刚度、悬置元件刚度和阻尼等重要结构参数的灵敏度，分析系统参数对振动响应的影响规律.

1 内置悬置轮毂电机驱动系统模型

图1 所示为新型内置悬置系统电动轮拓扑结构［13-14］.忽略轴承内部径向游隙的影响，不考虑润滑油膜的作用，在垂向将轴承和橡胶衬套等效为弹簧-阻尼器，得到车辆的1/4 模型，如图2 所示.

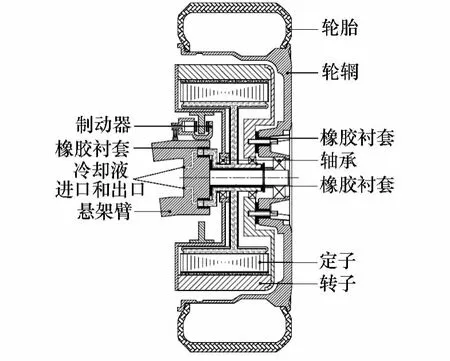
图1 新型内置悬置系统电动轮结构原理图［13-14］Fig.1 Sketch of a novel in-wheel motor system with mounting component［13-14］

图2 新型结构车辆1/4 模型Fig.2 Quarter vehicle model of the novel structure

利用图2 中1/4 模型，得到系统振动微分方程:

式中:m1为非簧载质量，m2为簧载质量，m31为支承轴、制动钳等质量，m32为定子质量，m33为转子及制动盘质量;y0为路面不平度位移输入，yl为相应质量块的位移，l=1，2，31，32，33;ki和ci分别表示轮胎、悬架、衬套、轴承的刚度和阻尼，其中i=1，2，31，32，41，42.

2 多质量系统幅频特性

在无阻尼自由振动时，设各质量以相同的圆频率ω 和相位角φ 作简谐振动，振幅为y10、y20、y310、y320、y330，则其解为y1= y10ej(ωt+φ)，y2= y20ej(ωt+φ)，y31=y310ej(ωt+φ)，y32=y320ej(ωt+φ)，y33=y330ej(ωt+φ).其中，t 为时间变量.

将各复振幅代入式(1)，可得到多质量系统各频率响应函数为其中:

A32=-ω2m32+jω(c31+c42)+(k31+k42);

A33=-ω2m33+jω(c32+c42)+(k32+k42).

式中:Fd和D 分别为车轮作用于路面的动载荷和静载荷，g 为重力加速度，mt为汽车静止时路面承受的车辆质量.

3 路面随机输入下系统振动响应均方根值的计算

3.1 随机路面模型

作为车辆振动输入的路面不平度，路面垂直位移功率谱密度Gq(n)的表达式为

式中:n 为空间频率;n0为参考空间频率，n0=0.1 m-1;Gq(n0)为参考空间频率n0下的路面功率谱密度值，称为路面不平度系数;w 为频率指数.

当车辆以一定车速u 驶过空间频率n 的路面不平度时输入的时间频率 =un .由此，某一车速u 下的功率谱进行换算得到两者的关系如下:

由此可得到w=2 时的时间频率路面谱密度为

时间频率的不平度垂直速度˙q(t)=dq(t)/dt 的功率谱密度G˙q()与位移功率谱Gq()的关系式为

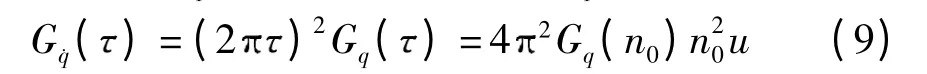
3.2 振动响应均方根值的计算

求出各振动响应量的幅频特性，并计算得到G˙q().由式(10)即可求出各响应量的功率谱密度.

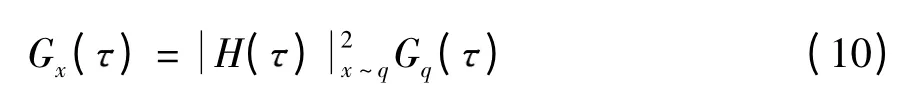
此值可由其功率谱密度对频率积分求得，以车身加速度为例，其均方值为

将式(9)的路面功率谱密度代入式(11)，得

式(12)中幅频特性的表达式相当复杂，一般难以用解析的方法直接进行积分，在工程上采用数值积分的方法.等间隔取r 个离散频率值，频带宽度为Δ，则式(12)变为

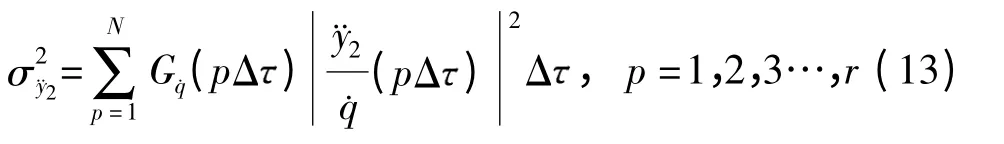
4 振动响应对系统参数的灵敏度分析

为分析车身与电机质量比B1= m2/(m32+m33)、质量比B2=m32/m33、轮毂轴承与轮胎刚度比B3=k41/k1、轮胎与悬置元件刚度比B4=k1/k31及悬架与悬置元件阻尼比B5=c2/c31这5 个参数对振动响应、fd、ε、Fd/D 的影响，采用上述数值积分方法计算了B 级路面下，车速u =20 m/s 时，4 个响应量、fd、ε、Fd/D 的均方根值σ¨y2、σfd、σε、σFd/D，计算时带宽Δ 取0.5 Hz，计算上限频率为300 Hz.为将响应量均方根值的变化在同一幅图中表示，将σ¨y2、σfd、σε、σFd/D做如下处理:

在分析系统某参数对振动响应量的影响时，将其基准数值增大100%(+6 dB)或减小50%(-6 dB)，其余3 个参数保持不变.表1 和表2 分别为车辆参数基准值及灵敏度分析参数取值.

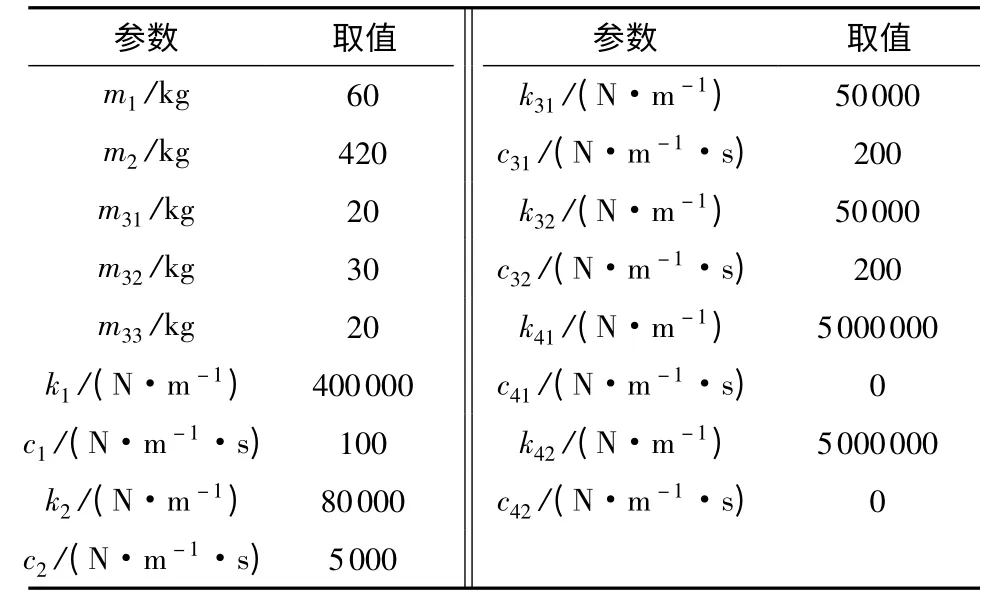
表1 车辆参数Table 1 Parameters of vehicle model

表2 系统参数取值Table 2 Values of system parameters

4.1 车身与电机质量比B1 的影响

B1为4.2、8.4、16.8，其他参数保持不变时，、Fd/D、fd、ε 对˙y0的幅频特性见图3(a)，根据B1为3 种取值时各响应量均方根的归一值，得到一定范围内各振动响应量归一值的拟合曲线，如图3(b)所示.仿真过程中，只改变电机定转子总质量(m32+m33)，m2及质量比m32/m33均保持不变.

图3 B1 对、fd、ε、Fd/D 的影响Fig.3 Influence of B1 on 、fd、ε、Fd/D

由图3(a)可以看出，随着B1的增大，各振动量幅频特性的第2 个和第3 个共振峰值明显向后推移，且第2 个向后推移较大，说明系统第二、三阶固有频率受电机总质量影响，随其减小而增大;且在二、三阶共振频率间各响应量明显下降.

由图3(b)可知，车身加速度、悬架动行程、定转子相对位移量及轮胎相对动载荷的均方根归一值σ1、σ2、σ3、σ4均随B1的增大而减小，由此可见，车身质量一定的情况下，电机的总质量越小，各响应量均有所减小，对B1的敏感程度由强到弱依次为:

4.2 质量比B2 的影响

B2为0.75、1.50、3.00，其他参数保持不变时，、fd、ε、Fd/D 对˙y0的幅频特性见图4(a)，一定范围内各振动响应量归一值的拟合曲线见图4(b).仿真过程中，改变电机定、转子质量m32和m33的比值，但总质量(m32+m33)保持不变.

由图4(a)可以看出，B2对4 个振动响应量的幅频特性影响不大，只是在高共振频率附近产生较大波动，对悬架动行程产生一定影响.

由图4(b)可知:σ3、σ4随B2的增大而减小，σ1、σ2则随B2的增大而增大.由此可见，在电机总质量一定的条件下，m32/m33值增大对定转子相对位移和轮胎动行程产生有利作用，但同时使车身加速度和悬架动行程有所增加.各振动量对B2的敏感程度由强到弱依次为

4.3 刚度比B3 的影响

B3为6.25、12.50、25.00，k41=k42，而其他参数保持不变时，各响应变量的幅频特性见图5(a)，一定范围内各振动响应量归一值的拟合曲线见图5(b).仿真中，保持轮胎刚度k1值不变，只改变k41、k42的取值.

由图5(a)可知，随着B3增大，各振动量高频共振峰值向后推移，高频共振区的振动幅值有所下降，系统后两个高阶固有频率随B3的增大而增大;同时，随着B3的增大，、Fd/D、fd对˙y0的幅频特性在最后一个共振峰后，沿相同的斜率方向向右下方平移的移动量最小，而ε 对˙y0的幅频特性在第3 个共振峰前沿相同斜率方向向下平移，在第3 个共振峰后，则以越来越小的斜率向右下方移动.

图4 B2 对、Fd/D、fd、ε 的影响Fig.4 Influence of B2 on 、Fd/D、fd、ε

由图5(b)可知σ3随B3的增大而减小，轴承刚度越大，定转子的相对位移量越小;其余振动量均随B3的增大而增大，但变化幅度较小;σ3对B3的变化最为敏感.各振动量对B3的敏感程度由强到弱依次为:

4.4 刚度比B4 的影响

B4为4、8、16，k31=k32，其他参数保持不变时，、fd、ε、Fd/D 对˙y0的幅频特性见图6(a)，一定范围内各振动响应量归一值的拟合曲线见图6(b).仿真中，保持k1不变，只改变k31、k32取值.

图5 B3 对、Fd/D、fd、ε 的影响Fig.5 Influence of B3 on 、Fd/D、fd、ε

由图6(a)可以看出，随着B4的增大，各振动量的第二、三阶共振峰向前移动，共振峰值有所减小，说明B4的取值影响系统二、三阶固有频率，B4越大，第二、三阶固有频率越小.

由图6(b)可知，σ3、σ4随B4的增大而增大，σ1、σ2则随B4的增大先减后增，σ1、σ2变化趋势基本相同.由此可见，从轮胎动载和定转子相对位移量的要求来说，悬置系统刚度应越小越好，但对于车身加速度和悬架动行程，存在某一最优刚度使两指标达到性能最优，刚度过大或过小，σ1、σ2均呈上升趋势.由图得到各振动量对B4的敏感程度由强到弱依次为:

图6 B4 对、Fd/D、fd、ε 的影响Fig.6 Influence of B4 on 、Fd/D、fd、ε

4.5 阻尼比B5 的影响

B5为12.5、25.0、50.0，c31=c32，c2及其他参数保持不变时，、Fd/D、fd、ε 对˙y0的幅频特性见图7(a)，一定范围内各振动响应量归一值的拟合曲线见图7(b).仿真中，只改变轴承刚度c31的取值.

由图7(a)可见，随着阻尼比B5的增大，在二、三阶共振区幅频特性的峰值均有所上升;而在二、三阶共振区之间幅值有明显下降则有所上升变化很小.

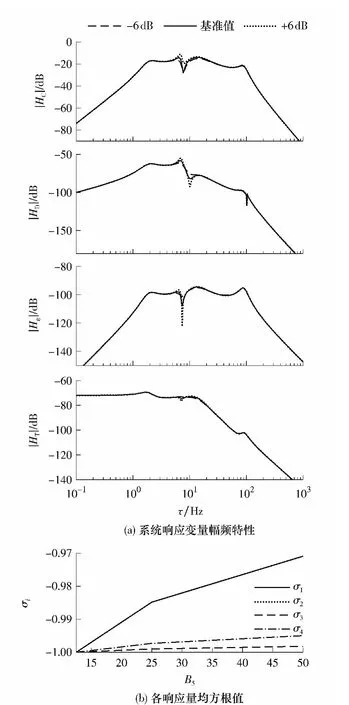
图7 B5 对、Fd/D、fd、ε 的影响Fig.7 Influence of B5 on 、Fd/D、fd、ε

由图7(b)可知，随着B5的增大，振动量均呈增大趋势，各振动量对B5的敏感程度由强到弱依次为:由此可见，悬架阻尼c2不变的情况下，悬置元件的阻尼c31、c32越大越好.

4.6 振动响应灵敏度

在4.1 至4.5 节分析各系统参数对振动响应量影响趋势的基础上，本节采用扰动法进行灵敏度计算，表达式如下:

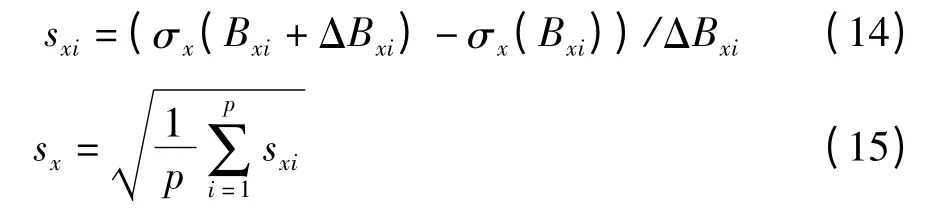
式中，i 为各参数设计区间分段数，ΔBxi为系统参数x 在区间i 内的增量值，sx为各振动量对各系统参数的响应灵敏度.

利用4.1 至4.5 节对表2 中各组参数下振动响应量均方根值的计算结果，利用式(14)、(15)得到各振动响应灵敏度的统计值，见表3.

表3 振动响应灵敏度Table 3 Sensitivity of vibration response

由表3 可知:对车身振动加速度和悬架动行程影响最大的均为悬置元件的阻尼B5，其灵敏度分别达到10.33 和10.21，且这两个振动响应量对其他参数的敏感度强弱排序均为B1、B4、B3、B2;而定转子间的相对位移量则对轮毂轴承刚度B3最为敏感，其敏感度达到12.07，对其他参数敏感度强弱依次为B5、B4、B1、B2;轮胎动载荷则对电机总质量B1最为敏感，其敏感度为10.49，对其他参数敏感度强弱依次为B4、B5、B3、B2;且综合各个参数来看，电机定转子的质量比B2对各振动响应量的影响均较小.

5 结论

文中以一种内置悬置轮毂电机驱动系统为研究对象，分析了车身加速度、悬架动行程、定转子相对位移量及轮胎相对动载等振动响应量对电机质量、定转子质量比、轴承刚度、悬置元件刚度及阻尼等系统重要结构参数的灵敏度，结果表明:

(1)悬置元件的阻尼对车身振动加速度和悬架动行程影响最大，其灵敏度分别达到10.33 和10.21，且两者对其他参数的敏感度强弱均依次为B1、B4、B3、B2，且悬置元件的阻尼越大，各振动响应量越小.

(2)定转子的相对位移量对轮毂轴承刚度最为敏感，其敏感度达到12.07，对其他参数敏感度强弱依次为B5、B4、B1、B2，且轴承刚度越大，定转子的相对位移量越小，而其余振动量则随轴承刚度的增大而增大，但变化幅度相对较小.

(3)轮胎相对动载对电机总质量最为敏感，其敏感度为10.49，对其他参数敏感度依次为B4、B5、B3、B2，车身质量一定的情况下，电机的总质量越小，各振动响应量越小.

(4)综合各个参数来看，电机定转子的质量比B2对各振动响应量的影响均较小.

本研究为后续系统参数控制和优化奠定基础的同时对轮毂驱动汽车减振技术的研究有重要意义.

［1］Li X H，Qian H.The present status and future trends of in-wheel motors for electric vehicles［J］.Advanced Materials Research，2012(433/434/435/436/437/438/439/440):6943-6950.

［2］Hori Y.Future vehicle driven by electricity and controlresearch on four wheel-motored“UOT Electric March II”［J］.IEEE Transactions on Industrial Electronics，2004，51(5):954-962.

［3］Yoshimura Masataka，Fujimoto Hiroshi.Driving torque control method for electric vehicle with in-wheel motors［J］.Electrical Engineering in Japan，2012，181(3):49-58.

［4］罗玉涛，旷鹏，刘延伟.对转双转子电机在电动汽车上的驱动特性［J］.华南理工大学学报:自然科学版，2008，36(2):7-12.Luo Yu-tao，Kuang Peng，Liu Yan-wei.Driving performance of anti-direction dual-rotor motor for electric vehicle［J］.Journal of South China University of Technology:Natural Science Edition，2008，36(2):7-12.

［5］Purdy D J，Simmer D.A brief investigation into the effect on suspension motions of high unsprung mass［J］.Journal of Battlefield Technology，2004，7(1):15-20.

［6］Siddiqui O M.Dynamic analysis of a modern urban bus for assessment of ride quality and dynamic wheel loads［D］.Montreal:The Department of Mechanical Engineering，Concordia University，2000.

［7］Johansen P R，Pattersib D，O’keefe C.The use of an axial flux permanent magnet in-wheel direct drive in an electric bicycle［J］.Renewable Energy，2001，22(1/2/3):151-157.

［8］Yang Y P，Luh Y P，Cheung C H.Design and control of axial-flux brushless DC wheel motors for electric vehicles-part I:multi-objective optimal design and analysis ［J］.IEEE Transactions on Magnetics，2004，40(4):1873-1882.

［9］Eastham J F，Balchin M J，Becter T，et al.Disk motor with reduced unspring mass for direct EV wheel drive［C］∥Proceedings of the IEEE International Symposium on Industrial Electronics.Athens:IEEE，1995:569-573.

［10］Nagaya G，Wakao Y，Abe A.Development of an in-wheel drive with advanced dynamic-damper mechanism ［J］.JSAE Review，2003，24(4):477-481.

［11］夏存良，宁国宝.轮边驱动电动车大质量电动轮垂向振动负效应主动控制［J］.中国工程机械学报，2006，4(1):31-34，42.Xia Cun-liang，Ning Guo-bao.Active control of vertical vibration negative influences induced by high unsprung mass of in-wheel motor electric vehicle ［J］.Chinese Journal of Construction Machinery，2006，4(1):31-34，42.

［12］赵艳娥，张建武，韩旭.轮毂电机独立驱动电动汽车动力减振机构设计与研究［J］.机械科学与技术，2008，27(3):395-398，404.Zhao Yan-e，Zhang Jian-wu，Han Xu.Design and study on the dynamic-damper mechanism for an in-wheel motor individual drive electric vehicle［J］.Mechanical Science and Technology for Aerospace Engineering，2008，27(3):395-398，404.

［13］罗玉涛.一种内置悬置集成式轮毂电机驱动电动轮:中国，201210018416.7［P］.2012-09-19.

［14］Luo Yutao，Tan Di.Study on the dynamics of the inwheel motor system［J］.IEEE Transactions on Vehicular Technology，2012，61(8):3510-3518.