大口径天线伺服系统的建模及控制算法设计*

张磊 廖鑫江

(华南理工大学 自动化科学与工程学院，广东 广州 510640)

大口径射电望远镜天线可以接收和发送射电波信号，主要应用于射电天文观测和深空探测.指向精度作为射电望远镜天线的一项主要性能指标，其优劣不仅影响到射电望远镜发现和观测目标的能力，还会影响天线伺服系统的跟踪性能.随着对信号接收质量要求的不断提高，射电望远镜天线的口径不断地向大型化趋势发展［1］.为了提高数据的传输速率，天线的工作频率越来越高，美国NASA 深空网天线的工作频率从S 频段(4 GHz)和X 频段(8 GHz)发展到Ka 频段(32 GHz)，且Ka 频段的跟踪精度要求达到0.002°.大型毫米波望远镜天线甚至工作在200 GHz 的频率以获得超高的指向精度，这些高指向精度要求给天线控制工程师带来了前所未有的挑战［2］.为了提高天线伺服系统的响应速度、稳态精度和指向精度等性能指标，需要提高伺服系统的带宽.然而在实际工程中，阻碍天线伺服系统带宽提高的主要因素是天线结构的高频谐振，这些高频谐振同时也会影响天线伺服系统的稳定性.传统的PID控制算法虽然能够满足小型刚体天线系统的指标要求，但对大口径天线系统的作用效果欠佳，主要原因是大口径天线存在柔性结构高频谐振模态，PID 控制在提高系统的带宽时也会提高系统的高频增益，激励出系统的高频谐振不确定性，影响伺服系统的性能指标和稳定性.先进的控制算法设计越来越成为天线伺服控制研究人员和天线控制工程师的兴趣所在.文献［3-8］将基于扰动观测器的鲁棒自适应控制、线性二次高斯(LQG)控制、H_infinity 控制、预测控制和自抗扰控制等先进的控制算法引入高精度伺服控制系统，以提高系统的带宽和伺服性能.

天线伺服控制系统主要包括系统建模和控制算法设计两个部分.系统建模对控制算法的设计十分重要，特别是基于模型的控制算法设计如LQG 控制和H_infinity 控制等.文献［2］研究了通过开环辨识方法建立天线伺服系统的模型.天线在实际运行过程中，最主要的外界扰动是风，风作用在天线的反射面结构上会影响系统的稳定性和指向精度.文中首先介绍天线控制系统的结构，然后建立伺服系统的模型，针对传统的PID 控制不能满足大口径天线伺服系统的性能指标要求的情况，设计了一种混合灵敏度H_infinity 控制算法，最后通过仿真研究验证了天线伺服系统的性能指标.

1 控制系统结构

天线主要围绕垂直轴和水平轴分别进行方位运动和俯仰运动，且方位运动和俯仰运动是相互独立的.为了简便起见，此处仅考虑一个方向的运动.天线控制系统由速度环和位置环组成，如图1 所示.图中r 表示给定信号，T 表示转矩，d 表示外界扰动，ω表示天线的角速度，y 表示天线的角位置输出.文中某大口径天线要求的角速度运动范围为0～0.5°/s，角加速度运动范围为0～0.25°/s2.实际工程中，在速度给定较大的情况下，天线的驱动容易发生过载或损坏，为了防止这种现象，通常在控制回路中加入一个保护装置［9］，例如速度限制器或者抗饱和装置等，以保证天线的角速度和角加速度工作在正常的运动范围内.

图1 天线控制系统Fig.1 Antenna control system

2 系统建模

2.1 电机驱动模型

天线伺服系统的电机驱动模型(不考虑负载时)如图2 所示，其中，Va表示电枢电压，Ra表示电枢回路的等效电阻，La表示电感，Ia为电枢电流，Tm为电机的转矩，ωm为电机轴的角速度，θm为电机轴的角位置.电枢回路中各物理量之间满足

图2 电机驱动模型Fig.2 Motor drive model

式中:E 表示电机的反电动势，he表示反电动势系数，Jm为电机的转动惯量，fm为电机的转矩系数.

从电枢电压Va到电机轴的角速度ωm的传递函数为

式中:s 为复变量，a=La/Ra，m=JmRa/(fmhe).

电枢回路的电感La一般很小，可以忽略不计，记km=1/he，电机的数学模型可以近似为［10］

2.2 速度环模型

天线伺服系统的速度环开环模型包括天线的结构和驱动模型.速度环模型可以通过开环现场测试方法得到［2］.大口径天线系统存在许多柔性结构高频谐振模态，这些高频谐振模态可以表示为系统的高频未建模动态不确定性.天线伺服系统的速度环模型G(s)可以表示为

式中，k 为开环增益，为时间常数，i 为第i 个高频谐振模态;ωi为高频谐振模态的谐振频率，ζi为谐振模态的阻尼系数，ci为谐振模态的增益.

在实际工程中，一般只考虑前几个高频谐振模态.某大口径天线的前4 个高频谐振模态的频率分别为:6.4、7.4、8.7、12.4 rad/s.谐振模态的阻尼系数不能通过开环现场测试得到精确值，只能估计出其取值范围，阻尼系数取值范围为0.01≤ζi≤0.20.某大口径天线伺服系统的开环频率响应如图3 所示，从频率响应可以看出，天线伺服系统存在4 个高频谐振峰，这些谐振峰会阻碍系统带宽的提高，影响天线系统的伺服性能和稳定性.

2.3 风扰动模型

大口径天线一般工作在比较空旷的地方，因此会受到不同方向的风的干扰作用.风作用在天线的反射面结构上会影响系统的稳定性和指向精度.由于风速和风向的变化，风扰动可以建模为稳态风和阵风两个部分.稳态风的模型可以通过风洞试验得到［11］，而阵风的模型主要通过风力、风转矩和风速等3 种方法建模［12］.文中考虑将风扰动建模成一个作用在天线面板结构上的时变转矩［13］.

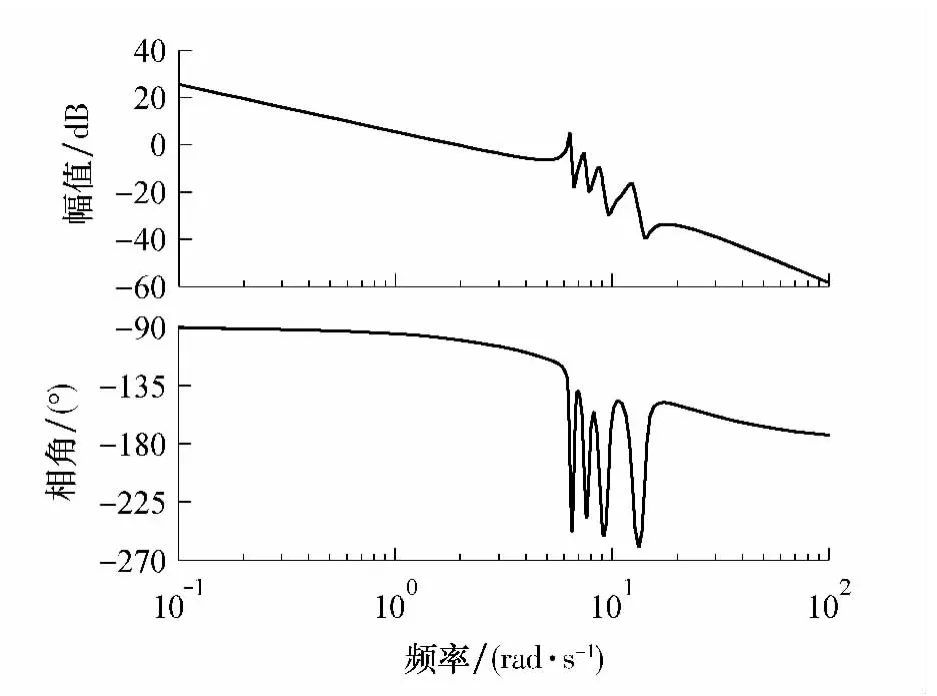
图3 开环频率响应Fig.3 Frequency response of open-loop system

风速v 由稳态风速vs和阵风风速Δv 两个部分组成，即v=vs+Δv.阵风可以表示为一个均值为零、功率谱密度为Davenport 谱的随机过程.Davenport谱密度记为φv(ωH)，与平均风速和地形粗糙度有关，表示为

其中ωH为角频率，α =600/( vs).为表面阻力系数，由地形粗糙度决定:

式中，l 为天线反射面中心离地面的距离，l0为地形粗糙度的高度.

由稳态风速vs产生的转矩Ts可以表示为

其中ks为转矩系数，与天线的结构、方位角、俯仰角、地形和风向有关［13］，且

式中:β 为无量纲的转矩系数，与风向和天线的俯仰位置有关;σp为静态空气密度;A 为天线反射面板的面积;D 表示天线反射面板的直径.

阵风会产生一个时变转矩，由于阵风的风速一般是稳态风速的10%～20%，可以根据式(7)线性近似得到阵风的时变转矩.通过对式(7)两边取微分可以得到天线的轴转矩

阵风转矩Tw(t)可以表示为轴转矩ΔTs除以轴齿轮比N，即

阵风产生的时变转矩和阵风风速之间满足线性关系，比例系数为

因此阵风模型可以建模为:一个白噪声信号n经过一个Davenport 滤波器得到阵风风速Δv，然后乘以一个比例系数kw得到时变转矩Tw.

3 控制算法设计

针对大口径天线伺服系统同时存在柔性结构高频谐振和低频风扰动的问题，文中考虑同时设计传统控制算法和先进控制算法来提高伺服系统的带宽.文中采用了PID 控制算法和混合灵敏度H_infinity控制算法，并通过仿真比较了两种控制算法对天线伺服系统的性能改善作用.

3.1 PID 控制

PID 控制主要由比例单元、积分单元和微分单元3 个部分组成，其中比例系数kp、积分系数ki和微分系数kd为可设计参数.图4 为PID 控制的结构图，其中e 表示伺服误差，u 表示控制信号.

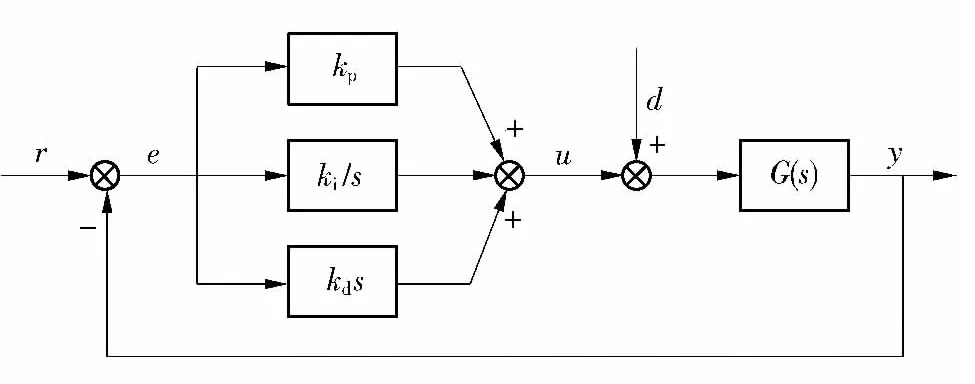
图4 PID 控制结构图Fig.4 Structure diagram of PID control

对于低阶被控对象，PID 控制可以提高伺服系统的快速性，缩短系统的调节时间，并提高系统的稳态精度.但PID 控制对高阶被控对象的高频段频率特性的补偿能力非常有限，而且对系统的稳态裕量等品质的改善效果欠佳.当被控对象为小型刚体天线时，采用PID 控制并适当地调节kp、ki和kd，可以在一定范围内提高天线伺服系统的带宽和稳定裕量，以达到不同的设计要求.然而大口径天线系统存在柔性结构高频谐振等不确定性，系统的性能会受到较大的影响.主要原因在于:PID 控制在提高系统带宽时所采用的增大kp或者kd的方法都会提高系统的高频增益，这可能会进一步激励系统的高频不确定性.在这类情况下，必须要调小kp或者kd，以牺牲系统的动态响应速度为代价来抑制高频不确定性.当系统同时存在外界低频风扰动时，情况更为复杂.

3.2 混合灵敏度H_infinity 控制

3.2.1 混合灵敏度设计

考虑一个单输入单输出线性时不变系统，系统的输入和输出之间的关系可以用传递函数G(s)表示，或者用下列状态空间模型表示.

式中:x 表示系统的状态，x∈Rn;u 表示控制信号，u∈R;y 表示系统的输出，y∈R.系统矩阵A∈Rn×n，B∈Rn×1，C∈R1×n，D∈R.图5 为系统的混合灵敏度设计框图，其中K(s)表示控制器，W1(s)、W2(s)和W3(s)表示权重函数，z1、z2和z3表示权重输出.

图5 混合灵敏度设计Fig.5 Mixed-sensitivity design

系统的灵敏度函数S(s)定义为

相应的补灵敏度函数M(s)定义为

系统反馈控制的目标是设计一个镇定控制器K(s)使得闭环系统混合灵敏度函数的H_infinity 范数最小，即使得性能指标最小:

在实际中一般通过迭代法寻找一个次优的控制器K(s)，使得对于一个给定的任意小的参数γ，系统混合灵敏度函数的H_infinity 范数满足

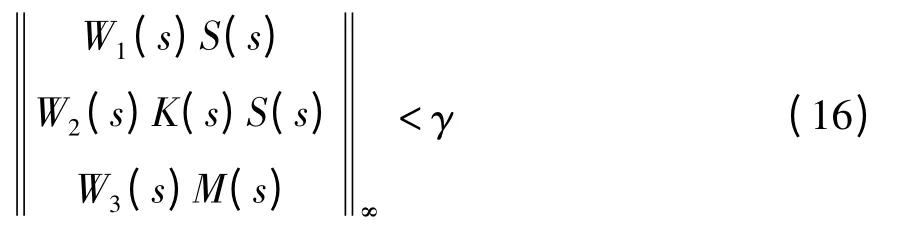
3.2.2 权重函数的选择

权重函数W1(s)、W2(s)和W3(s)的选择在混合灵敏度设计中起到十分重要的作用［14］.W1(s)是系统跟踪误差的惩罚函数，一般选择W1(s)为一个低通滤波器.W2(s)反映控制信号的大小和带宽，同时W2(s)的设计要防止出现执行器的饱和及不稳定的控制器.W3(s)决定系统高频特性的衰减程度，为减少控制器的阶数，W3(s)设计为一个常数.混合灵敏度函数的整形问题可以反映整个系统的伺服性能，系统混合灵敏度函数的H_infinity 范数越小，意味着闭环系统的跟踪误差越小，控制信号越小，稳定裕量越大［15］.

3.2.3 带宽约束

设计反馈控制器使得系统混合灵敏度函数的H_infinity范数最小的目的是尽可能地提高闭环系统的带宽.闭环系统的带宽越高，系统的高频特性衰减越快.然而，系统的带宽受到一些内在因素的约束.考虑最为简单的情况，假设系统传递函数G(s)和控制器K(s)都是稳定和严真的，灵敏度函数S(s)满足Bode 灵敏度积分公式

灵敏度积分公式表明:当系统的灵敏度函数的幅值在一段频率范围内小于1 时，必然在另外一段频率范围内的幅值大于1，此即为鲁棒控制领域著名的水床效应［16］，如图6 所示.从设计的角度来说，在期望的频率范围内要使得灵敏度函数幅值频率响应的对数值为负数，则在全频轴上总能找到一段频率范围弥补该负数面积.然而，在实际工程中，灵敏度积分公式式(17)并不完全正确.例如在天线伺服系统中，系统的带宽ωb受到天线结构的第1 个高频谐振频率ω1的约束，文献［17］给出了工程中经过修正的灵敏度积分公式:

修正项δ 是系统带宽ωb的函数［17］，文中采用的某大口径天线的第1 个高频谐振频率为6.4 rad/s.

图6 灵敏度函数的水床效应Fig.6 Water bed effect of sensitivity function

3.2.4 混合灵敏度H_infinity 控制器设计

图7 为天线伺服系统的混合灵敏度H_infinity控制框图.G1表示天线结构和驱动模型的传递函数，G1的输入和输出分别为转矩T 和天线的角速度ω.Kp表示位置控制器，Kv表示速度控制器.Kv设计为比例控制器，Kp设计为混合灵敏度H_infinity 控制器.控制器设计的要求:(1)系统要具有良好的伺服性能;(2)控制信号要在一个合理的范围之内以防止执行器饱和及出现不稳定的控制器;(3)存在高频谐振不确定性和外界低频风扰动时，系统要具有足够的稳定裕量.

图7 混合灵敏度H_infinity 控制框图Fig.7 Block diagram of mixed-sensitivity H_infinity control

灵敏度函数在低频段的特性反映了系统的跟踪性能和干扰抑制性能，而补灵敏度函数在高频段的特性反映了对高频谐振的衰减作用和系统的鲁棒性.灵敏度函数和补灵敏度函数之和S(s)+M(s)=1，无法做到使两者都最小，为了满足系统的性能指标要求，控制工程师要在系统的性能和稳定性之间折中处理.

4 仿真结果

某大口径天线伺服系统的参数取值分别为:Jm=11.37 N·m·s2，k =1，=0.083 s，β =0.25，σp=0.6216 N·s2/m4，c1=0.24，c2=0.22，c3=0.21，c4=0.23.仿真时考虑阵风的风速是稳态风速的10%～20%，阵风扰动的Davenport 谱密度可以用一个低通滤波器近似表示，如图8 所示.

根据实际阵风扰动的频率特征、控制信号的大小、带宽选择需要以及高频谐振的衰减特性等因素综合考虑，选择权重函数W1(s)=100/(170s +1)，W2(s)=5/(s+100)，W3(s)=0.5.

图8 Davenport 谱密度Fig.8 Davenport spectral density

图9 等效开环传递函数频率响应Fig.9 Frequency response of equivalent open-loop transfer function

天线伺服系统的等效开环传递函数频率响应如图9 所示，PID 控制无法克服系统高频谐振的影响，而混合灵敏度H_infinity 控制的作用效果显著.天线伺服系统闭环0.02 度阶跃响应曲线如图10 所示，PID 控制为持续振荡，超调大，且调节时间很长;而混合灵敏度H_infinity 控制的调节时间短，过渡过程平滑，超调量小.在0.4°/s 的斜坡输入信号和外界阵风扰动同时作用下，天线的位置输出如图11 所示，与PID 控制算法相比，混合灵敏度H_infinity 控制算法的稳态伺服误差更小，系统的抗扰动能力更强.仿真研究表明:针对大口径天线伺服系统，混合灵敏度H_infinity 控制比PID 控制效果更好，能够显著改善天线伺服系统的性能指标.

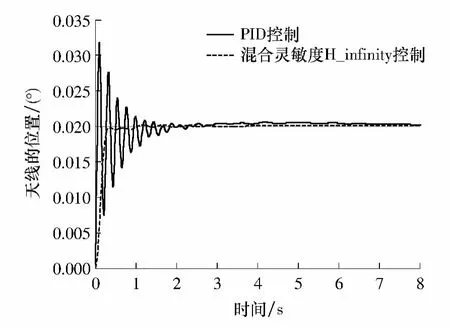
图10 天线0.02°阶跃响应Fig.10 Step response of antenna servo system at 0.02°

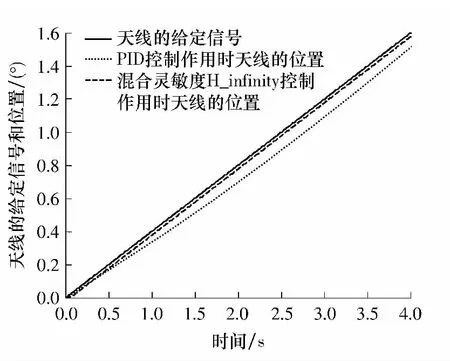
图11 天线系统的伺服误差Fig.11 Servo error of antenna system

5 结语

文中研究了某大口径天线伺服系统的建模和控制算法的设计问题.传统的PID 控制应用于大口径天线系统作用效果欠佳，因此设计了一种基于混合灵敏度的H_infinity 控制算法.仿真结果表明:混合灵敏度H_infinity 控制不仅能够显著地改善天线伺服系统的性能指标，同时具有较强的扰动抑制能力和鲁棒性.

［1］Gawronski W.Control and pointing challenges of large antennas and telescopes［J］.IEEE Transactions on Control Systems Technology，2007，15(2):276-289.

［2］Gawronski W.Modeling and control of antennas and telescopes［M］.New York:Springer，2008.

［3］Liu X，Huang Q，Chen Y.Robust adaptive controller with disturbance observer for vehicular radar servo system［J］.International Journal of Control，Automation，and Systems，2011，9(1):169-175.

［4］Gawronski W，Ahlstrom H G，Bernardo A M.Analysis and performance of the control systems of the NASA 70-meter antennas［J］.ISA Transactions，2004，43(4):597-610.

［5］Cho C H，Lee S H，Kwon T Y，et al.Antenna control system using step tracking algorithm with H∞controller［J］.International Journal of Control，Automation，and Systems，2003，1(1):83-92.

［6］Gawronski W.Antenna control systems:from PI to H∞［J］.IEEE Antennas and Propagation Magazine，2001，43(1):52-60.

［7］朱新颖，张洪波，孔德庆.40m 天线预测控制算法的研究［J］.天文研究与技术，2007，4(2):176-180.Zhu Xin-ying，Zhang Hong-bo，Kong De-qing.Predictive control algorithms for the 40m antenna［J］.Astronomical Research ＆ Technology，2007，4(2):176-180.

［8］王帅，李洪文，孟浩然，等.光电望远镜伺服系统速度环的自抗扰控制［J］.光学精密工程，2011，19(10):2442-2449.Wang Shuai，Li Hong-wen，Meng Hao-ran，et al.Active disturbance rejection controller for speed-loop in telescope servo system ［J］.Optics and Precision Engineering，2011，19(10):2442-2449.

［9］Gawronski W，Racho C S，Mellstrom J A.Application of the LQG and feedforward controllers to the deep space network antennas［J］.IEEE Transactions on Control Systems Technology，1995，3(4):417-421.

［10］张潮海，周其节.位置最优伺服系统的补偿控制［J］.现代雷达，1994，16(2):94-99.Zhang Chao-hai，Zhou Qi-jie.Compensated control for the optimal position servo system ［J］.Modern Radar，1994，16(2):94-99.

［11］Gawronski W，Mellstrom J A，Bienkiewicz B.Antenna mean wind torques:a comparison of field and windtunnel data［J］.IEEE Antennas and Propagation Magazine，2005，47(5):55-59.

［12］Gawronski W.Modeling wind-gust disturbances for the analysis of antenna pointing accuracy［J］.IEEE Antennas and Propagation Magazine，2004，46(1):50-58.

［13］He G L，Li G M，Liu M，et al.The analysis of wind gust disturbances on the cassegrain antenna pointing accuracy［C］∥2009 International Workshop on Intelligent Systems and Applications.Wuhan:IEEE，2009:1-4.

［14］Medrano-Cerda G A，Lett R D，Rees P.H-infinity motion control system for a 2 m telescope ［C］∥Survey and Other Telescope Technologies and Discoveries.Waikoloa:SPIE，2002:88-97.

［15］Skogestad S，Postlethwaite I.Multivariable feedback contorl analysis and design［M］.Chichester:John Wiley ＆Sons，Ltd.，2006.

［16］Zhou K M，Dolye J C.Essentials of robust control［M］.New Jersey:Prentice Hall，1997.

［17］Erm T，Hurak Z，Bauvir B.Time to go H_infinity［C］∥Advanced Software，Control，and Communication Systems for Astronomy.Glasgow:SPIE，2004:68-78.