无人直升机的自适应动态面轨迹跟踪控制*

贺跃帮 裴海龙 叶祥 张谦

(华南理工大学 自主系统与网络控制教育部重点实验室，广东 广州 510640)

无人直升机具有悬停、垂直起降、机动灵活、体积小、成本低等优点，在监视、航拍、救灾、电力寻线等众多领域引起了人们的广泛关注.然而，无人直升机本身是一个非线性、强耦合、不稳定的欠驱动系统.因此，飞行控制器设计成为了一个很具有挑战性的研究领域［1-2］.

近20 年来，许多控制方法已成功地应用于无人直升机的自主控制.由于通过线性辨识技术很容易获得悬停处的线性化模型［3］，因此线性控制器如PID［4］、线性二次型调节器/线性二次型高斯调节器(LQR/LQG)［5］、H∞［6］、μ 综合［7］等得到了广泛的应用.然而，线性控制器只能保证悬停点附近的性能，当飞行速度增加或机动飞行时，系统性能急剧下降甚至不稳定.之后，很多研究人员开始尝试将非线性控制方法应用到直升机飞行控制中，如增益调度［8］、模型预测控制(MPC)［9］、神经网络［10］、反步法［11-13］等.其中反步法由于设计过程系统化，系统稳定性和鲁棒性也能得到保障，在最近几年成为了研究的热点.文献［11］针对简化的无人直升机系统，采用常规反步法控制器设计，获得了一定的鲁棒性能.文献［12］在考虑直升机负载变化的情况下，采用自适应积分反步法，获得了质量大范围变化下的稳定性能.文献［13］针对无人直升机阶数高、精确建模困难、外部干扰大等缺点，提出一种鲁棒积分滤波反步法，解决了常规反步法计算量大、抗干扰能力不足、轨迹跟踪效果差等问题.然而，常规反步法在递推过程中需要不断地对中间虚拟控制信号求导，对于无人直升机这种模型阶数比较高的系统，其计算过程将变得非常繁琐，虽然文献［13］提出采用滤波器求导的方法可以简化计算量，但是其在每步的设计过程中都要补偿前步留下的控制误差，因而造成各步之间相互耦合.当控制器参数较小时，这种耦合就起主导作用，使得闭环系统响应对控制参数的调整不敏感.因此，反步法在无人直升机这种位置动态缓慢的系统中应用时也无法满足实际工程师对现场调参的需要.

针对反步法存在的微分”爆炸”和控制参数对闭环输出响应不敏感的问题，Swaroop 等［14］提出了动态面控制，克服了反步法控制技术的缺点.在此基础上，众多研究人员根据各种需求研究了动态面技术与自适应技术［15］、鲁棒技术［16］、智能技术［17］等各种先进控制技术相结合的组合控制方法，并广泛应用于机器人和机械臂控制中［18-19］.

动态面控制技术解决了反步法设计过程中存在的微分“爆炸”问题，而且设计过程中每一步都无需补偿前步遗留的控制误差，因而不存在闭环系统响应对控制参数调整不敏感的问题.因此，文中设计了一种基于自适应动态面法的无人直升机轨迹跟踪控制方法.该方法简化了控制器的设计过程，控制器参数的变化也显著影响位置动态响应，可极大地方便实际应用工程师现场调参，同时通过自适应律在线估计直升机重量，保证了闭环系统在大质量变化下(有负载变化)的稳定性和轨迹跟踪性能.

1 无人直升机模型

无人直升机受到重力、空气动力和驱动力的作用，可以视为在三维空间内的刚体运动.设P =(x，y，z)T和V=(u，v，w)T分别为直升机质心在惯性坐标系下的位置矢量和速度矢量;ω=(p，q，r)T，为相对于机体坐标系下的角速度矢量;m 为直升机质量;Im∈R3×3，为直升机本身惯性矩阵.根据牛顿欧拉方程，可得无人直升机动态微分方程为

式中:姿态角向量η =(φ，θ，ψ)T，φ、θ、ψ 分别表示滚转角、俯仰角和偏航角;sk(ω)表示斜矩阵，

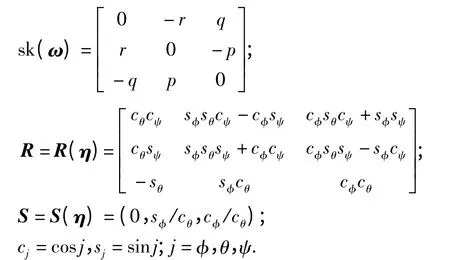
当飞行速度不大时，所受合力F 和合力矩Γ 可简化描述如下:

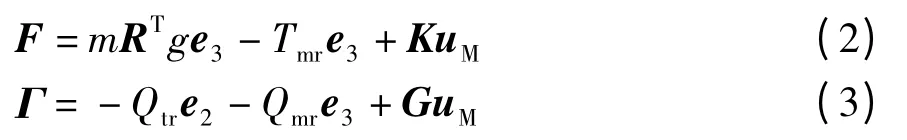
式中:g 表示重力加速度;Qmr和Qtr分别表示主旋翼和尾旋翼受到的反扭力矩;Tmr表示直升机升力控制量;uM=(Lmr，Mmr，Nmr)T∈R3，表示机体坐标系下3 个方向的力矩控制量;e3=(0，0，1)T;K、G 为系数矩阵，可表示为

式中，hmr表示浆毂中心到质心垂向距离，ltr表示尾旋翼中心到质心距离，kβ表示主旋翼弹性系数.

2 基于自适应动态面的轨迹跟踪控制

首先给出系统设计需满足的假设条件.

假设1 期望轨迹Pd(t)充分光滑且Pd(t)∈Ωd，其中

假设2 期望航向角ψd充分光滑且ψd∈Ωψ，其中

对无人直升机飞行参考轨迹来说，以上两条假设都成立，且常数ε0、ε1一般不大.

控制器的设计包括4 步.

步骤1 定义轨迹跟踪误差面矢量

求导并代入式(1)可得

其中k1为控制器参数，且k1＞0.

式中:1为滤波器的时间常数

步骤2 定义第2 个误差面矢量s2=V-Vd，将s2对时间求导并代入式(1)可得

式中:2、d为滤波器的时间常数，均大于0;Xd(0)=

选择升力控制量Tmr为

姿态角虚拟控制量ηd=(φd，θd，ψd)T，满足

其中E=diag(1，1，0).

对直升机而言，Yd是小量，当仅考虑(φd，θd)∈时，对给定的偏航角ψd，式(13)存在唯一解φd、θd.由于式(13)是一个二元非线性方程，因此φd、θd的求解非常复杂.为减小计算量，同时考虑当R-R(ηd) 0 时，有η-ηd0，文中将R(ηd)作为虚拟控制量.

选择自适应律如下:

式中:γ1为自适应控制参数，γ1＞0;mmax表示直升机满载质量;mmin表示直升机空载质量.

步骤3 定义第3 个误差面矢量

s3=E(R-R(ηd))TXd+e3(ψ- ψd)，并将s3对时间求导且代入式(1)、(13)可得

式中，N1=Esk(RTXd)+e3S，N2=E(RTd+d)-e3d.

定义

式中，ξ1、ξ2表示滤波误差.则经过一系列复杂计算，N1可描述成如下形式

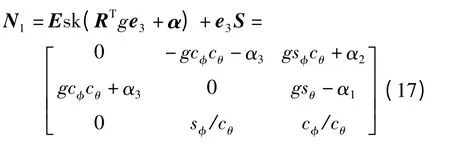
求N1的行列式可得

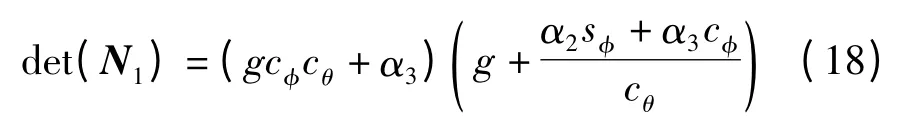
比较式(18)和式(16)可得det(N1)≠0(即N1非奇异)的一个充分条件是

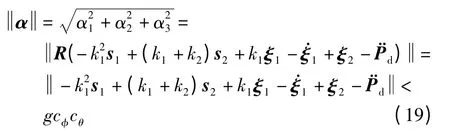
其中k3、3分别为控制器参数和滤波器时间常数，均大于0，ωd(0)=(0).

步骤4 定义第4 个误差面矢量s4=ω- ωd，将s4对时间求导并代入式(1)可得

选择控制输入uM为

其中k4为控制参数，k4＞0.

3 稳定性分析

定理1 在假设1 和假设2 成立的条件下，对给定的ki＞0(i=1，2，3，4)，γ1＞0，存在足够大的 d和i(i=1，2，3)使得无人直升机系统(1)在控制律(12)、(22)以及自适应律(14)的控制下，轨迹跟踪误差半全局一致最终有界，且适当选取设计参数，跟踪误差可收敛到原点的一个小邻域内.

证明 定义滤波误差

对ξ1、ξd、ξ2以及ξ3求导并整理可得

控制器中4 个误差面的导数可整理为

取李雅普诺夫函数

式中，i(i=1，2，3，4)为正数.

对V 求导并代入式(24)、(25)，并整理可得

将自适应律(14)代入上式，同时根据RTR =diag(1，1，1)，，以及Young’s 不等式，上式可整理成

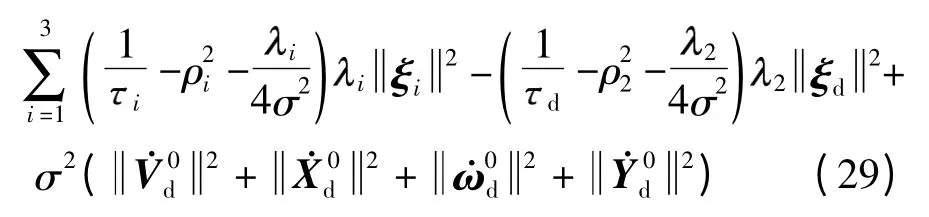
式中:ρi(i=1，2，3)，σ 为正数.

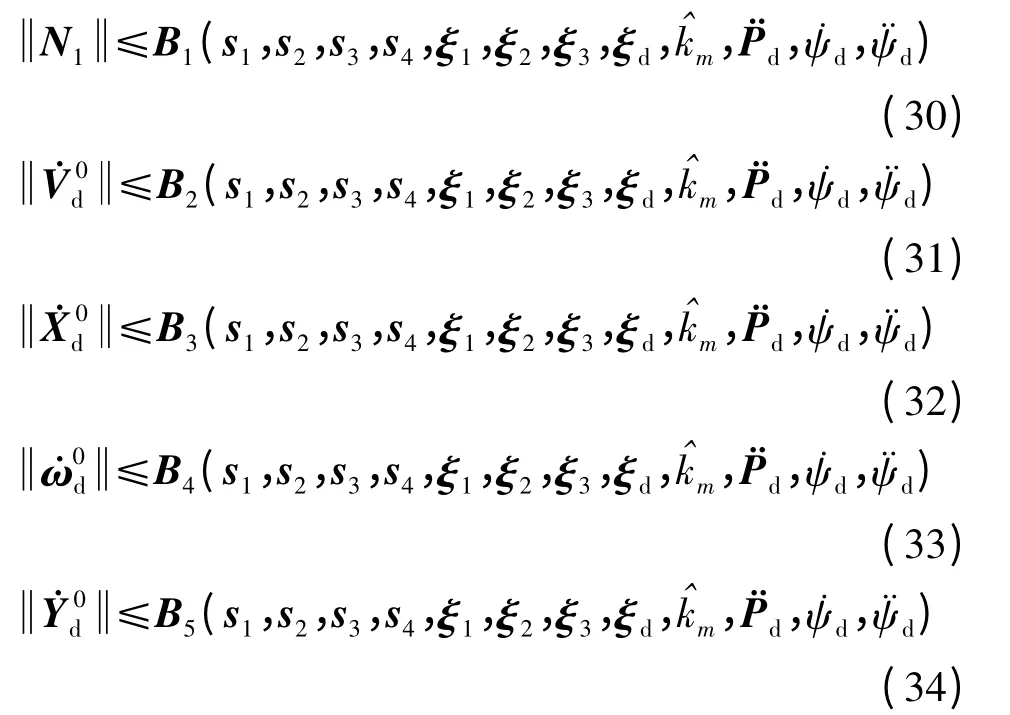
式中，Bi(i=1，2，…，5)为连续函数.

定义紧集

其中ε2是可确定的常数.

注意到Ω×Ωd×Ωψ也是紧集，其中Ωd、Ωψ是假设1 和2 中的紧集，^km有界(见自适应律(14))，因此，Bi在集合Ω × Ωd× Ωψ内存在最大值，记为Mi.同时取

式中，κ0为正数.则有

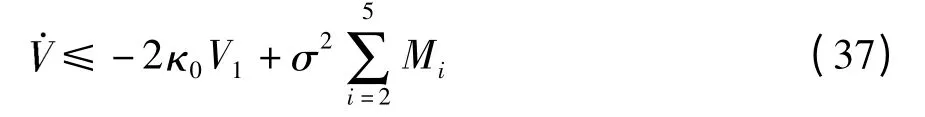
注意到式(36)中对任意的控制器参数ki＞0(i=1，2，3，4)，都存在合适的参数i(i =1，2，3，4)、ρi(i =1，2，3)以及足够大的参数i(i =1，2，3)和 d 使得κ0＞0，σ 任意小.

式(38)两边同乘e2κ0t，并从0 到t 积分得

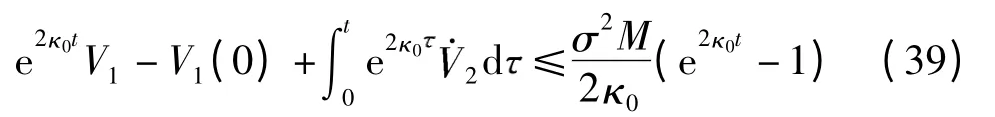
根据分部积分法有

将式(40)代入式(39)，并两边同除e2κ0t，得

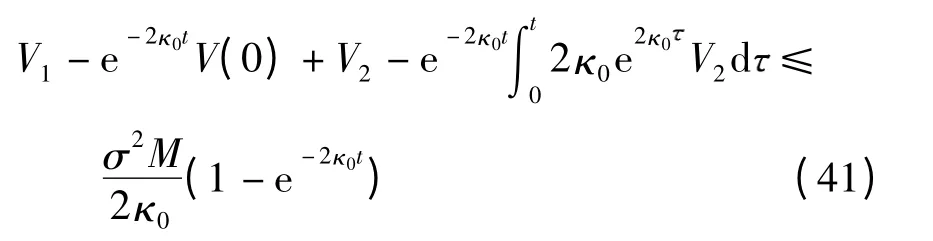
4 仿真结果

通过两个仿真实验验证文中所提方法的有效性.第1 个仿真实验检验闭环系统的悬停能力以及闭环系统响应是否对控制参数敏感.第2 个实验检验闭环系统在受到干扰和质量变化下的轨迹跟踪能力.无人直升机模型相关参数见表1，自适应动态面控制器参数见表2.

表1 无人直升机参数Table 1 Parameters of unmanned helicopter

表2 控制器参数Table 2 Controller parameters

4.1 悬停仿真

假设无人直升机初始位置Pd= (-1，-1，1)T(单位:m)，初始偏航角ψd=-90°，控制目标是要求无人直升机悬停于原点.控制器参数选择表2 中方案，并以同样的参数设计反步法控制器.仿真结果如图1、2 所示.

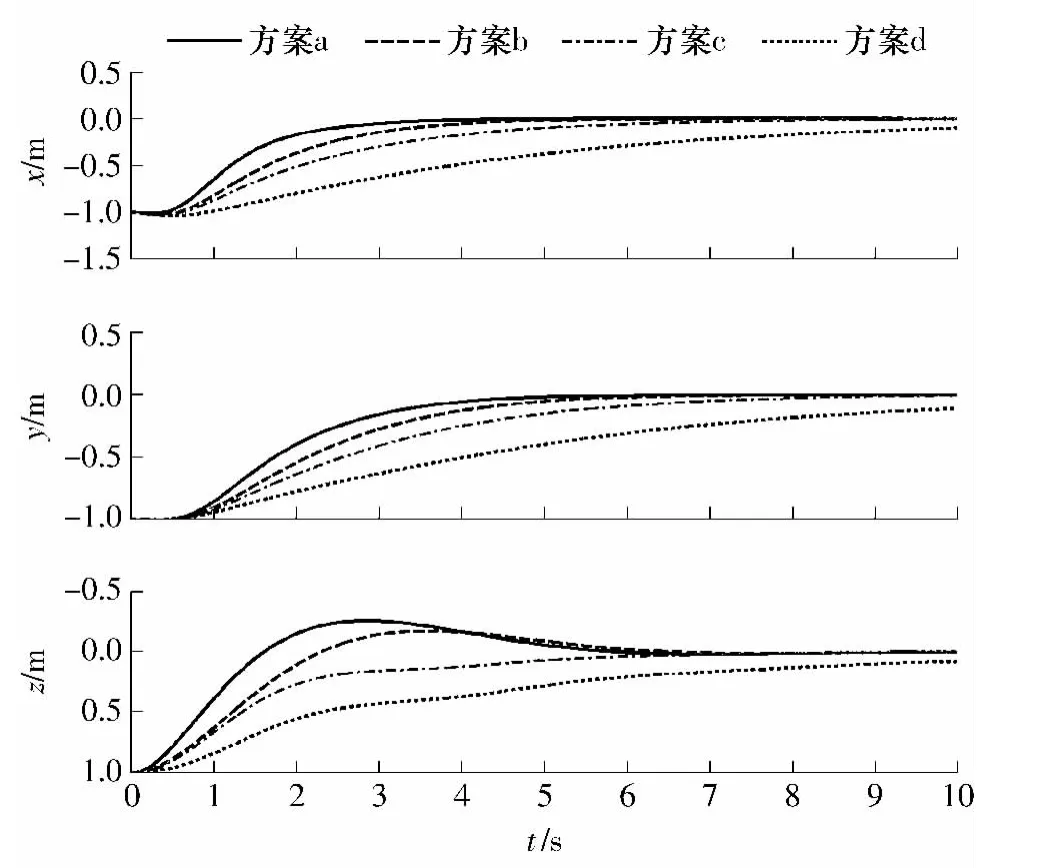
图1 应用动态面控制方法的无人直升机位置响应Fig.1 Position responses of unmanned helicopter by use of dynamic surface control approach

图2 应用反步法的无人直升机位置响应Fig.2 Position responses of unmanned helicopter by use of backstepping control method

从图1、2 可以看出，两种方法都能稳定无人直升机系统.但是反步法由于在设计过程中每步都要补偿前步留下的控制误差，因此造成各步之间相互耦合;当控制器参数较小时，这种耦合就起主导作用，使得闭环系统响应对控制参数的调整不敏感.相反，采用文中提出的动态面控制方法，闭环系统动态响应明显受控制器参数调整的影响.这极大地方便了实际应用中工程师的现场调试.

4.2 轨迹跟踪仿真

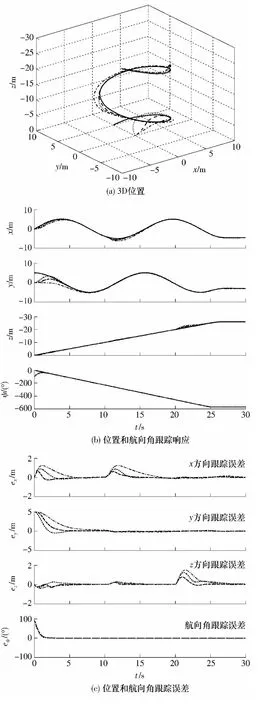
定义如下参考跟踪轨迹:Pd= (5sin(0.4t)，5cos(0.4t)，-t)T、ψd=-0.4t，其中t 表示时间.自适应动态面控制器参数选择表2 中方案a 和c.直升机初始位置Pd(0)=(0，0，0)T，初始偏航角ψ(0)=-90°.仿真过程中，假设在t =10 s 时，直升机沿机体坐标x 和y 方向分别受到30 N 的外界扰动力作用，持续时间为1 s.同时在t=20 s 时，直升机卸掉负载，质量由m=19.2 kg 变为m-mp=9.6 kg.仿真结果见图3.

由图3(a)-(d)可以看出，通过合适地选择参数，基于自适应动态面法控制的无人直升机闭环系统，在避免对虚拟控制量繁琐的解析求导过程的情况下，轨迹跟踪结果接近基于自适应反步法设计的控制器的性能指标.从图3(e)、(f)可以看出，通过合适地选择参数，基于自适应动态面控制的无人直升机闭环系统，其俯仰角和滚转角动态响应以及旋翼力和力矩控制量动态要明显好于自适应反步法.当x 和y 方向受到持续1 s 的大扰动作用时，跟踪轨迹都出现一定误差，但随后都收敛到期望轨迹附近.当直升机卸掉负载后，机体坐标z 方向出现一定跟踪误差，但随着质量自适应估计结束，误差也都收敛到期望轨迹附近. 虽然自适应动态面方案 c 在抗干扰和大质量变化下轨迹跟踪性能要弱于方案 a，但姿态角响应要好于方案 a. 因此，通过合适地选择参数，可以在姿态角响应需求以及轨迹跟踪和抗干扰性能需求之间获得一个合理的折中，而采用自适应反步法无法满足实际无人直升机控制时对姿态角响应不宜过大的要求. 更有利的是，自适应动态面控制器方便工程师现场调试参数，使其能够更直观地获得满意的控制效果

5 结语

针对常规反步法在无人直升机这种模型阶数比较高、位置动态缓慢、负载变化大的系统中应用的缺陷，文中设计了一种基于自适应动态面法的控制方法.该方法通过一阶滤波器对虚拟控制信号求导，显著简化了控制器的设计过程，而且相比反步法，控制器参数的变化更能影响位置动态响应，从而方便实际应用工程师现场调参，同时通过质量自适应估计，保证了闭环系统在大质量变化下的稳定性和轨迹跟踪性能.基于李雅普诺夫稳定性理论的稳定性分析和仿真结果都证实了该方法的有效性和可行性，为下一步将自适应动态面法应用到实际飞行实验中提供了理论基础.

［1］Gavrilets V.Autonomous aerobatic maneuvering of miniature helicopters［D］.Boston:Department of Aeronautics and Astronautics，Massachusetts Institute of Technology，2003:31-54.

［2］Cai G，Chen B M，Lee T H.Unmanned rotorcraft systems［M］.Heidelberg:Springer，2011:97-128.

［3］Tischler M B.Aircraft and rotorcraft system identification［M］.Virginia:American Institute of Aeronautics and Astronautics，2003:321-430.

［4］Kim H J，Shim D H.A flight control system for aerial robots:algorithms and experiments［J］.Control Engineering Practice，2003，11(2):1389-1400.

［5］Gribble J J.Linear quadratic gaussian/loop transfer recovery design for a helicopter in low-speed flight［J］.Journal of Guidance，Control，and Dynamics，1993，16(4):754-761.

［6］Cai G W，Chen B M，Dong X，et al.Design and implementation of a robust and nonlinear flight control system for an unmanned helicopter ［J］.Mechatronics，2011，21(5):803-820.

［7］Sun X D，Clarke T.Application of hybrid μ/H∞control to modern helicopters［C］∥Proceedings of the International Conference on Control'94.Part2.Stevenage:IEE，1994:1532-1537.

［8］Oosterom M，Babuška R.Design of a gain-scheduling mechanism for flight control laws by fuzzy clustering［J］.Control Engineering Practice，2006，14(7):769-781.

［9］Liu C，Chen W H，John A.Tracking control of small-scale helicopters using explicit nonlinear MPC augmented with disturbance observers［J］.Control Engineering Practice，2012，20(3):258-268.

［10］Chen M，Ge S S，Ren B.Robust attitude control of helicopters with actuator dynamics using neural networks［J］.IET Control Theory and Applications，2010，4(12):2837-2854.

［11］Mahony R，Hamel T.Robust trajectory tracking for a scale model autonomous helicopter ［J］.International Journal of Robust and Nonlinear Control，2004，14(12):1035-1059.

［12］Lee C T，Tsai C C.Adaptive backstepping integral control of a small-scale helicopter for airdrop missions［J］.Asian Journal of Control，2010，12(4):531-541.

［13］贺跃帮，裴海龙，赵运基，等.无人直升机鲁棒积分滤波反步法飞行控制设计［J］.华南理工大学学报:自然科学版，2013，41(2):30-36.He Yue-bang，Pei Hai-long，Zhao Yun-ji，et al.Flight control design of unmanned helicopter based on robust integral filtering backstepping［J］.Journal of South China University:Natural Science Edition，2013，41(2):30-36.

［14］Swaroop D，Hedrick J K，Yip P P，et al.Dynamic surface control for a class of nonlinear systems［J］.IEEE Transactions on Automatic Control，2000，45 (10):1893-1899.

［15］王允建，刘贺平，王玲.自寻优自适应动态面控制［J］.控制与决策，2010，25(6):939-942，957.Wang Yun-jian，Liu He-ping，Wang Ling.Self-optimize adaptive dynamic surface control［J］.Control and Decision，2010，25(6):939-942，957.

［16］Song B.Robust stabilization of decentralized dynamic surface control for a class of interconnected nonlinear systems［J］.International Journal of Control，Automation，and Systems，2007，5(2):138-146.

［17］Zhou L，Fei S，Jiang C.Adaptive integral dynamic surface control based on fully tuned radial basis function neural network［J］.Journal of Systems Engineering and Electronics，2010，21(6):1072-1078.

［18］张天平，华森.基于观测器的机器人动态面控制［J］.控制工程，2009，16(5):630-633.Zhang Tian-ping，Hua Sen.Dynamic surface control of robot manipulators based on states observer［J］.Control Engineering of China，2009，16(5):630-633.

［19］顾义坤，倪风雷，刘宏.基于RENN 的柔性关节机械臂自适应动态面控制［J］.控制与决策，2011，26(12):1783-1790.Gu Yi-kun，Ni Feng-lei，Liu Hong.Flexible-joint manipulator adaptive control based on recurrent Elman neural networks and dynamic surface approach［J］.Control and Decision，2011，26(12):1783-1790.