一种免疫控制器在飞轮BLDCM中的应用*

徐立芳 莫宏伟

(1.哈尔滨工程大学 工程训练中心，黑龙江 哈尔滨 150001;2.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

飞轮储能系统是一种利用高速旋转的惯性飞轮将电能转换为动能储存的装置，可应用于电网调频［1］、电能质量治理［2］、车辆再生制动［3］以及高功率脉冲电源［4］等领域.不平衡转动力矩作用是飞轮转速改变的根本原因.当转动力矩方向与飞轮转动方向一致时，飞轮受到正向不平衡转矩作用加速，电能转化为动能储存起来;相反，飞轮减速，动能转化为电能.目前，飞轮储能系统通常采用感应电机、开关磁阻电机或无刷直流/交流电机技术［5］，而对于转速达到20000 r/min 左右的飞轮储能系统，其电机选择以无刷直流电机(BLDCM)技术居多，例如:美国Indigo 能源公司的飞轮储能系统就采用了三相高速永磁无刷直流电机，其反电势波形为方波，能量转换效率高达95%［6］.

一方面，飞轮储能系统内置高速永磁无刷直流电机运行时，在方波驱动方式下其输出的转矩波动非常大，会导致飞轮储能系统运行稳定性变差，振动增大.另一方面，高速永磁无刷直流电机的快速启动是无刷直流电动机控制的难点之一，传统的BLDCM调速系统常采用PID 控制，系统输出误差较大.

文献［7］研究了应用于飞轮储能永磁无刷直流电机的PWM 变换器.文献［8］通过电流超前控制减小永磁无刷直流电机转矩脉动.文献［9］解决了飞轮无刷直流电机的PWM 调节过程中电动机电流上升过慢的问题，设计了电动机驱动系统，电机转数达到10500 r/min.文献［10］将模糊控制与滑模控制相结合，有效减小了飞轮控制系统抖振.文献［11］将免疫控制器用于飞轮系统速度环电流控制，能够获得优于PID 控制器的控制效果.文献［12］提出了飞轮储能型二次调节流量耦联系统，该系统可把原来系统负载下降时转化为热能散失掉的势能存储为飞轮机械动能.

鉴于飞轮储能系统是一个多变量、非线性、强耦合的控制对象，惯性飞轮转矩负载变化产生的扰动、模型误差对飞轮电机高速运行或调速运行的影响都将会导致飞轮无刷直流电机PID 控制系统性能变差.飞轮电机系统仅靠传统的参数测量、辨识、补偿控制方法很难取得满意的稳定性和动态特性.Varela 免疫网络模型是Varela 等［13］在1990 年提出的，付冬梅等［14］对其进行了改进，并用于大滞后大惯性对象控制.研究表明，该网络模型具有较好的抗纯滞后及参数自适应能力.

文中利用Varela 免疫网络模型方法，将免疫控制器用于飞轮无刷直流电机的转速和力矩控制，与PID控制器相比，免疫控制器能够使飞轮无刷直流电机保持16000 r/min 的高速稳定运行，有效降低电机转矩脉动幅值，使控制系统输出电流信号波形畸变小.

1 飞轮无刷直流电机控制系统

飞轮无刷直流电机控制系统主要由逆变器、无刷直流电机、检测电路、控制电路、驱动电路构成，如图1 所示.图中，D1至D6为晶闸管，V1至V6为晶闸管端电压，A、B、C 为电机的三相，PM 为永磁.

1.1 飞轮无刷直流电机模型

为了简化模型计算，对飞轮无刷直流电机数学模型［15］做如下假设:定子三相完全对称;钕铁硼永久磁铁的磁导率与空气的磁导率相同，每相绕组的自感为一常数;忽略齿槽效应和磁路饱和，不计涡流和磁滞损耗、集肤效应和温度对参数的影响;不考虑电枢反应，气隙磁场分布近似为矩形波，平顶宽度为120°电角度;转子上没有阻尼绕组，永磁体不起阻尼作用.那么，飞轮无刷直流电机定子三相绕组的电压平衡方程为

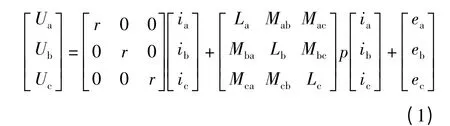
式中:Ua、Ub、Uc为定子三相绕组的相电压;ia、ib、ic为定子三相绕组的相电流;ea、eb、ec为定子三相绕组的相电动势;La、Lb、Lc为定子三相绕组的自感;Mab、Mac、Mba、Mbc、Mca、Mcb为定子每两相绕组间的互感;，为微分算子;由于电机三相绕组完全对称，所以La=Lb=Lc，Mab=Mac=Mba=Mbc=Mca=Mcb;令L=La，M=Mab，则定子电压方程简化为

当电机三相绕组星型连接没有中线时，根据基尔霍夫定理可得

并且满足

将式(3)和(4)代入式(2)得

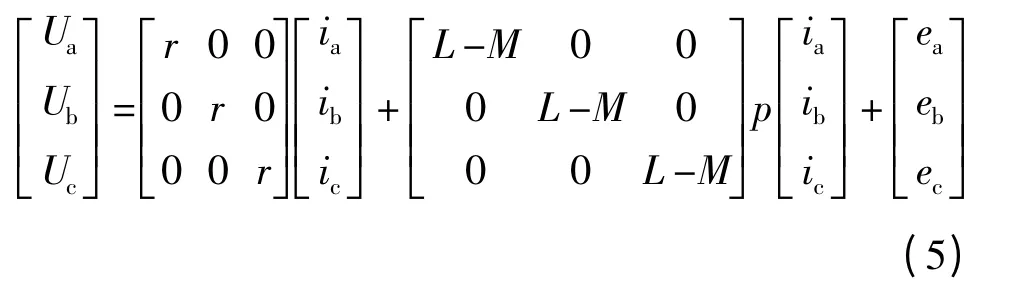
飞轮直流无刷电机的电磁转矩为

式中，ω 为转子角速度.

飞轮直流无刷电机的机械方程为

式中:TL为负载转矩;B 为粘滞摩擦系数;J 为飞轮转动惯量.

文中采用的飞轮电机基本设计指标，来源于哈尔滨工程大学飞轮储能研究所设计的飞轮储能样机内置永磁无刷直流电机，额定转速为20 000 r/min，极对数为2，额定功率为8 kW，额定电压为610 V，惯性距为0.002051 kg·m2，定子每相绕组电阻为0.7758 Ω，电机相电感为0.0014 H.

1.2 逆变器与电机开关换相控制

飞轮储能系统内置BLDCM 为星形三相六状态电机结构，见图1.电枢绕组安放于定子铁心中，永磁体固定在转子上，利用转子位置传感器检测永磁磁极的位置，据此确定定子绕组的导通状态，使电机产生稳定持续的电磁转矩.图1 中V1至V6为功率开关管，通过控制电路控制其开关次序.每隔 /3 产生一个脉冲宽度为2 /3 的方波脉冲.该方波脉冲与脉宽调制器产生的脉宽信号经过与门运算产生6 路驱动信号作为逆变器的驱动信号输入，从而控制飞轮无刷直流电机绕组的开关换相.由于采用了PWM控制，在功率开关管的120°导通区间内电流有脉动，会使电机电压和转矩也产生脉动.

2 免疫控制器的建立

Varela 免疫网络模型［11］可由如下差分方程表示:

式中:k1-k6为免疫网络的调节系数;fi和bi分别为第i 种克隆抗体和B 细胞的浓度.式(9)中的3 项分别为抗体间相互作用导致的抗体死亡率、抗体的自然死亡率和B 细胞生成的新抗体;式(10)中的3 项分别为B 细胞的自然死亡率、B 细胞的繁殖率以及由骨髓生成的B 细胞.M()和P()分别为B 细胞的成熟函数和繁殖函数，σi表示第i 种克隆对网络的敏感度:

式中，p1和p2为自然底数e 的调节系数;mij为第i种克隆和第j 种克隆亲和力作用的布尔值，mij=1表示有亲和力作用，mij=0 表示没有.h 是Bi细胞和Ti抗体的种类，i =1，2，…，h.成熟函数和繁殖函数是类似“钟”形函数.

式(9)和(10)在一定程度上反映了人工免疫过程中B 细胞和抗体T 之间相互作用的动态过程，但是该控制器中没有反映抗原的作用.

构建免疫控制器的基本框架是免疫反馈规则，将控制系统中的误差等效为免疫系统中的抗原.而在上述Varela 免疫网络模型的动力学方程中，并没有涉及到入侵抗原.因此为使该网络模型能够用于控制领域，付冬梅等［11］对其进行了改进，引入抗原的作用.

抗原进入机体内会受到两种不同的反应，在Varela 免疫模型中引入抗原作用:一是抗原的自我复制和繁殖，用fi和ai分别表示第i 种抗体和抗原，k7表示自我复制和繁殖过程的调节系数;二是受到抗体的清除.假设抗原的清除主要靠抗体与抗原相遇并结合来实现，用抗体数量和抗原数量的乘积fiai来表示，k8为抗体清除过程的调节系数，则可得

联立式(9)、(10)、(14)便可得到该控制模型的动力学方程.

由于该模型中的控制量与实际控制系统的控制量存在出入，根据实际情况进行如下调整与简化:

(1)进入机体的抗原变化率由抗原的自我复制和抗体对抗原的杀伤率两部分组成，而在实际控制系统中，偏差不存在自我复制现象，因此去掉式(9)中的第1 项;

(2)抗原进入机体后，会刺激B 细胞增值，用偏差e(t)代替抗原ai，将式(10)增加一项k9e(t)得

式中，k9为偏差e(t)自我复制和繁殖的调节系数.

(3)令M(σi)的自变量为bi，P(σi)的自变量为并用偏差e(t)代替抗原ai，用控制量u(t)代替B 细胞浓度bi;

因为该系统为单入单出控制系统，经过简单迭代［16］，得到经调整后的Varela 免疫控制器模型

式中:k10为抗体调节系数，k11为抗体清除过程的调节系数;u(t)表示控制量;f0表示无抗原侵入时存在的少量记忆抗体，f(0)=f0.将成熟函数M(σ)和繁殖函数P(σ)均取如下非线性函数:

式中:σ 为函数M(σ)和P(σ)的自变量;Km是常数，Km＞0;p1和p2也是常数，p2＜p1＜0.

M(σ)和P(σ)在Km取不同参数的情况下具有“钟”型结构形式，这是为了适应实际飞轮BLDCM控制系统中各控制变量有正有负的实际情况.

3 仿真实验与分析

3.1 飞轮BLDCM 的转速控制

根据式(16)描述的免疫控制器模型，在Matlab/Simulink7.0 中建立免疫控制器对飞轮BLDCM 转速进行控制的Simulink 模型，见图2;BLDCM 拖动3.5N·m的飞轮负载高速转动，进行飞轮储能运行.

文中采用的免疫控制器控制参数选取为多次实验中获得的最优数值:k3=0.001，k4=15.5，k5=0.000001，k10=600，k11=57，p1=-0.1，p2=-0.10001，Km=5.仿真实验结果见图3-5.

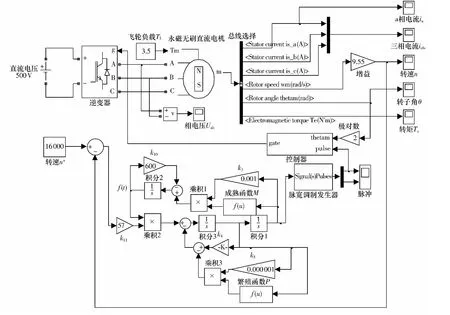
图2 免疫控制电机转速的Simulink 框图Fig.2 Simulink framework of motor speed controlled by immune controller

由图3 可见，PID 控制系统与免疫控制系统输出均无超调;与PID 控制系统相比，免疫控制器控制下的飞轮电机转速响应误差相对较小，稳态调节时间较短，可控制在1 min 以内;当电机转速超过14000 r/min后，免疫控制系统中的电机加速明显.

由图4 可见，与PID 控制器相比，免疫控制器控制下的飞轮电机输出电磁转矩脉动较大，飞轮电机启动初期，最大电磁转矩输出相对较小.

图3 BLDCM 的转速控制响应Fig.3 Speed control response of BLDCM

图4 BLDCM 的电磁转矩输出Fig.4 Electric magnetic torque output of BLDCM

由图5 可见，与PID 控制器相比，免疫控制器控制下飞轮电机输出电流波形谐波较强，波形存在一定的畸变，但飞轮电机电流输出数值较小.

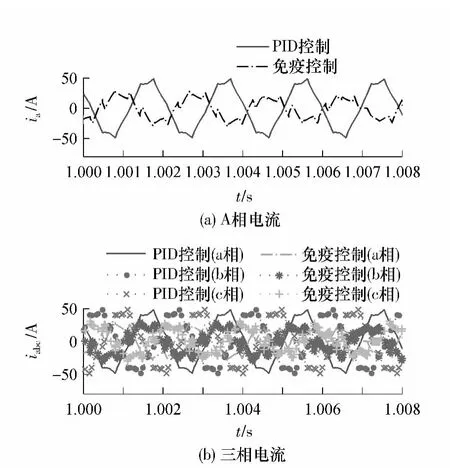
图5 BLDCM 的电流输出Fig.5 Current output of BLDCM

由上述实验分析可知，免疫控制器用于飞轮直流无刷电机转速控制，能够获得优于PID 控制器的控制系统动态响应，但是飞轮电机电磁转矩输出脉动较大，因此考虑利用免疫控制器建立一个转矩闭环控制系统，用于解决飞轮电机电磁转矩输出控制效果不良的问题.

3.2 飞轮BLDCM 的转矩控制

根据式(16)描述的免疫控制器模型，在Matlab/Simulink7.0 中建立免疫控制器对飞轮BLDCM 的转矩内环进行控制，外环采用PID 调节器控制电机转速，BLDCM 拖动3.5 N·m 的飞轮负载高速转动，进行飞轮储能运行，见图6.

同时建立一个转矩、转速双闭环均采用PID 控制器的飞轮电机控制系统进行对比试验，实验中PID 控制器控制参数的设置见表1，为多次实验中获得的最优数值.免疫控制器控制参数设置k11=70，其余控制参数设置与表1 中数值相同.仿真实验结果见图7-9.

图6 免疫控制电机电磁转矩的Simulink 框图Fig.6 Simulink framework of motor electric magnetic torque controlled by immune controller

表1 PID 控制参数设置Table 1 PID control parameter settings

由图7 可见:PID 控制系统与免疫控制系统输出均无超调;免疫控制器控制下的飞轮电机转速控制响应误差相对较小，稳态调节时间较短，可控制在1.5 min 以内.

由图8 可见，免疫控制器控制的飞轮电机电磁力矩输出转矩脉动波动范围可控制在4.0～4.6 N·m;与采用PID 控制器相比，飞轮电机转矩闭环采用免疫控制器可获得良好的转矩脉动抑制效果.

由图9 可知，与PID 控制器相比，免疫控制器控制的飞轮BLDCM 输出电流波形畸变较小，接近理想梯形波，电流输出数值较小.

图7 双闭环系统的BLDCM 转速控制响应Fig.7 BLDCM speed control response of double closed-loop control system

图8 双闭环系统的BLDCM 电磁转矩输出Fig.8 Output of BLDCM electric magnetic torque of double closed-loop control system

图9 双闭环系统的BLDCM 电流输出Fig.9 Output of BLDCM current of double closed-loop control system

4 结论

文中基于Varela 免疫网络模型，将建立的免疫控制器用于飞轮储能系统的直流无刷电机控制.研究结果表明，与传统PID 控制器相比，文中提出的免疫器具备以下优良特性:电机转速控制下的系统动态响应无超调，信号输出稳定;在飞轮储能电机转速-转矩双闭环控制系统中，将免疫控制器用于飞轮BLDCM 转矩控制，飞轮电机输出电磁转矩脉动幅值较小，转矩信号变化稳定，且有一定的周期性;系统输出的电流波形畸变较小，接近理想梯形波;控制参数自适应性好(电机转速和转矩控制实验基本采用了相同的控制参数设置).基于Varela 免疫网络模型的免疫控制器作为一种新型控制器用于飞轮储能系统内置BLDCM 控制具有一定的实际应用价值.

［1］Ray P K，Mohanty S R，Kishor N.Frequency regulation of hybrid renewable energy system for large band wind speed variation［C］∥Proceedings of 2009 Third International Conference on Power Systems Technoloy.Kharagpur:IEEE Press，2009:1-6.

［2］Samineni S，Johnson B K，Hess H L，et al.Modeling and analysis of a flywheel energy storage system for voltage sag correction［J］.IEEE Transactions on Industry Applications，2006，42(1):42-52.

［3］Brown D R，Chvala W D.Flywheel energy storage:an alternative to batteries for UPS systems［J］.Energy Engineering，2005，102(5):7-26.

［4］Swett D W，Blanche J G Ⅳ.Flywheel charging module for energy storage used in electromagnetic aircraft launch sys-tem［J］.IEEE Transactions on Magnetics，2005，41(1):525-528.

［5］Zmood R B，Qin L J，Kirk J A，et al.A Magnetic bearing system design methodology and its application to a 50 Wh open core composite flywheel ［C］∥Proceedings of the 32nd Intersociety (Energy Conversion Engineering Conference，1997，IECEC-97).Honolulu:American Institute of Chemical Engineers，1997:2306-2311.

［6］李俄收，王远，吴文民.超高速飞轮储能技术及应用研究［J］.微特电机，2010(6):65-68.Li E-shou，Wang Yuan，Wu Wen-min.Application and energy storage technology for ultra-h igh speed flywheels［J］.Small ＆ Special Electrical Machines，2010(6):65-68.

［7］Oliveira J G，Larsson A，Bernhoff H.Controlling a permanent-magnet motor using PWM converter in flywheel energy storage systems ［C］∥Proceedings of 34th Annual Conference of the IEEE Industrial Electronics Society(IECON 2008).Orlando:IEEE Press，2008:3364-3369.

［8］Park S I，Kim T S，Ahn S C，et al.An improved current control method for torque improvement of high-speed BLDC motor［C］∥Proceedings of the 18th IEEE Annual Applied Power Electronics Conference and Exposition.Miami Beach:IEEE，2003:294-299.

［9］李悦溪，王萌，祝长生.飞轮储能系统用无刷直流电机驱动系统的设计［J］.机电工程，2010，27(10):68-73.Li Yue-xi，Wang Meng，Zhu Chang-sheng.Design of brushless DC motor driver system for flywheel energy storage system［J］.Journal of Mechanical ＆ Electrical Engineering，2010，27(10):68-73.

［10］Song H L，Yu Y，Yang M，et al.A novel SMC-fuzzy speed controller for permanent magnet brushless DC motor［C］∥IEEE APEC'03.Miami Beach:IEEE Press，2003:281-285.

［11］Xu L F，Jiang S D.Research of dynamics of DC speed regulator of flywheel double closed loop based on immune principle［C］∥Proceedings of 2011 IEEE International Conference on Computer Science and Automation Engineering.Shanghai:IEEE Press，2011:259-263.

［12］刘海昌，姜继海.飞轮储能型二次调节流量耦联系统［J］.华南理工大学学报:自然科学版，2009，37(4):75-79.Liu Hai-chang，Jiang Ji-hai.Flow-coupled secondary regulation system integrated with flywheel energy storage［J］.Joumal of South China University of Technology:Natural Science Edition，2009，37(4):75-79.

［13］Varela F J，Stewart J.Dynamics of a class of immune networks.I.global stability of idiotype interations［J］.Journal of Theory Biology，1990，144(1):93-101.

［14］付冬梅，郑德玲.基于Varela 免疫模型的免疫控制器的设计与仿真［J］.北京科技大学学报，2007，29(增刊2):199-203.Fu Dong-mei，Zheng De-ling.Design and simulation of immune controller based on Varela immune model［J］.Journal of Beijing Science and Technology University，2007，29(Suppl 2):199-203.

［15］夏长亮，刘均华，俞卫，等.基于扩张状态观测器的永磁无刷直流电机滑模变结构控制［J］.中国电机工程学报，2006，26(20):139-143.Xia Chang-liang，Liu Jun-hua，Yu Wei，et al.Variable structure control of BLDCM based on extended state observer［J］.Proceedings of the CSEE，2006，26(20):139-143.

［16］Mo H W，Fu D M，Xu L F.Research of a kind of improved immune controller based immune network［J］.International Joumal of Intelligence Computing and Cybemetics，2010，3(2):310-333.