基于云核粒子群算法的图像配准研究

张俊娜，穆华平

(1.河南师范大学计算机与信息工程学院，河南新乡453007;2.鹤壁职业技术学院，河南鹤壁458030)

1 前言

图像配准是将不同时间、不同成像设备或不同条件下(天候、照度、摄像位置和角度等)从同一场景拍摄的两幅或多幅图像通过像素的空间特征点变换模型，进行匹配、叠加使两幅图像在相同的位置具有灰度上的最大相似度，达到最佳对准［1］，图像配准有相对配准和绝对配准两种，相对配准是一张图像作为参考图像，其他多张图像将与之配准，坐标系统可任意变换;绝对配准所有的图像相对于原来规划的网格来进行配准，实现坐标的统一。图像配准可用于分析图像之间的相似度，在航空影像自动制图、图像三维重构、计算机视觉、遥感融合、模式识别等领域都有重要应用。

目前基于灰度信息的方法利用图像灰度的统计信息来度量图像的相似程度，但是不能直接用于校正图像的非线性形变，算法需要处理的数据量大［2］;基于图像特征的配准算法，利用图像上某些显著特征点、线、区域为配准基元，实现两幅图像之间逐像素的配准，但是异质图像的配准则是像素级精度，高精度的配准则不足［3］;基于对图像的理解和解释的配准算法，能自动识别相应像点，具有极高的可靠性和精度，涉及智能算法并依赖于算法的提高［4］。智能算法方面，目前应用比较多的是粒子群算法和云计算，粒子群算法具有易于实现的优点，但是存在早衰、陷入局部极值缺点，云计算具有随机性又有稳定倾向性的特性，构成定性和定量相互间的映射［5］。

本文在粒子群算法的基础上，引入云模型算法，利用云模型中的云核实现粒子动态优化，通过正态云发生器产生新粒子代，欧几里得空间距离的最大值定义为云核影响半径，把图像配准过程中目标函数达到最小值问题转化为云核粒子群算法寻优问题，实验仿真得出配准后图像的满足视觉要求，位置与参考图像保持了一致。

2 云核粒子群算法描述

2.1 云模型

云模型最初由李德毅院士1995年在随机数学和模糊数学的基础上提出的定性和定量转换模型［6］。云模型其定义为:设t为一维或者多维论域u→[0，1]上的定性概念，u 到［0，1］的映射元素Ct(u)为u→Ct(u)，则Ct(u)是对定性概念t的确定度，Ct(u)在u上的分布称为云，每个Ct(u)是云模型的云滴［7］。当Ct(u)服从正态分布时，称为正态云模型，遵循正态分布规律的具有稳定倾向的随机数集［8］，由期望值 Ex、熵 En、超熵 He来表征，Ex 是云滴在论域空间分布的期望;En是定性概念的可度量粒度，反映了云的陡峭程度，越大云覆盖水平就越宽;He是熵的不确定性度量，由熵的随机性和模糊性共同决定，决定云滴的离散程度。这3个特征值把模糊性和随机性完全集成到一起，构成定性和定量相互间的映射［9］。

本文采用正向正态云发生器［10］，实现了在语言值表达的定性信息中获得定量的范围和分布规律，是一个前向的、直接的过程［11］。

2.2 粒子群算法

设粒子群规模为N，在一个D维的目标搜索空间中，群体中的第 i(i=1，2，...，N)个粒子位置表示为一个 D 维矢量:Xi=(xi1，xi2，…，xiD)T，第 i个粒子的飞翔速度［12］:Vi=(vi1，vi2，…，viD)T，i=1，2，…，N。粒子根据以下公式来更新其速度和位置:

粒子在飞行的后期会失去粒子多样性，同时早熟收敛于局部最优值［13］。

2.3 云核粒子群算法

采用正向正态云发生器产生云滴Ct(u)=，将粒子群体分成三个子群，每个群由不同的云核进行引导，同时对粒子分别采用不同惯性权重ω调整策略［14］。将数量为N的粒子群在迭代第k代时第j维的的平均适应值为，假设适应值大于favg的粒子求平均适应值得favg'，适应值小于favg的粒子求平均适应值得favg″，依据平均适应值划分三个子群为，这时惯性权重ω调整策略为:

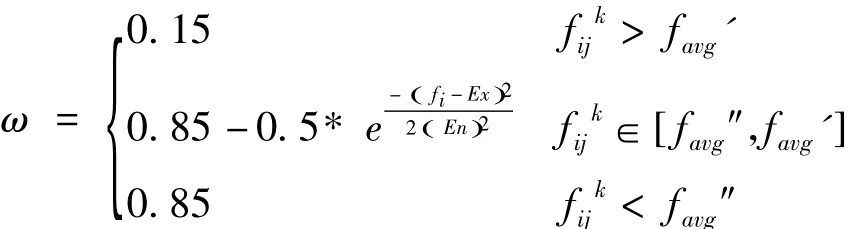
在三个子群中，对每个子群求出相应的平均适应值favgm，大于favgm粒子的平均适应值favgm'，适应值小于 favgm粒子的平均适应值 favgm″，其中 m=1，2，3，在三个子群中通过适应值的均方值分别作为引导云核，云核粒子引领子群内所有粒子到历史最佳位置pg的欧几里得空间距离的最大值定义为影响半径R:

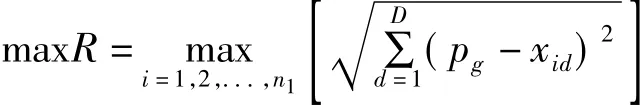
其中，n1+n2+n3=N，d是空间相同维度粒子的数目，对于在子群中影响半径以外的粒子，核粒子不再起引导作用［15］，这时粒子的更新方式为:

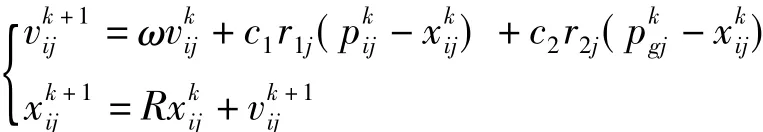
2.4 图像配准过程

假设参考图像和待配准图像在点(x，y)的分别定义为 Pi(x，y)、Qj(x，y)，图像的配准关系数学表示为:

其中，i是参考图像的第i个像素点;j是待配准图像的第j个像素点;f代表二维的空间几何变换函数;g是一维的灰度变换函数。

假设参考图像 Pi(x，y)和待配准 Qj(x，y)之间的欧式距离为:

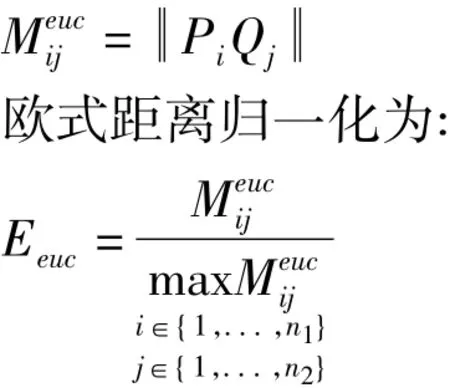
其中，n1为参考图像Pi(x，y)像素总数;n2为待配准Qj(x，y)像素总数。

配准图像的目标函数利用两副图像欧式距离归一化的差的平方和来表示:

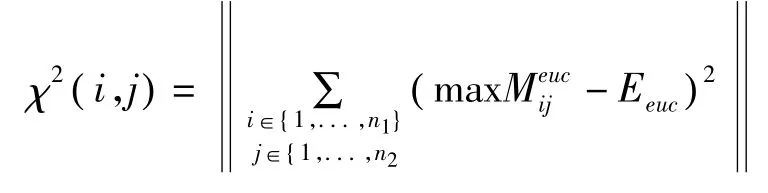
当参数向量(i，j)使目标函数达到最小值时，有:

这样把求解问题转化为云核粒子群寻优问题。

图像匹配的误差函数定义为:

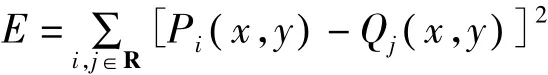
当E越小则配准越佳，本文设定阈值在0.0001。

算法过程为:

①输入一幅或者多幅图像，计算与参考图像像素的欧式距离;

②粒子群初始化，计算粒子初值以及适应值，依据云模型划分子群;

③云核引导粒子群更新粒子;

④计算误差函数，如果小于某一设定的阈值，则表示配准成功;若大于该阈值则转到步骤②;

⑤输出图像。

3 实验仿真

图像配准所用程序为 Matlab7.0，运行环境:CPU为3.6GHz，内存2048MB，操作系统XP，硬盘为SATA2接口，为了提高对比质量，下面的算法各进行30次蒙特卡罗仿真。图1是正态云滴参数为(20，4，0.5)生成可视化的云图。

图1 不同数量云滴的云模型视图

在图1中，不同数量云滴的反映了云的聚集度，越多则越聚集，无论聚集如何，靠近期望值中心或远离期望值中心处确定度的随机性变化较小，而离期望值中心不近不远的位置确定度的随机性变化大，这符合期望和熵的特点;中间云厚，两头云薄，这符合超熵的特点。

图2.1、图2.2和图2.3大小、分辨率相同，图2.1是参考图像，图2.2是待配准图对参考图像经过裁剪后得到的图像，图2.3是提取图2.2特征点的图像，提取待配准图的特征点利于图像的视觉效果以及误差对比，图2.4是配准结果图，从配准结果的视觉上看效果满足要求，配准后图像的位置与参考图像保持了一致，这是根据云核对粒子群的引导作用，粒子不再具有盲目性，而是跟随云核的移动，在粒子飞行上具有统一性，粒子位置更新由云核辐射半径影响，离云核越近，位置更新的随机性越小，而离云核越远，为了能够紧随云核粒子，粒子位置更新随机性越大，同时移动的位置范围也越大，使自己能够尽快的靠近云核，接受云核的辐射影响。

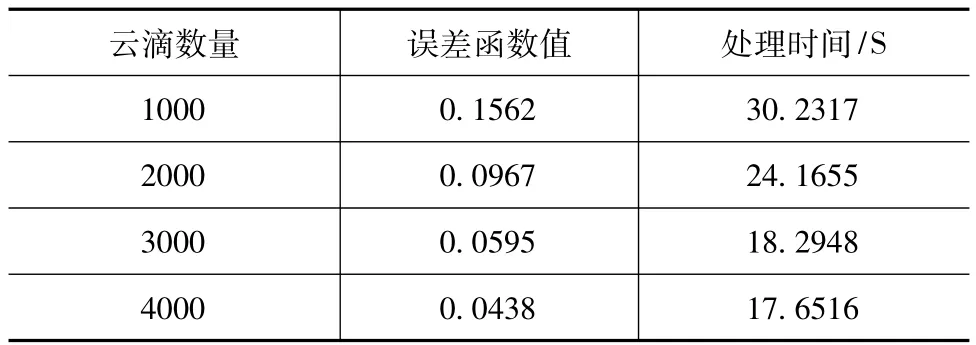
表1 不同数量云滴对配准的影响

在表1中，云滴数量越多，误差函数值值越小，处理时间越少，但是随着数量增加，其处理时间和误差函数值并不是成比例增加，比如在云滴数量3000到云滴数量4000的过程中，其性能增加没有云滴数量2000到云滴数量3000的过程中明显，这是因为云滴数量越多要求，云核粒子的辐射半径越大，而云核粒子的辐射半径无法覆盖全部子群的粒子，使半径以外的粒子不再具有引导作用，只是盲目性的寻优。

4 总结

文中结合云模型和粒子群优化算法的基本思想提出一种基于云核粒子群算法。在云模型中的云滴将粒子群体分成三个子群，对于在子群中影响半径以外的粒子，粒子核不再起引导作用。云核对粒子群的引导作用，粒子不再具有盲目性，而是跟随云核的移动，在粒子飞行上具有统一性。配准结果满足视觉上的要求，位置与参考图像保持了一致。

创新点:在云模型中引入正向正态云发生器;同时粒子群体分成三个子群，每个群由不同的云核进行引导，同时对粒子分别采用不同惯性权重ω调整策略。

［1］Li Wei，He Pengju，Yang Heng，et al．Genetic algorithm improvement for powell image registration［J］．Computer Engineering and Applications，2012，48(20):1 － 5．(in Chinese)

李伟，何鹏举，杨恒，等．遗传算法对Powell图像配准方法的改进［J］．计算机工程与应用，2012，48(20):1－5．

［2］Ye Miao．Image texture detection based on parallel gray level grade co－occurrence matrix［J］．Laser＆ Infrared，2011，41(11):1287 －1290．(in Chinese)

叶苗．基于并行灰度级差共生矩阵的图像纹理检测［J］．激光与红外，2011，41(11):1287 －1290．

［3］Liu Yu，Li Qiyu，Wang Xuezhen，et al．Fast video temporal alignment algorithm based on color characteristic［J］．Tv Engineering，2011，35(23):14 －16，43．(in Chinese)

刘昱，李器宇，王学珍，等．一种基于颜色特征的快速视频时域配准算法［J］．电视技术，2011，35(23):14－16，43．

［4］Shao Mingsheng，Wang Qihua．Blurred image restoration based on frog leaping algorithm［J］．Laser＆ Optoelectronics Progress，，2012，49(2):0210031 － 0210036．(in Chinese)

邵明省，王其华．基于蛙跳算法的模糊图像复原［J］．激光与光电子学进展，2012，49(2):0210031－0210036．

［5］Zhu Lin，Wang Shitong，Deng Zhaohong．Research on generalized fuzzy c-means clustering algorithm with improved fuzzy partitions［J］．Journal of Computer Research and Development，2009，46(5):814 －822．(in Chinese)

朱林，王士同，邓赵红．改进模糊划分的FCM聚类算法的一般化研究［J］．计算机研究与发展，2009，46(5):814－822．

［6］Li Deyi，Meng Haijun，Shi Xuemei．Membership clouds and ．Membership cloud generators［J］．Journal of computer research and development，1995，32(6):16 － 18．(in Chinese)

李德毅，孟海军，史雪梅．隶属云和隶属云发生器［J］．计算机研究与发展，1995，32(6):16 －18．

［7］Bruce A G，Gao Hongye．Waveshrink with firm shrinkage［J］．Statistica Sinica，1997，7(4):855 －874．

［8］Zhang Jinhua．Modified adaptive pso algorithm based on cloud theory［J］．Computer engineering and applications，2012，48(5):29 －31．(in Chinese)

张锦华．改进的云自适应粒子群算法［J］．计算机工程与应用，2012，48(5):29 －31．

［9］Liu Juan，Chen Huaping．Particle swarm optimization based on cloud model for scheduling single batch-processing machine with non-identical job sizes［J］．Computer systems ＆applications，2010，19(2):164 －168．(in Chinese)

刘娟，陈华平．基于云模型的PSO算法求解差异工件单机批调度问题［J］．计算机系统应用，2010，19(2):164－168．

［10］ Liu Dedi，Chen Xiaohong，Lou Zhanghua．Analysis on characteristics of spatial-temporal precipitation distribution based on cloud model［J］．Journal of hydraulic engineering，2009，40(7):850 －857．(in Chinese)

刘德地，陈晓宏，楼章华．基于云模型的降雨时空分布特性分析［J］．水利学报，2009，40(7):850 －857．

［11］ Li Deyi，et al．Artificial intelligence with uncertainty［M］．Beijing:National Defense Industry Press，2005:89 －130．(in Chinese)

李德毅，等．不确定性人工智能［M］．北京:国防工业出版社，2005:89－130．

［12］ Zhang Chaolong，Yu Chunri，Jiang Shanhe，et al．Particle swarm optimization algorithm based on chaos cloud model［J］．Journal of computer applications，2012，32(7):1951 －1954．(in Chinese)

张朝龙，余春日，江善和，等．基于混沌云模型的粒子群优 化 算 法［J］．计 算 机 应 用，2012，32(7):1951－1954．

［13］ Gong Minglang，Xu Rongsheng．On applying an improved pso algorithm in grid intrusion detection system［J］．Computer Applications And Software，2011，28(3):274 －278．(in Chinese)

龚明朗，许榕生．一种改进的PSO算法在网格入侵检测系统中的研究［J］．计算机应用与软件，2011，28(3):274－278．

［14］ Wei Xing qiong，Zhou Yong quan，Huang Huajua，et al．A-daptive particle swarm optimization algorithm based on cloud theory［J］．Computer engineering and applications，2009，45(1):48 －50，76．(in Chinese)

韦杏琼，周永权，黄华娟，等．云自适应粒子群算法［J］．计算机工程与应用，2009，45(1):48 －50，76．

［15］ Li Ning，liu Fei，Sun Baoguo．A study on the particle swarm optimization with mutation operator constrained layout optimization［J］．Chinese journal of computers，2004，27(7):897 －903．(in Chinese)

李宁，刘飞，孙德宝．基于带变异算子粒子群优化算法的约束布局优化研究［J］．计算机学报，2004，27(7):897－903．