基于蚁群算法的过程神经网络研究

2013-08-17李新东

哈尔滨商业大学学报（自然科学版） 2013年3期

葛利，李新东

(哈尔滨商业大学计算机与信息工程学院，哈尔滨150028)

过程神经网络[1]是传统神经网络在时间域上的扩展，具有较强的时变信息处理能力和非线性映射能力，对于大量过程式问题的求解具有较高的实用价值.其中应用最为广泛的是多层前馈神经网络模型，而基于BP算法训练的过程神经网络存在易陷入局部极小的缺点，为此本文提出一种蚁群过程神经网络模型，在分析蚁群算法与时变过程式输入特点的基础上，利用信息素和概率分布的方式，采用连续的信息素分布函数和概率分布函数代替传统的矩阵分布方式，将蚁群算法应用于前馈过程神经网络的训练，使得蚁群过程神经网络模型既具备过程神经网络的较强过程式信息处理能力，同时又具有蚁群算法的快速全局收敛能力[2－3]，并通过GDP预测问题验证了模型的有效性.

1 蚁群过程神经网络

1.1 过程神经元

过程神经元的结构由聚合、加权和激励运算三部分组成.它与传统神经元的区别在于:过程神经元的输入、输出和对应的权值均是时变的，其聚合运算既包含对空间的多输入聚合，也有对时间过程的累积聚合.单个过程神经元的结构如图1所示.其中:X(t)=(X1(t)，X2(t)，…Xn))T为过程神经元的输入函数向量，w1(t)，w2(t)，…wn(t)为相应的权函数，f(·)为激励函数，可取线性函数、Sigmoid函数、Gauss型函数等.

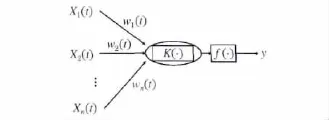
图1 过程神经元

过程神经元的输入、输出关系为

这里“⊕”表示某种空间聚合运算，“θ”为过程神经元阈值，“⊗”表示某种时间(过程)聚合运算，K(·) 为[0，T]上的一个可积函数[1].

1.2 蚁群过程神经网络的拓扑结构

双隐层蚁群过程神经网络模型的拓扑结构如图2所示.其中，第一层为输入层，共有n个节点单元，用以完成x1(t)，x2(t)……xn(t)n个时变函数向网络的输入;第二层为过程神经元隐层(第一隐层)，由m个过程神经元组成，完成对n个输入函数在空间和时间上的聚合运算，以及对样本特征的抽取;第三层为一般神经元隐层 (第二隐层)，由p个传统神经元组成;最后一层为输出层，其输出为常量y.

图2 蚁群过程神经网络的拓扑结构

该模型为一个多输入单输出的网络，拓扑结构为n－m－p－1.将蚁群过程神经网络各隐层需进化的网络权函数及权系数对应为蚂蚁待选择的路径数据，考虑到复杂输入、输出系统存在的非线性映射关系，在网络中增加了一个一般神经元隐层，以提高网络的整体非线性映射能力和适应性.

该网络各层之间的输入与输出关系为:

第1隐层输出:

第2隐层输出:

综合式(2)～(4)，则该网络输入与输出之间的关系为:

输出层:

式(2)～(5)中，wij(t)为输入层与过程神经元隐层的连接权函数，[0，T]为时间采样间隔，θj为第一隐层第j个神经元的输出阈值;vjk为第一隐层第j个神经元与第二隐层第k个神经元之间的连接权值，θk为第二隐层第k个神经元的阈值;yk为第二隐层与输出层的连接权值，f、g分别为第一隐层和第二隐层的激励函数，yj和yk分别为第一隐层第j个神经元的输出和第二隐层第k个神经元的输出，y为网络输出.此模型中空间聚合运算及时间聚合运算，可以根据实际问题选择其他形式的聚合算子[1，4].

1.3 蚁群过程神经网络的训练

1.3.1 蚁群过程神经网络的训练机制

蚁群过程神经网络的输入及时变隐层连接权均为时变函数的特点，使得蚁群过程神经元网络的映射机制和计算过程与一般非时变神经元网络有较大区别，其计算复杂度大大增加.同时由于网络连接权函数形式的任意性，在不对该函数加以一定的转化和处理的情况下，直接讨论过程神经网络的训练问题，权函数很难通过训练样本集的学习来确定.

设U是泛函空间S={f(x)|x=x(t)∈Rn，t∈R，f(x)∈V⊂Rm}上的一个紧致集，记C(U，V;n，m)为U到V上的连续映射泛函的集合.为讨论简单起见，取m=1，即多输入单输出系统(不难将结果推广到m＞1的情况).依据数学分析理论，蚁群过程神经元网络的权函数可表示为U中的一组基函数B(t)的展开式形式，即将权函数的形式限制在一类较为简单的函数类中来考虑问题.广义地讲，基函数B(t)既可以是有限基或可数基，也可以是正交基或非正交基.

为简化计算，本文在输入函数和权函数展开为输入空间同一组标准正交基函数的前提下，讨论蚁群算法的训练过程.权函数在标准正交基展开下的蚁群过程神经元的运算过程如下:

或一般地有

其中:b1(t)，b2(t)，……，bL(t)为U中的一组标准正交基函数，L为基函数的个数;w(l)i为wi(t)相对于bl(t)的展开式系数，θ为过程神经元的阈值，f为过程神经元的激励函数.K(·)可根据实际问题的需要来确定.

蚁群过程神经网络训练的基本思想为:将蚂蚁待寻优路径的数据设定为蚁群过程神经网络中待优化的参数，个数为n，其值为蚁群过程神经网络时变隐层权函数正交基展开式参数个数与非时变隐层权值个数之和.首先，将过程神经网络参数Pi(1≤i≤n)设置为N个随机非零值，形成集合Ipi.蚁群从蚁巢出发寻找食物，即每只蚂蚁在集合Ipi中选择一个权值，在全部集合中选择一组具体的数值.蚂蚁的数目为s，τ(Ipi)为集合Ipi(1≤i≤m)的第j个元素Pj(Ipi)的信息素.

蚂蚁相互独立地进行搜索并选择元素，当蚂蚁在所有集合中完成元素选择后，到达食物源，此时将每只蚂蚁所选择的元素集合，作为一组独立的蚁群过程神经网络参数，对蚁群过程神经网络进行训练，得到蚁群过程神经网络的一组实际网络输出，然后对比期望输出，得到对应的网络误差，并据此调节集合中元素的信息素，以减少网络误差.反复以上过程，当全部蚂蚁收敛到同一路径，或达到给定的迭代代数时训练结束.

1.3.2 蚁群过程神经网络的学习步骤

1)首先将蚁群过程神经网络权函数和输入函数表示为输入空间中同一组标准正交基的展开式，并初始化权函数展开式系数和非时变隐层权值.

2)令时间t和循环次数NC为零，设置最大循环次数NCmax，令每个集合中的每个元素的信息素τ(Ipi)(t)=C，其增加值Δτj(Ipi)=0;设定蚂蚁个数为s，过程神经网络的参数个数为n.

3)启动所有蚂蚁，对蚂蚁k(k=1，……，h)，根据路径选择规则(10)计算概率，用轮盘转法选择集合Ipi的元素.每只蚂蚁所选取路径，对应一组蚁群过程神经网络参数值.

路径选择规则:对集合Ipi，蚂蚁k根据公式(10)计算的概率Prob随机地选择它的第j个元素.

4)重复步骤3)，直到每只蚂蚁都选取到一组蚁群过程神经网络的参数，将各组参数，分别代入蚁群前馈过程神经网络，得到蚁群前馈过程神经网络的实际输出及网络误差，此时即蚁群已全部到达食物源.

5)令t←t+s，NC←NC+1将网络误差最小的一组参数，作为蚂蚁选择的最优路径，并记录当前最优解.

并依据下式规则调节信息素更新每个元素的信息素

其中:参数u(0≤u＜1)代表信息素的持久性，1－u对应信息素的消逝程度.Δτkj(Ipi)为第k只蚂蚁在本次循环中在集合Ipi的第j个元素Pj(Ipi)上留下的信息素，Δτkj(Ipi)值可依据不同情况获得:若第k只蚂蚁在本次循环中选择元素Pj(Ipi)，则信息素的增加值Δτkj(Ipi)依据式(12)来计算，否则信息素的增加值 Δτkj(Ipi) 根据式(13) 计算[2－3].

其中:Q为常数，用于调节信息素的调整速度;ek为将第k个蚂蚁选择的一组权值作为神经网络权值的输出误差，定义为ek=|O－Oq|.式中O和Oq是神经网络的实际输出和期望输出.

6)若蚂蚁群全部收敛至一条路径或循环次数NC≥NCmax，则训练结束，输出最佳路径作为最优解;否则转步骤(3).

2 蚁群过程神经网络的应用

以黑龙江省年度GDP预测为例，依据国家统计局网站上的1981～2009年的黑龙江省GDP相关数据作为原始数据，依据相关文献分析[5－8]，选取外贸出口总额、财政支出、社会消费品零售总额、实际利用外资、财政收入和固定资产投资作为影响GDP的6个主要因素，将其连续9 a的时序数据分别进行函数拟合，得到6个时变函数作为蚁群过程神经网络模型的输入，以下一个年度对应的黑龙江省GDP数值作为网络的期望输出，共组成21个样本.将其中的17个样本作为训练样本，4个样本作为测试样本.通过试凑法最终确定过程神经网络GDP预测模型的网络结构为6－17－1，即网络输入层节点数为6，输出层节点数为1，过程神经元隐层节点数为17.经过反复的测试和比较，最终确定蚂蚁数量s为25，常数Q为0.9，信息素的挥发系数u为0.6时，蚁群过程神经网络的训练取得相对理想的结果.

经878次迭代后网络收敛，4个测试样本对应的网络输出与其实际值对比结果如表1所示.从中可见，网络平均相对误差为3.89%.