建筑平屋面排水的数学模型及解答

丁 杰 周 清 刘海员 宋真真

(滨州市规划设计研究院，滨州 256600)

0 引言

屋面排水设计是建筑设计中一项非常重要的工作[1－7].合理的排水坡度可以使雨水顺利排入雨水管中，从而避免过度积水造成的屋面渗露或者破坏.对于建筑坡屋面，雨水可以沿着起坡方向汇入檐沟，然后，在檐沟中的雨水可以沿着指定的坡度汇入雨水管.但是，对于平屋面则要建筑师设定合理的排水坡度，同时借助于找坡层，才能使雨水按照合理的流线导入雨水管，因此，研究平屋面排水问题对于建筑师有着非常重要的意义.

1 屋面排水的基本要求

根据《屋面工程技术规范》(以下简称《技术规范》)与《民用建筑设计通则》，屋面排水方式主要分为内排水、外排水和组合排水[2].多数情况采用外排水，只有在外排水有困难时才会考虑使用内排水.屋面找坡方式通常分为材料找坡与结构找坡，本文主要讨论材料找坡的情况.

(1)对于排水坡度而言，从排水角度考虑，要求排水坡度越大越好.但从结构上、经济上及人们活动的角度考虑，则要求坡度越小越好.《技术规范》规定，当采用材料找坡时，排水坡度不宜大于2%[1].

(2)对于雨水管而言，雨水口或雨水管的间距应根据其排水能力、屋面和檐沟坡度等因素考虑决定，一般不宜大于24 m.并且雨水管径不得小于100 mm.汇水面积小于150 m2的屋面不宜只设一个雨水口.在同一汇水区域内，雨水立管不应小于两条，且负荷均匀.

(3)对于材料找坡层，建筑工程做法中最常采用的是水泥珍珠岩找坡层.根据以往学者研究结论[2－3]及工程经验可知，找坡层的最薄处不宜小于30 mm.

建筑是艺术与自然科学的结合体，优秀的建筑作品不仅在外观上给人赏心悦目的感觉，在内涵上更是闪烁着理性的光芒，这在建筑屋面排水设计上得以充分的体现.合理的排水坡度其本质上是如何将一个建筑学问题转化为数学问题来解决.国内外众多学者对建筑屋面排水都有过系统和深入的研究[6－7].本文将选择建筑设计中最常见的平屋面作讨论，结合以往学者的研究成果，按照数学方法建立数学模型，然后对数学模型加以解答，从而寻求排水问题的最优解.

2 矩形平屋面排水的数学模型及解答

矩形平屋面排水分为单坡排水与双坡排水.所谓单坡排水是指雨水沿着一个坡度汇入落水管，单坡排水适用于小面积屋面，多数的雨蓬、阳台顶面及连廊顶面等多设计为单坡排水.单坡排水设计简单，雨水沿固定坡度汇入落水管内，各点找坡层厚度可以通过排水长度与坡度相乘得到.同时，单坡排水可以看做双坡排水的一种特殊情况，本文主要讨论平屋面双坡排水.

平屋面双坡排水是屋面排水中应用最广泛、排水性能最好的一种排水方式.其原理是在一个方向起大坡(也叫主坡)，在另一个方向起小坡(也叫副坡).主坡是水流主向，副坡可以使其他方向的水流坡向主坡，主坡与副坡交汇在雨水管处，从而将屋面的雨水排出.

双坡排水可以利用副坡改变坡度的大小与方向，同时还可以根据实际需要改变副坡的起坡位置，所以排水方式较单坡排水灵活的多.正是基于此，在实际工程中，双坡排水一般可以设计成两种形式:一种是固定副坡排水坡度变化副坡起始位置;另一种是固定副坡起始位置变化副坡排水坡度.两种方法在数学解答上都是合理的.

图1 双坡排水建筑模型

图2 双坡排水数学模型

双坡排水的建筑模型如图1所示，主坡沿MN方向，主坡大小为i%，副坡分别沿ND与NC方向，排水坡度大小为iA%，iB%，雨水管设置在N点.与之对应的数学模型为图2，可以得到:

主坡与副坡的关系:

同时，O，P为主坡MN上的点，则有:

结合(1)～(3)式可以推导出方程:

同时，结合几何关系:

方程(4)可以表达为:

方程(6)表现为两种解答，也就是说双坡排水坡度通常可以设计为两种形式:

(1)当已知主排水坡度i%、副排水坡度iA%，iB% 时，方程(6)的解答为:

(2)当已知主排水坡度i%，副坡起始位置DE，CF时，方程(6)的解答为:

(7)，(8)式是在已知不同条件下的两种解答，其本质是一样的，并且两种解答都是正确的.

N点位于最底点，找坡层厚度应满足最小厚度:

各点的找坡层厚度为:

3 圆形(圆弧)平屋面排水的数学模型及解答

建筑师为了突出造型效果，往往把建筑物设计成各种形状.除了上面介绍的矩形屋面外，圆形(圆弧)屋面在现实生活中有着广泛的应用.

圆形平屋面与圆弧平屋面排水原理是一致的，圆弧平屋面可以看作圆形屋面的一部分.圆形(圆弧)平屋面的单坡排水平面可看作一个圆柱体(找坡层)被一个坡度很小的斜面(排水面)切割而成.同上述矩形单坡排水情况相似，起坡层厚度可通过流水的距离与排水坡度相乘得到.同时，单坡排水也可以看做双坡排水的特例.所以，本文主要讨论双坡排水的情况.同矩形屋面一样，圆形(圆弧)双坡排水的排水坡度仍然由大坡(主坡)和小坡(副坡)组成.主坡代表排水的主方向，副坡将不同方向的水导入主坡或者雨水管.

圆形双坡排水与矩形双坡排水原理大致相同，不同的是需要借助辅助线建立方程.图3为双坡排水的建筑图，i% 表示主坡，iA%，iB% 表示副坡，圆半径为R.为了求解，做辅助线GE，HF，FC，CE.图4为数学模型，可以得到:

图3 圆形平屋面双坡排水建筑图

图4 圆形平屋面双坡排水数学模型

主坡与副坡的关系:

并且:

同时，M点、N点是主坡上的点，那么有:

得到方程:

并且，同时:

方程(16)可以表达为:

式(18)从形式上与式(6)完全一致，这也说明圆形平屋面双向排水与矩形平屋面双向排水原理是一致的.同样，式(18)的解答表现为两种形式:

(1)当已知主排水坡度i%、副排水坡度iA%，iB% 时，方程(18)的解答为:

(2)当已知主排水坡度i%，副坡起始位置FH，EG时，方程(18)的解答为:

C点位于最底点，找坡层厚度应满足最小厚度

各点的找坡层厚度为:

4 工程综合算例

某屋面由圆形与矩形组合而成，圆形半径为2 m，其余尺寸如图5所示.雨水管位置如图5所示，设计此屋面排水.

解答:本工程采用单向双坡排水，需要联合利用矩形双向双坡排水与圆形双向双坡排水加以解答.由本文以上分析可知，本题同样存在两种解法:

解法一 假设主坡坡度为2%;副坡坡度分别为1.5%与1%，根据公式(7)及公式(19):

根据公式(9)～(12)及公式(21)～(25)，各个关键点的找坡层厚度为:

解法二 假设主坡排水坡度为2%，副坡起坡位置均为1.2 m，根据公式(8)及公式(20):

根据公式(9)～(12)及公式(21)～(25)，各点的找坡层厚度为:

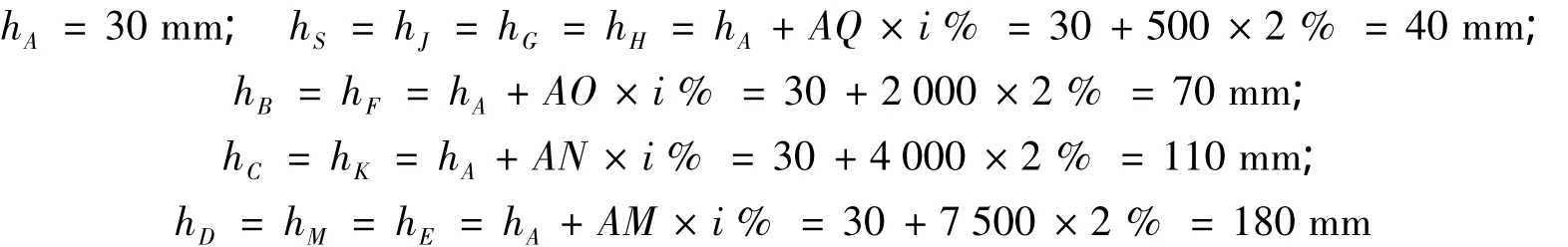
图5 算例解答一

图6 算例解答二

5 结论

建筑设计中的屋面形式各种各样，但其都是由基本元素(绝大多数情况为矩形与圆形)组成的.只要分析清楚其组成元素，并且借助于合理的数学方法，建筑师便可以设计出合理的排水方案，屋面排水问题即迎刃而解.

[1]屋面工程技术规范(GB50345－2004)[S].北京:中国建筑工业出版社，2004.

[2]民用建筑设计通则(GB50352－2005)[S].北京:中国建筑工业出版社，2005.

[3]徐国明.平屋面找坡层做法探讨[J].建筑技术，1997(6):49.

[4]黄慧芳.屋面找坡层标高的计算[J].山西建筑，2012，38(6):106 －107.

[5]杨焕利，王玉秋.平屋面排水设计新方案[J].鸡西大学学报，2005，5(1):68 －70.

[6]封 敏.大面积工业或公共建筑屋面雨水系统的选择[J].建筑施工，2005，27(7):66－72.

[7]张志利.屋面排水的细部构造及处理[J].山西建筑，2007，33(35):150 －151.