极差法在物理实验中的应用

申芳芳 陶荟春 满玉春

(吉林建筑大学基础科学部，长春 130118)

0 引言

物理实验课是高等理工科院校对学生进行科学实验基本训练的必修基础课程，是本科生接受系统实验方法和实验技能训练的开端.在《非物理类理工学科大学物理实验课程教学基本要求》中明确指出，大学物理实验教学内容要求学生具有正确处理实验数据的基本能力，能逐步学会用不确定度对直接测量和间接测量的结果进行评估[1].不确定度中A类不确定度的统计方法有多种，如贝塞尔法、灰色评定方法[2]、最大残差法、最小二乘法、最大误差法、分组极差法等等.国家计量技术规范JJF 1059—1999[3]中指出:“一般在测量次数较小时采用极差法”，“如果是正态分布(即要求测量次数大)的话用贝塞尔法”.现行的大学物理实验教材中一般都有关于不确定度知识的介绍，但对于A类不确定度的评定方法，几乎所有的教材都只讲贝塞尔法.在大学物理实验的实际测量中，对同一物理量的重复测量次数n不可能很大，一般小于5次，而当2≤n≤5时，贝塞尔法具有较大的误差[4].测量次数较少时，极差法是统计A类不确定度的有效方法.

本文以静态拉伸法测量金属丝杨氏弹性模量实验为例，用极差法对测量不确定度进行了估算，并与用贝塞尔法估算的结果进行了比较.

1 实验原理

设一根粗细均匀的金属丝长为L，横截面积为S，沿长度方向施力F后，其长度改变ΔL，则金属丝上各点的应力为F/S，应变为ΔL/L.根据胡克定律，在弹性限度内有:

则:

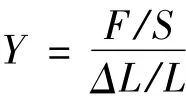
比例系数Y即为被测金属丝的杨氏弹性模量.

ΔL用光杠杆系统测量.如图1所示，光杠杆平面镜到标尺的距离为D，光杠杆常数为b，Δn为金属丝伸长前后在望远镜中看到的两个标尺像读数之差.则:

图1 光杠杆原理

设金属丝直径为，则:

有

2 实验数据

实验数据见表1，表2.

表1 测Δn数据记录

表2 测 L，D，b，d 数据记录

其中，L，D用钢卷尺测得，误差极限为0.1 cm;b用50分度游标卡尺测量，误差极限为0.002 cm;d用千分尺测量，误差极限为0.004 mm;标尺的误差极限为0.1 cm.

3 不确定度的估算

3.1 极差法

(1)A类不确定度

极差法[3]中A类不确定度U式中，极差R为测量列中最大测量结果与最小测量结果之差;系数C为极差系数.极差系数C的值与测量次数有关，表3给出极差法的极差系数与测量次数n的关系.

表3 极差系数

(2)B类不确定度

(3)不确定度计算

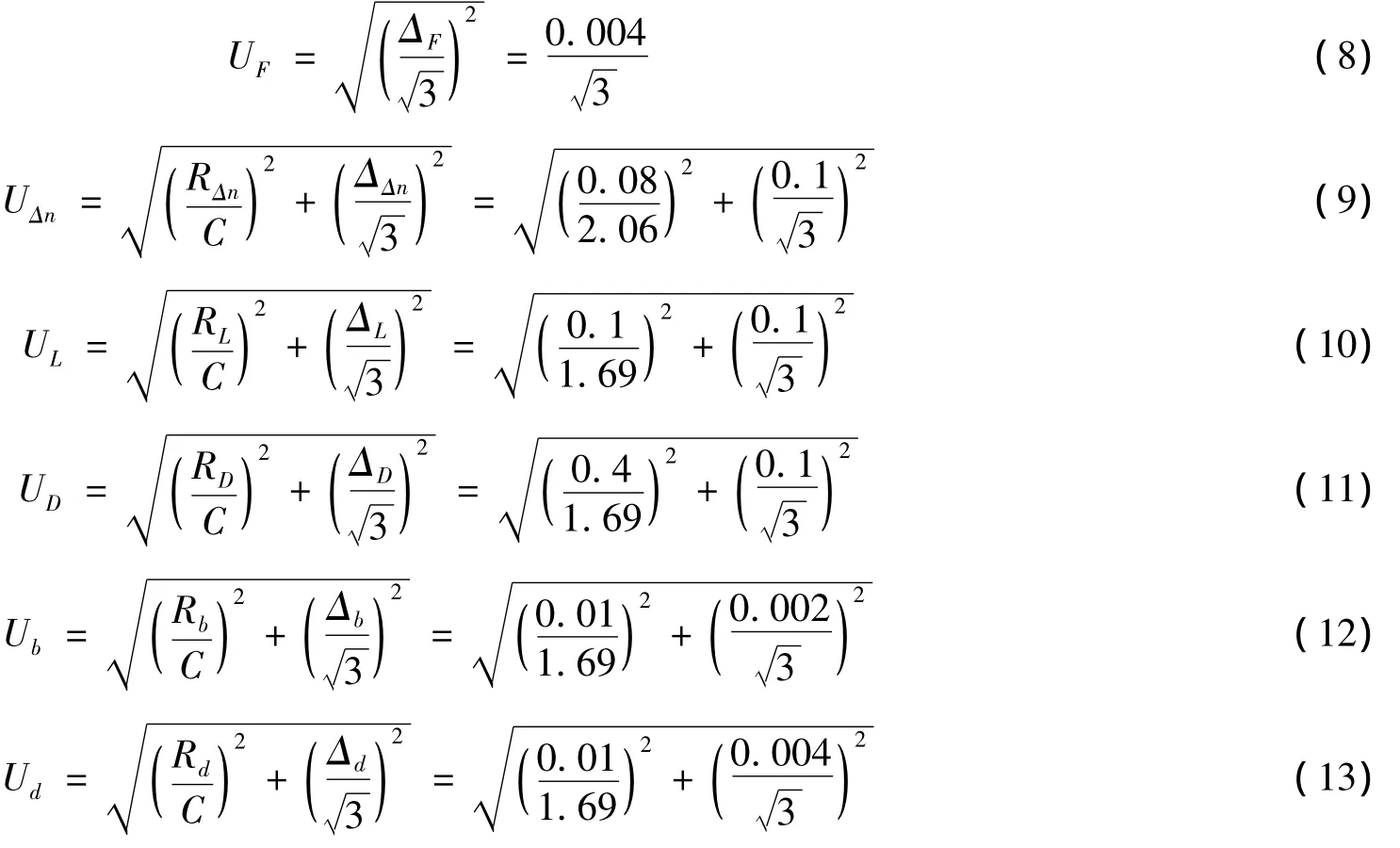
杨氏模量Y的相对不确定度为[6]:

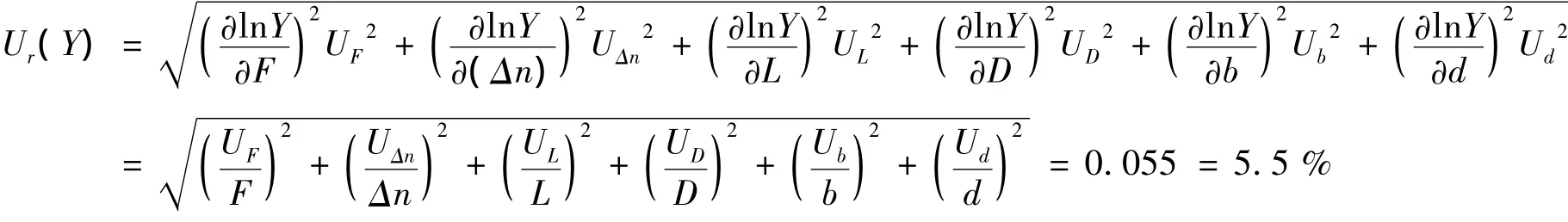
3.2 贝塞尔法

(1)A类不确定度

置信概率取95%时，t因子与测量次数n的对应关系见表4.

表4 A类不确定度的因子(p=95%)

(2)B类不确定度

同极差法，

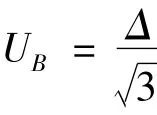
(3)不确定度

杨氏模量Y的相对不确定度为:

4 结论

由以上计算结果可以看出，用极差法计算A类不确定度时，结果的不确定度要小于用贝塞尔法计算出的不确定度，并且极差法的计算方法简单且容易理解和掌握.因此，在大学物理实验中应推广使用极差法来估算A类不确定度.

[1]教育部高等学校非物理类专业物理基础课程教学指导分委员会.非物理类理工学科大学物理实验课程教学基本要求(正式报告稿)[J].物理与工程，2006，16(6):1 －3.

[2]朱坚民，宾鸿赞，王中宇，周福章.测量结果标准不确定度的灰色评定方法[J].华中理工大学学报，2000，28(9):84－86.

[3]国家质量技术监督局.JJF1059－1999测量不确定度评定与表示[M].北京:中国计量出版社，1999:25－40.

[4]黄 琴，赵红玉，邓贤锋，孙小东，宋健辉.测量结果表示与A类不确定度的研究[J].计量与测试技术，2009，36(11):77－78.

[5]满玉春，陶荟春，宋晓东.大学物理实验[M].北京:北京邮电大学出版社，2011:6－7.

[6]李春贵.大学物理实验中A类不确定度探究[J].大学物理，2012，31(1):35－38.