铅镁铝合金热压缩变形条件对流变应力的影响及其本构方程的建立

2013-08-16何建洪段永华方东升

机械工程材料 2013年3期

何建洪，孙勇，段永华，方东升

（昆明理工大学稀贵及有色金属先进材料教育部重点实验室，材料科学与工程学院，昆明650093）

0 引言

铅基合金具有防射线、耐腐蚀等特点，可用来制备电缆套、电池板、轴瓦轴承及轴套等，在科研、军工、电力、交通、船舶、石化和建材机械中得到了广泛应用［1］。铅镁铝合金［2］作为铅基合金中的一种新型合金，其强度和硬度为235MPa和156HB，优于传统铅钙［3－4］或铅锑［5－6］合金的强度（最大30MPa）和硬度（最高13HB）。但铅镁铝合金塑性不高，这严重制约了它的成形和加工，故而提高其塑性加工能力成为当务之急。金属材料在热变形过程中常发生动态再结晶［7］，但目前还未见有关铅镁铝合金热变形方面的研究报道。为此，作者对铅镁铝合金进行了热压缩模拟试验，研究了其高温流变应力与温度、应变速率和应变之间的关系，并确定了其本构关系，为该合金的高温变形研究提供了理论参考。

1 试样制备与试验方法

试验所用材料为新型铅镁铝合金铸锭，其化学成分（质量分数／%）为49.95Pb，40.05Mg，10Al。将该铸锭加工成φ8mm×12mm的圆柱形压缩试样，要求试样表面光洁，两端面平行且光滑，没有裂纹等缺陷。采用Gleeble－1500型热模拟试验机进行热压缩试验，试验前在试样两端均匀涂敷含有石墨的固体润滑剂，以减少压缩时试样与压头之间的摩擦。

由于试验用铅镁铝合金的熔点约为698K，故选择变形温度分别为493，533，573，613K，压缩前试样以5℃·s－1的速率升温到变形温度，然后保温3min以保证试样内外温度均匀一致，之后进行压缩变形，应变速率ε·分别为0.01，0.1，1.0s－1，最大变形程度为40%。

2 试验结果与讨论

2.1 真应力－真应变曲线

从图1中可以看出，铅镁铝合金的真应力随着真应变的不断增加而增加到某一峰值后，就会逐渐下降到某一稳态值，曲线表现出明显的动态再结晶特征［8］。结合表1还可以发现，在其他变形条件相同时，真应力随温度的升高而下降，并随应变速率的增大而增大。因此，铅镁铝合金是一种正应变速率敏感材料［9－10］。

图1 不同应变速率下铅镁铝合金在热压缩变形时的真应力－真应变曲线Fig.1 True stress－true strain curves for Pb－Mg－Al alloy during hot compression deformation at different strain rates

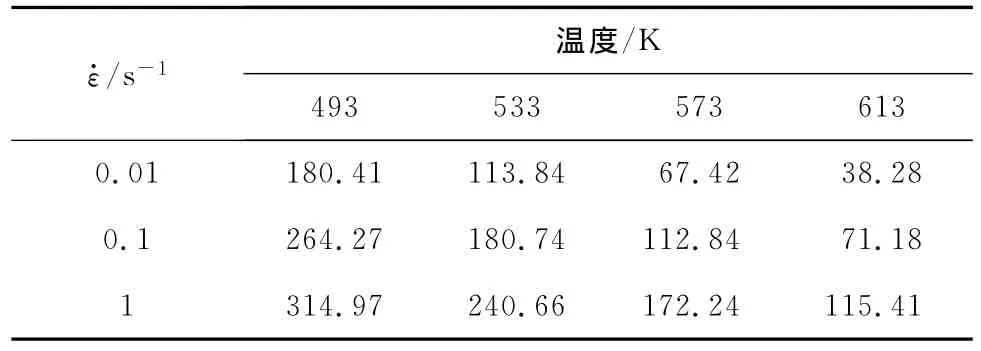
表1 不同应变速率和变形温度下铅镁铝合金在热压缩变形时的峰值流变应力Tab.1 Peak flow stresses of Pb－Mg－Al alloy during hot compression deformation at different deformation strain rates and temperatures MPa

2.1 变形条件对流变应力的影响

2.2.1 应变速率对流变应力的影响

目前有多种描述材料高温流变应力和应变速率的函数关系式。其中常用的主要有三种：指数关系式、幂指数关系式和双曲正弦函数关系式。现假设铅镁铝合金的高温峰值流变应力和应变速率满足上述关系式。

在低应力水平时，可以用指数关系式（1）来描述峰值流变应力和应变速率之间的关系；在高应力水平时，可以用幂指数关系式（2）来描述它们之间的关系；而双曲正弦关系式（3）适用于在所有应力水平下描述峰值流变应力和应变速率之间的关系。

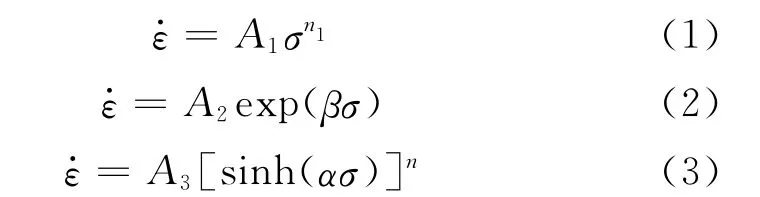
式中：σ为流变应力；A1，A2，A3和β均为与温度无关的常数；n和n1为应力指数；α为应力水平参数。

从目前研究成果可以看出，式（1）～（3）较好地描述了热变形过程中应变速率和流变应力之间的关系，可以用来计算应变、给定应变速率下的流变应力。分别对式（1）～（3）两边取对数，可得

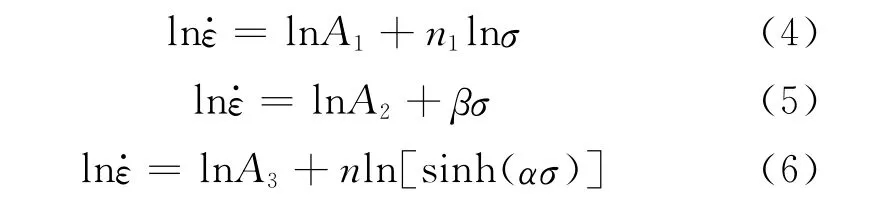
在不同的温度下，将表1中的峰值流变应力分别代入上述公式中，可以得到、l和ln［sinh（ασ）］之间的关系曲线，如图2所示。

从图2可以看出，三种曲线均为一元线性回归关系，各温度条件下的试验数据与回归直线吻合较好。通过一元线性回归方程可以求出各式中的常数，其中n1，β和n分别为图2（a）～（c）中各直线斜率的平均值。各温度条件下的一元线性回归方程列于表2中，其中，α＝β／n1。

图2 不同温度下铅镁铝合金峰值流变应力与应变速率之间的关系Fig.2 Relationship between peak flow stress and strain rate of Pb－Mg－Al alloy at different temperatutes

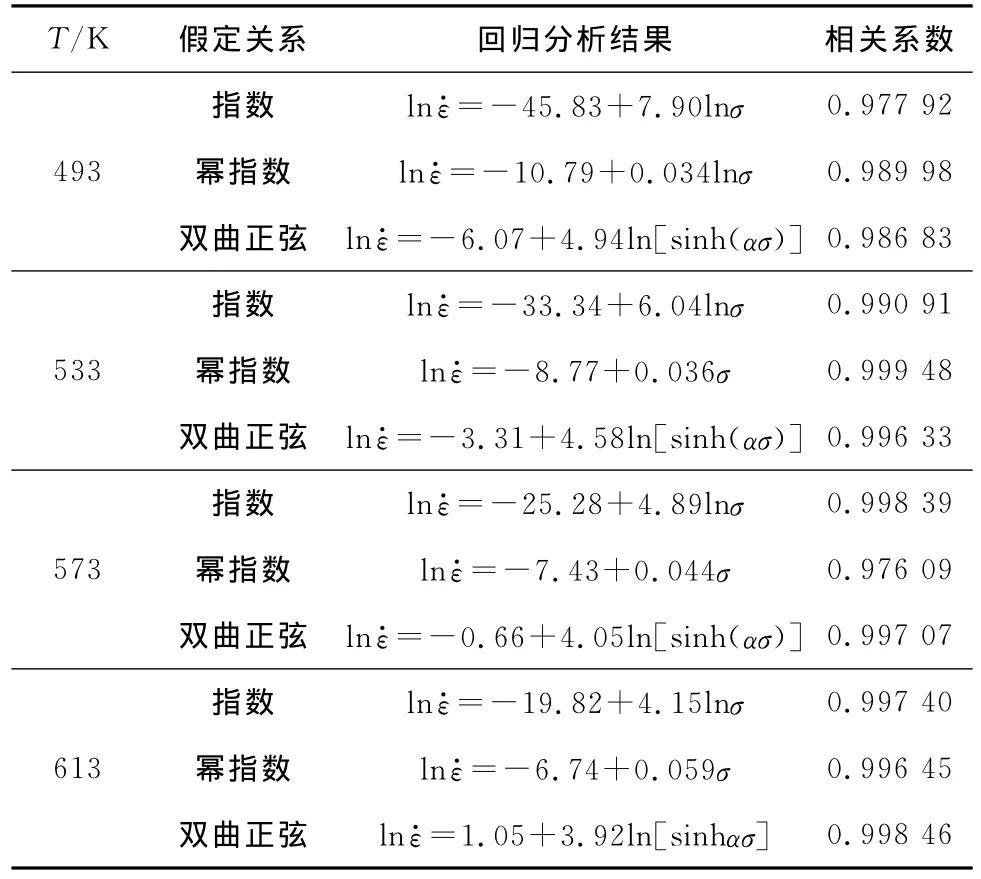
表2 铅镁铝合金流变应力与应变速率关系的回归结果（α＝0.006）Tab.2 Regression results of the relationship between flow stresses and strain rates for Pb－Mg－Al alloy

从表2可知，3种关系的相关系数都大于0.976。由此可以认为，铅镁铝合金材料高温热压缩变形时的流变应力和应变速率之间的关系都满足上述3式。其中，以双曲正弦关系符合得最好。

2.2.2 变形温度对流变应力的影响

在金属材料热变形过程中，变形温度对金属材料热变形时的流变应力有非常重要的影响，它是金属材料热塑性变形的一个重要参数。通常，在高温下金属材料的位错滑移阻力减小，新的滑移不断产生；同时，金属材料还发生回复、再结晶，能减小或消除塑性变形所产生的加工硬化，从而使流变应力降低［11］。另外，在变形中，大部分变形能转化为热能，也使材料内部温度发生变化，这也影响了金属材料的流变应力。Zener和 Hollomon指出［12－13］，应力－应变速率之间的关系可用Z参数表示：

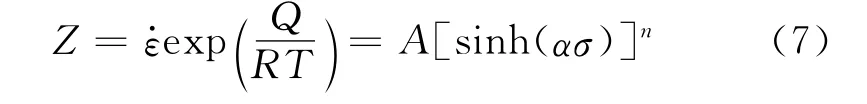
对式（7）两边取自然对数，整理后得

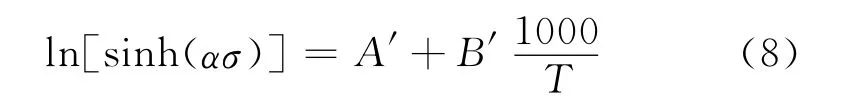
式中：Q为材料的热变形激活能；R为摩尔气体常数；T为热力学温度；A为与温度无关的常数；A′＝－lnA）／n；B′＝Q／（1 000 nR）。

将表1中不同变形条件下的峰值流变应力代入式（8），并进行一元线性回归分析，得到相应的ln［sinh（ασ）］－1 000／T 的关系图，如图3所示，其回归结果如表3所示。

从图3和表3可以看出，峰值流变应力的双曲正弦对数项与绝对温度倒数之间满足线性关系。由此可知，可用Z参数描述铅镁铝合金高温压缩变形时的流变应力，同时也表明铅镁铝合金的高温压缩变形受热激活能控制［14］。

2.3 本构方程的建立

从上述可知，铅镁铝合金的流变应力符合上述多种关系。但是，这些关系没有反映温度、应变速率和应变对流变应力的综合影响。因此，为了更好地研究铅镁铝合金热变形流变应力随应变速率、变形温度和应变的变化规律，为数值模拟提供可靠的参数，有必要确定铅镁铝合金高温变形时的流变应力本构模型。

采用Zuzin等［15］提出的高温稳态流变应力关系模型

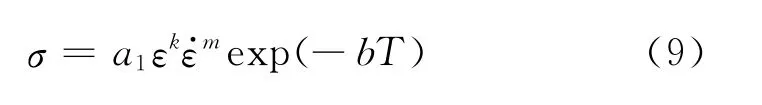
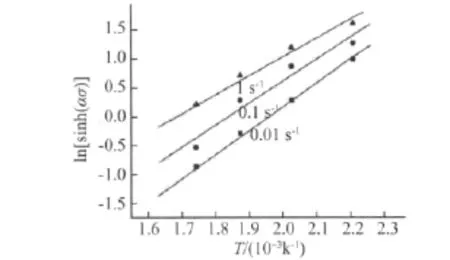
图3 铅镁铝合金峰值流变应力与温度之间的关系Fig.3 Relationship between peak flow stress and temperature for Pb－Mg－Al alloy

式中：k为硬化指数；m为应变速率敏感系数；b为温度系数；a1为系数；ε为真应变。

采用多元线性回归，确定式（9）中的各参数。

对（9）式两边同时取自然对数，得

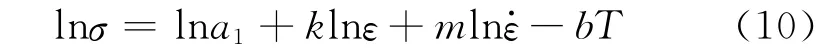
根据图1真应力－真应变曲线，取真应变在0.1～0.5之间的实测流变应力、变形温度、应变速率和真应变值进行多元线性回归分析，回归结果如表4所示。

从表4可知，铅镁铝合金的高温压缩稳态流变应力能较好地用式（9）表达，其复相关系数大于0.97。因此，得到铅镁铝合金高温压缩稳态时的本构方程如下：

表3 铅镁铝合金峰值流变应力与温度之间关系的回归结果Tab.3 Regression results of the relationship between peak flow stress and temperature for Pb－Mg－Al alloy

表4 铅镁铝合金稳态本构方程的多元线性回归结果Tab.4 Multiple regression of steady constitutive equation for Pb－Mg－Al alloy

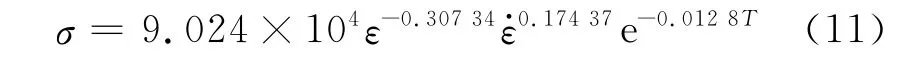
由回归分析结果可以看出，铅镁铝合金在高温稳态变形时，流变应力随应变速率的增加而增大；m值大于零，该合金为正应变速率敏感材料，这与前面的试验结果相吻合；应变硬化指数k小于零，这表明该合金在高温塑性变形稳态阶段，由于动态回复及动态再结晶等引起的位错密度降低的速度大于由应变硬化过程引起的位错的增殖速度，随着变形量增加，合金中的位错密度逐渐减小，合金发生软化，使合金的流变应力呈略减小的趋势，表现出近似稳态流变特征［16］。

利用式（11）对铅镁铝合金的稳态流变应力进行预测，并将实测值与预测值绘于图4中。图中曲线为实测值，散点为预测值。可见，实测值与预测值有较高的吻合精度，最大相对误差为11%，因此，式（11）能高精度地预测铅镁铝合金在高温热变形时的稳态流变应力。

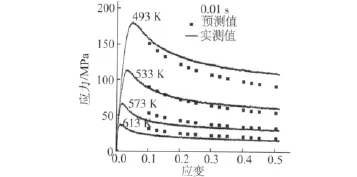
图4 流变应力预测值与实测值的比较Fig.4 Comparison between calculated and measured flow stresses

3 结论

（1）铅镁铝合金高温压缩变形时的流变应力和应变速率之间满足双曲正弦函数关系式。

（2）铅镁铝合金高温压缩变形时的流变应力可用Z参数描述，其高温压缩变形受热激活能的控制。

（3）铅镁铝合金高温热变形时稳态流变应力的本构方程为σ＝9.024×104ε－0.30734ε·0.17437e－0.0128T，该本构模型能高精度地预测铅镁铝合金在高温热变形时的稳态流变应力。

［1］李松瑞.铅及铅合金［M］.长沙：中南工业大学出版社，1996：148－329.

［2］DUAN Y H，SUN Y，PENG M J，et al.Mechanical and shielding properties of an as－cast new Pb－B shielding composite materials［J］.Advanced Materials Research，2011，150／151／56－63.

［3］ZHONG S，LIU H K，DOU S X，et al.Evaluation of lead－caleium－tin－aluminum grid alloys for valve－regulated lead／acid batteries［J］.J Power Sources，1996，59 （1）：123－126.

［4］龙秀全，黄履端.一种铅钙合金的制造方法：中国，CN－91106766.3［P］.1993－02－03.

［5］杨兰生，刘黎，潘颖辉，等.稀土铅锑合金的性能［J］.电源技术，1995，19（3）：15－18.

［6］MOSELEY P T.Lead／acid battery myths［J］.Journal of Power Sources，1996，59（1）：81－84.

［7］DUTTA R S.Development of Ni2Cr2Fe based steam generator tube materials［J］.Journal of Nuclear Material，2007（5）：1－6.

［8］SAKAI T，JONAS J J.Dynamic recrystallization：Mechanical and microstructural Considerations［J］.Acta Metall Mater，1984，32：189－209.

［9］罗迎社.金属流变成形理论、试验与应用研究［D］.上海：上海交通大学，2000.

［10］李俊鹏，沈健，许小静，等.7050高强铝合金高温塑性变形的流变应力研究［J］.稀有金属，2009，33（3）：318－322.

［11］郭强，严红革，陈振华，等.AZ31镁合金高温热压缩变形特性［J］.中国有色金属学报，2005，15（6）：900－906.

［12］SHI T，YU K，LI W X，et al.Hot－compression constitutive relaton of as－cast AZ31magnesium alloy［J］.Trans Nonferrous Met Soc China，2007，17：336－341.

［13］孙朝阳，刘金榕，李瑞，等.Incoloy 800H高温变形流动应力预测模型［J］.金属学报，2011，47（2）：191－196.

［14］黄裕金，陈志国，舒军，等.2E12铝合金的高温塑性变形流变应力行为［J］.中国有色金属学报，2010，20（11）：2094－2100.

［15］ZUZIN W I，BROWMAN M Y，MELIKOV A F.Metallurgy［M］.Moscow：［s.n］，1964.