内部算子空间及其范畴

杜银玲，卢 涛，朱润秋

(淮北师范大学 数学科学学院，安徽 淮北 235000)

范畴是从数学的各个领域中概括出来的一个高度抽象的数学系统，范畴理论的概念和方法对于解释和阐述抽象概念，确定科学研究框架起重要作用.在拓扑学中，由算子诱导出的拓扑空间是一类很重要的拓扑空间，内部算子作为重要的算子起很关键的作用.文献[1-2]表明，对于某一集合而言，其内部运算和拓扑是一一对应的.另外，崔艳丽和吴洪博[3]把拓扑空间上的闭包算子成功推广到闭包算子空间，并进一步研究其范畴性质.基于对这些知识背景的思考和启发，通过对拓扑空间上的内部算子及其性质的研究，引入内部算子空间，结合范畴理论去讨论内部算子空间范畴.本文通过对拓扑空间上的内部算子及其性质的研究，给出内部算子空间及其之间的连续映射的定义，讨论以内部算子空间为对象及其之间的连续映射为态射而构成的内部算子空间范畴，并证明内部算子空间范畴中的(有限)积的存在性.

1 内部算子空间与连续映射

定义1.1 设 X是一非空集合，I:ξ(X)→ξ(X)是一集值映射，若 I满足条件:

(1)I(X)=X; (2)∀A，B∈ξ(X)，I(A∩B)=I(A)∩I(B);

(3)∀A∈ ξ(X)， I(A)⊆A; (4)∀ A∈ ξ(X)，I(I(A))=I(A).则称 I为 X上的一个内部算子，(X，IX)或 X为内部算子空间.

例1.1 设(X，τ)是一拓扑空间，P(X)为 X的幂集，I:P(X)→P(X)的具体定义为:∀A∈P(X)，I(A)=A°，则由文献[1]中内部运算性质知，I为 X上的一个内部算子.

例1.2 设 X是一非空集合，I0:ξ(X)→ξ(X)为一集值映射，如果对∀A∈ξ(X)，I0(A)=A，则 I0为 X上的一个内部算子.

定义1.2 设(X，IX)和(Y，IY)是两个内部算子空间，f:X→Y，如果 f为满射且对于∀A∈ξ(X)，IY(f(A))⊆f(IX(A))，则称 f是从(X，IX)到(Y，IY)的一个连续映射，简称 f连续.特别地，当 X=Y时，称 f为(X，IX)上的连续映射.

定理1.1 设(X，IX)，(Y，IY)，(Z，IZ)都是内部算子空间，则

(1)内部算子空间(X，IX)上的恒同映射 iX:X→X是一个连续映射;

(2)如果 f:X→Y和 g:Y→Z都是连续映射，则 g◦f:X→Z也是连续映射.

证明由定义1.2中的内部算子空间上的连续映射定义直接验证.

2 内部算子空间范畴及其积

定义2.1[4]一个范畴 C由以下内容组成:

(i)一个对象类 ob(C)，ob(C)的元称为 C中的对象.

(ii)一个态射类 Mor(C)，Mor(C)的元称为 C中的态射.对于 C中对象的每个有序偶(B，A)，对应有唯一的一个集合 Hom(B，A).

(iii)对于 C中对象的每个有序三元组(B，A，C)对应一个称为复合(或合成)的映射:Hom(B，A)×Hom(A，C)→Hom(B，C)，(f ，g)→g ◦f，则 g ◦f称为 f和 g 的复合(或合成).

要求 C中对象和态射满足下列公理:

(1)若(B，A)≠(D，C)，则 Hom(B，A)∩Hom(D，C)=Ø;

(2)若 f∈Hom(B，A)，g∈Hom(C，B)，h∈Hom(D，C)，则(f◦g)◦h=f◦(g◦h);

(3)∀ B∈ob(C)，∃ idB∈ Hom(B，B)使得∀ f∈ Hom(B，A)，∀g∈Hom(C，B)，有 f ◦idB=f，idB◦g=g，idB称为 B上的恒同态射.

定义2.2 以内部算子空间作为对象，并以内部算子空间之间的连续映射作为态射，构成的系统，我们称之为内部算子空间范畴.

注1 定理1.1、映射性质及定义2.1表明，内部算子空间范畴的定义是合理的.

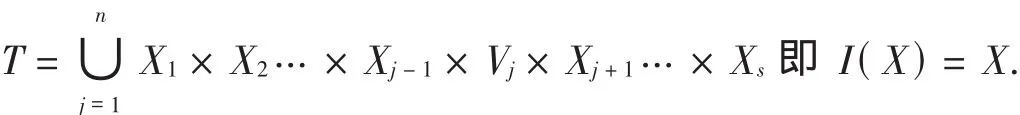
(2)对∀A∈ξ(X)，由定理2.1中的条件直接可得 I(A)⊆A;

(3)对∀A，B∈ξ(X)，令

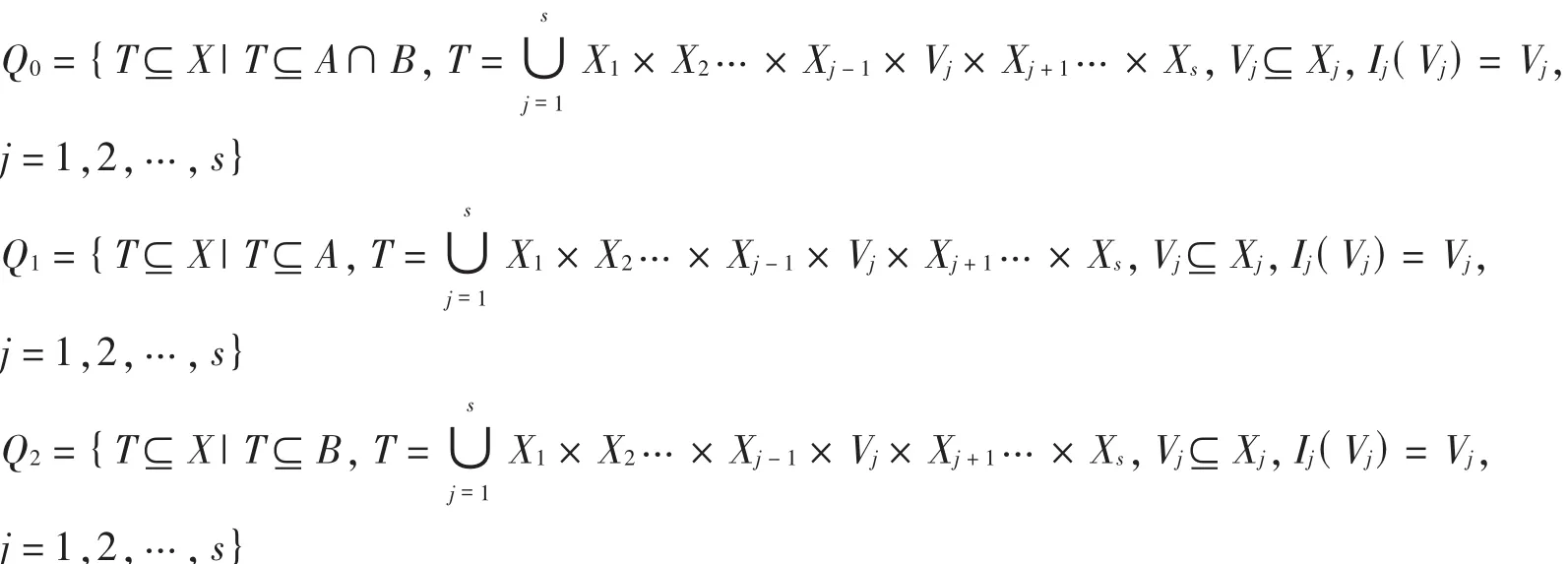
因为 Q0⊆ Q1， Q0⊆ Q2，从而∨ Q0≤(∨ Q1∧∨ Q2)，因此，我们得到 I(A∩ B)⊆ I(A)∩ I(B).而 I(A)∩ I(B)⊆I(A∩ B).故，I(A∩B)=I(A)∩ I(B).

(4)对∀ A∈ ξ(X)，另设

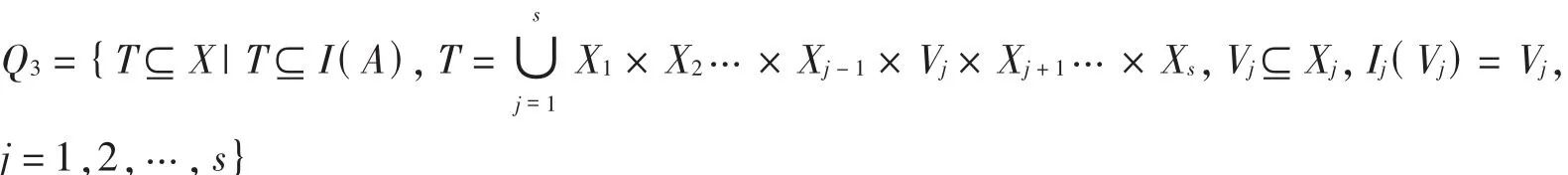
则 I(A)= ∨ Q1， I(I(A))= ∨ Q3.由(2)直接可得 Q3⊆ Q1，另有∀ T∈ Q1， T⊆ I(A)，则 T∈ Q3.故 Q1⊆ Q3，即 Q1=Q3，从而 I(I(A))=∨Q3=∨Q1=I(A).

综上(1)，(2)，(3)，(4)可知，I为 X 上内部算子.

注2 定理 2.1中的内部算子空间 X，对于每一个 i(i=1，2，…，s)，自然投射 Pi:X→Xi也为连续映射.

引理2.1[2]设(X，IX)和(Y，IY)是两个内部算子空间，那么映射 f:X→Y连续当且仅当∀B⊆Y，若 IY(B)=B，则 IX(f-1(B))=f-1(B).

定理2.2 设(X1，I1)，(X2，I2)，…，(Xs，Is)为 s(s≥1)个内部算子空间，(X，I)为定理 2.1 中所定义的内部算子空间，那么(X， I)是(X1，I1)，(X2， I2)，…，(Xs，Is)在内部算子空间范畴中的积.

证明假设(Y，IY)为任意一内部算子空间，对∀i≤s，gi:Y→Xi连续，Pi:X→Xi为自然投射.我们只需证∀i≤s，有唯一的连续映射 g:Y→X，使得 gi=Pi◦g.

(1)(下证 g 的存在性)定义 g:Y→ X，使得∀ y∈ Y， g(y)=(gi(y))i∈｛1，2，…，s｝，则有∀ i≤ s， gi=Pi◦g.对∀A⊆Y，若有

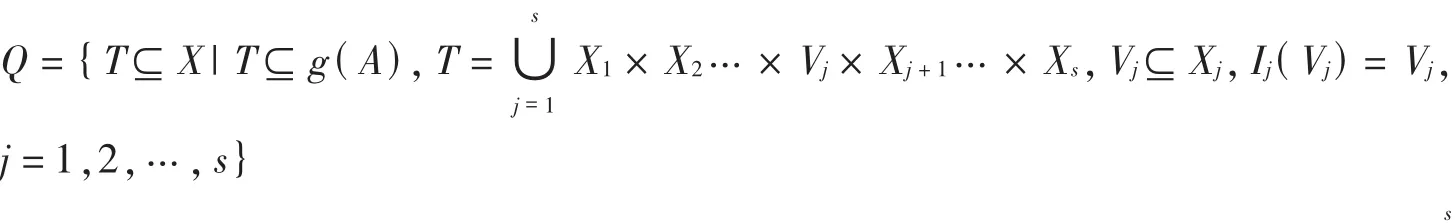
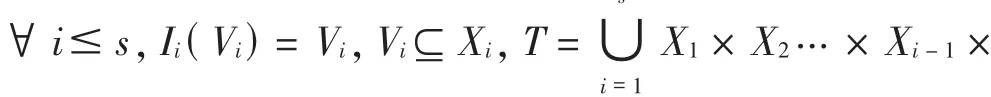
(2)(下证 g的唯一性)设另有连续映射 g＊:Y→X使得 gi=pi◦g＊，则∀i≤s，∀y∈Y，Pi(g＊(y))=gi(y)=Pi(g(y))，从而 g＊(y)=(Pi(g＊(y)))i∈｛1，2，…，s｝=(gi(y))i∈｛1，2，…，s｝=(Pi(g(y)))i∈｛1，2，…，s｝=g(y).由 y的任意性知 g＊=g.

综上(1)、(2)可知，(X， I)是(X1，I1)，(X2，I2)，…，(Xs，Is)在内部算子空间范畴中的积.

[1]熊金城.点集拓扑讲义[M].北京:高等教育出版社，1998.

[2]ENGLKING R.General topology[M].Warzawa:Polish Scientific Publishers，1977.

[3]崔艳丽，吴洪博.闭包算子空间范畴及其性质研究[J].计算机工程与应用，2010，46(27):54-56.

[4]郑崇友，樊磊，崔宏斌.Frame与连续格[M].2版.北京:首都师范大学出版社，2000.

[5]龚家安，吴洪博.内部算子与内部系统[J].南阳师范学院学报，2009，8(12):7-9.