拓扑系统的Lindelöf性质

杨 慧，姜广浩，肖 璨

(淮北师范大学 数学科学学院，安徽 淮北 235000)

1 预备知识

定义1.1[1]设 X 是集，A 是一frame，其最大元与最小元分别记为1，0.又设╞是 X× A 的子集，记(x，a)∈╞为 x╞a(读作 x 满足 a).若╞具有性质:

(1)对任一有限集 S⊆A和点 x∈X，x╞∧S 当且仅当每一 a∈S，x╞a;

(2)对任一集 S⊆A和点 x∈X，x╞∨S 当且仅当存在 a∈S，x╞a.

则称三元组(X，A，╞)为一拓扑系统.A 中的元称为拓扑系统的开元，X 中的元称为拓扑系统的点.通常用大写字母 D 表示拓扑系统(X，A，╞)，分别用 ptD和ΩD 表示拓扑系统 D 的点集 X和开元集 A.

定义1.2[2]设 D 是拓扑系统，X⊆ptD，≡是 ΩD 上的frame 同余.作 ΩD 上关于 X 上的等价关系≡x:∀ a，b∈ ΩD，a≡xb 当且仅当 a≡ b 且任意 x∈ X，x╞ a⇔ x╞ b，则≡x也为 ΩD 上的 frame 同余.此时拓扑系统 D' = (X，ΩD/≡X，╞)称为 D 的一个子拓扑系统，其中 x╞[ a]⇔x╞a.

定义 1.3[1]一簇拓扑系统｛Dλ｝的和系统∑λDλ定义为: pt∑λDλ= ∑λptDλ是点集的无交并，Ω∑λDλ=∏λΩDλ为 frame 的笛卡儿乘积，任意 x∈ ptDu，x╞〈aλ〉当且仅当 x╞ au.其中〈aλ〉∈∏λΩDλ.

定义1.4[1]拓扑系统 D和E 的积系统 D× E 定义为:

(1)pt(D × E)= ptD × ptE，

(2)Ω(D × E)= ΩD⊗ΩE 为 frame 张量积，

(3)(x，y)╞∨i(ai⊗bi)当且仅当存在 i 使得 x╞ai且 y╞bi.

定义1.5[1]设 D 是一个拓扑系统，任意开元 a∈ΩD 的内容 ex(a)定义为 ex(a)= ｛x∈ptD: x╞a｝.全体开元的内容形成 ptD 上的一个拓扑，记为 ΩptD，拓扑空间(ptD，ΩptD)称为 D 的空间化，记为 spatD.

定义1.6[1]设 D，E 是拓扑系统，D 到 E 的连续映射是指满足下列条件(1)- (3)的一对映射(ptf，Ωf)，记(ptf，Ωf)为 f: D→E.

(1)ptf: ptD→ptE 为映射;

(2)Ωf: ΩE→ ΩD 为 frame 同态;

(3)x╞Ωf(b)⇔ ptf(x)╞ b.

定义1.7[3]设 D 是拓扑系统，U，F⊆ptD.若存在 a∈ΩD，使 U= ex(a)，则称 U 为拓扑系统的开集.若存在开集 U 使得 F= ptD/ U，则称 F 为拓扑系统的闭集.

定义1.8[1-3](1)若任意一对点 x，y∈ptD，当 x≠y 时，存在 a∈ ΩD，使 x╞a 但 y╞a 不成立，或存在b∈ ΩD 使 y╞b 但 x╞b 不成立，则称拓扑系统 D 是 T0的.

(2)拓扑系统 D 称为 T1的，若任意一对点 x，y∈ptD，当 x≠y 时，有 a，b∈ΩD，使 x╞ a 但 y╞ a 不成立且 y╞b 但 x╞b 不成立.

(3)拓扑系统 D 称为 T2的，若任意一对点 x，y∈ptD，当 x≠y 时，有 a，b∈ ΩD，使 x╞a，y╞b 且 ex(a∧b)=Ø.

(4)拓扑系统 D 称为 T3的，若 D 是 T1的，且任意 x∈ptD，任意闭集 F⊆ptD，当 x∉F 时，有 a，b∈ΩD，使 x╞a，F⊆ex(b)，且 ex(a∧b)=Ø.

(5)拓扑系统 D 称为 T4的，若 D 是 T1的，且任意闭集 A，B⊆ ptD，当 A∩ B= Ø 时，有 a，b∈ ΩD，使A⊆ex(a)，B⊆ex(b)且 ex(a∧b)= Ø.

引理1.1[3]拓扑系统 D 是 Ti拓扑系统当且仅当 spatD 是 Ti拓扑空间，其中 i=1，2，3，4.

引入一个有用的记号∧C╞a.设 D 是拓扑系统，C⊆ptD，a∈ΩD.用记号∧C╞a 表示“∀x∈C，x╞a”.

定义1.9[1]设 D 是拓扑系统，点集 C⊆ptD，开元集 S⊆ΩD.若∧C╞∨S，则称 S 是 C 的一个开覆盖.若 C 的任意开覆盖有有限子覆盖，则称 C 是拓扑系统 D 的紧子集.进一步地，若 ptD 是拓扑系统 D 的紧子集，则称 D 为紧拓扑系统.

2 拓扑系统的Lindelöf性质

定义2.1设 D 是拓扑系统，点集 C⊆ptD，开元集 S⊆ΩD.若∧C╞∨S，则称 S 是 C 的一个开覆盖.称 C 是拓扑系统 D 的Lindelöf 子集，若 D 是 T3的，且 C 的任意开覆盖有可数子覆盖，即∧C╞∨S 蕴涵着存在可数子集 S0⊆ S 使得∧ C╞∨ S0.称 D 是 Lindelöf 拓扑系统或具有 Lindelöf 性质，若 ptD 是 D 的Lindelöf 子集.

定理2.1拓扑系统 D 具有Lindelöf 性质⇔拓扑空间 spatD 具有Lindelöf 性质.

证明⇒:设 S⊆ΩD 且 ptD⊆∪｛ex(a)| a∈S｝，则对∀x∈ptD，∃a∈S 使得 x╞a，故∧ptD╞∨S.由拓扑系统 D 具有 Lindelöf 性质知，存在可数子集 S0⊆S 使∧ptD╞∨S0，即对∀x∈ptD，∃a∈S0，使得x╞ a.从而 x∈ ex(a)⊆∪ ｛ex(a)| a∈ S0｝，进而 ptD⊆∪ ｛ex(a)| a∈ S0｝.由定义 2.1 知，spatD 具有Lindelöf 性质.

⇐:设 S⊆ ΩD 且∧ptD╞∨ S，则 ptD⊆∪｛ex(a)| a∈ S｝.由拓扑空间 spatD 具有 Lindelöf 性质知，存在可数子集 S0⊆S 使得 ptD⊆∪｛ex(a)| a∈S0｝.从而∧ptD╞∨S0.

推论2.1若 S⊆ ΩD 且任意可数集 S0⊆S 有∩｛ptD- ex(a)| a∈S0｝≠Ø，则

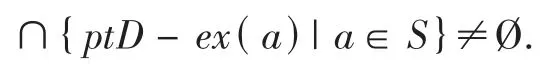
定义2.2[4]设 D'是拓扑系统的 D 的子拓扑系统.若 ptD'是 D 的闭子集，则称 D'为 D 的闭子拓扑系统.

定理2.2Lindelöf 拓扑系统的闭子拓扑系统是Lindelöf 拓扑系统.

证明设 D' = (ptD'，ΩD/≡，╞)是拓扑系统 D 的闭子拓扑系统，其中 ptD'是 D 的闭子集，≡是ΩD中关于 ptD'的 frame 同余.∀S'⊆ ΩD/≡，若∧ ptD'╞∨ S'，则对∀ α∈ S'，α≠Ø，由选择公理，设 S'上的选择函数 f(α)= aα∈ α⊆ ΩD.作 S= ｛aα| α∈S'｝⊆ ΩD.由子拓扑系统的性质易证，∧ ptD'╞∨ S.又 ptD'是 D 的闭子集，从而存在 b∈ΩD，使 ptD= ptD'∪ex(b)且 ptD'∩ex(b)=Ø，于是，∧ptD╞(∨S)∨b.由 D为 Lindelöf 拓扑系统知，存在 S 的可数子集 S0，使∧ ptD╞∨(S0∪｛b｝).注意到 ptD'∩ ex(b)= Ø，故任一x∈ ptD'，有 x╞∨ S0，即∧ ptD'╞∨ S0.作 S0'= ｛[ aα]| aα∈ S0｝.则 S0'是 S'的可数子集且在 D'中∧ ptD'╞∨S0'，由定义 2.1 知，D'为 Lindelöf 拓扑系统.

定理2.3可数个Lindelöf 拓扑系统的和系统是Lindelöf 拓扑系统.

证明设 D= ⊕t∈TDt，T 是可数集，且 ｛Dt｝t∈T具有 Lindelöf 性质.∀ S⊆ ΩD 若∧ ptD╞∨ S，由具有 Lindelöf 性质知，当∧ ptDi╞∨ Si时，∃可数子集，由定义 1.3 知即∧ptD╞∨S＊，其中为 S 的可数子集.

定理 2.4设 D 是 Lindelöf 系统，E 是紧拓扑系统，则 D × E 是 Lindelöf 系统.

证明若(x，y)∈ptD × ptE，(a⊗b)∈ ΩD × ΩE，(∧ptD，∧ptE)╞∨(a⊗b).由定义 1.4 知，∧ ptD╞∨a 且∧ptE╞∨b.由 D 是Lindelöf 系统知，存在可数子集 a0∈a 使得∧ptD╞∨a0，再由 E 是紧拓扑系统知，存在有限子集 b0∈b 使得∧ptE╞∨b0.即(∧ptD，∧ptE)╞(a0⊗b0)，得证.

定理2.5每个Lindelöf 拓扑系统都是 T4的.

证明设 D 是 T3拓扑系统，任意闭集 A，B⊆ ptD，A∩ B=Ø 且 A，B 具有 Lindelöf 性质.则∀ x∈ A，y∈ B，由 A∩B= Ø，再由 D 是 T2拓扑系统知，∃ ax，by∈ ΩD，使得 x╞ ax，y╞ by，且 ex(ax∧ by)= Ø.易知∧A╞∨｛ax| x∈ A｝，∧ B╞∨｛by| y∈ B｝.由 A，B 具有 Lindelöf 性质可知，存在｛ax| x∈ A｝的可数子集 ax1，存在 ｛by| y∈ B｝可数子集 by1，by2，…，bys0使得注意到 ex则∧ A╞ a，∧ B╞ b，且 ex(a∧ b)=Ø.

定理 2.6设 D 是 Lindelöf 系统，E 是 T3拓扑系统，f: D→ E 是满的连续映射，则 E 是 Lindelöf 系统.

证明设 S⊆ΩE，f(ptD)= ptE，ptf(ptD)╞∨S.由 f 的连续性及 Ωf 是 frame 同态，则∀x∈ptD，x╞Ωf(∨S)=∨Ωf(S)，从而∧ptD╞∨Ωf(S).由 D 是Lindelöf 系统知，存在 S 的可数子集 S0使得∧ptD╞∨Ωf(S0)，再由 f 的连续性知，∧ ptf(ptD)╞∨ S0，即∧ ptE╞∨ S0.再由定义 2.1 知，E 是 Lindelöf 系统.

引理 2.1[4]设 f= (ptf，Ωf): D→ E 是拓扑系统间的连续映射.任意 a，b∈ ΩE，a≡Ωfb⇔ Ωf(a)= Ωf(b).则(ptf(ptD)，ΩE/≡Ωf)是拓扑系统的子拓扑系统.

推论 2.2设 D 是 Lindelöf 系统，E 是 T3拓扑系统，f: D→ E 是满的连续映射，则(ptf(ptD)，ΩE/≡Ωf)是 Lindelöf 系统.

[1]VICKERS S J.Topology via logic [M].Cambridge: Cambridge University Press，1989.

[2]陈仪香.拓扑系统范畴与子拓扑系统[J].陕西师范大学学报:自然科学版，1994，22(4):19 -24.

[3]李世伦.拓扑系统的分离性[J].四川大学学报:自然科学版，2002，39(4):644 -648.

[4]李高林.拓扑系统的分离性，紧性和若干收敛结构[D].扬州:扬州大学硕士学位论文，2006.