基于优化BP神经网络的梁结构有限元模型修正*

胡俊亮 余晓琳 郑恒斌 陈舟 颜全胜，2†

(1．华南理工大学土木与交通学院，广东广州510640;2．华南理工大学亚热带建筑科学国家重点实验室，广东广州510640)

随着现代桥梁结构形式的多样化及复杂化，桥梁结构有限元模型在其计算分析过程中扮演着越来越重要的角色，研究人员投入了大量的精力到有限元模型的精细分析中．一般情况下，结构的固有特性通过现场试验与有限元模型分析两种方式来得到．尽管现场试验存在环境噪声的干扰、测量仪器的误差以及试验人员操作素养等因素而导致试验结果存在误差，但是，人们仍然可以认为现场试验得到的结果一定程度上能够反映结构的真实状况．因此，当现场测试结果与有限元模型分析结果不相匹配时，往往需要进行结构有限元模型修正，以期能模拟结构的真实状况．

Mottershead 和 Friswell［1］认为有限元模型不精确、与试验结果不相匹配的原因可归结于以下3个方面:①模型结构误差;②模型参数误差;③模型阶次误差．基于上述原因，研究人员将注意力转移到基于试验结果的有限元模型修正上．有限元模型修正方法大体可分为两类:整体结构矩阵型修正方法与参数型修正方法．

整体结构矩阵型修正方法首先由Berman等［2］提出:以有限元模型的质量矩阵M和刚度矩阵K的加权范数最小化为目标函数，以振型正交性和M、K对称性为约束条件，采用有约束的最小化求解方法进行模型修正．该方法应用了通过振动试验得到的结构特征向量与振型矩阵(经扩阶后的振型矩阵)．模型修正的精度直接与扩阶后的振型矩阵精度相关．且通过整体结构矩阵修正得到的结果将改变原有的结构矩阵带状、稀疏特性而成为满秩矩阵，甚至有些元素变为负值，导致得到的结构矩阵物理意义不明确．其后，众多研究人员根据存在的问题提出了他们的解决方法．Kabe［3］引入元素相关性的概念，提出了一种保持原模型结构矩阵带状、稀疏特性的方法;向锦武等［4］提出了通过求解结构矩阵的误差矩阵，定位误差较大的单元进行特定单元的修改，保持了原有结构矩阵特性．但这些方法存在的最大问题是经修正后的结构矩阵无法反馈到现有的通用有限元计算软件中，其适用性大打折扣．

参数型有限元模型修正方法选定特定的参数进行模型修正，使得有限元模型与试验结果误差最小．一般选择的修正参数有材料弹性模量、密度、构件截面面积等．通常情况下，若修正参数过多，将导致计算工作量过大．因此，基于灵敏度分析方法，找出较敏感的参数进行模型修正可以减少工作量．房长宇等［5］基于灵敏度分析，在贝叶斯理论中引入马尔科夫链-蒙特卡罗算法，提出了基于参数不确定性的有限元模型修正方法;韩芳等［6］提出了基于响应面的有限元模型改进方法．但基于灵敏度的模型优化方法存在这样一个问题:较敏感的参数不一定就是造成有限元模型误差的参数，这样修正后的有限元模型不一定能够反映结构的真实状况．因此，Hu等［7］在总结前人工作的基础上提出了不依赖于灵敏度分析方法的正交模型正交模态(CMCM)法．该方法在修正过程中试验模态可以与任意一阶分析模态进行组合，增加了修正方程的数量和待修正参数的个数，而不需要复杂的优化算法，极大地减少了计算工作量．但是，当修正对象的测试振型与分析振型相关性较好时，使用该方法会出现分母为零或接近零的数值病态问题．后续有众多研究人员针对参数型有限元模型修正方法做了改进，推动了参数型有限元模型修正方法的应用．韩大建等［8］进一步指出模型修正方法可以应用于结构损伤识别领域．文中采用非灵敏度分析参数型模型修正方法，提出基于遗传算法优化的BP神经网络方法进行模型修正，既能避免整体结构矩阵型修正方法的不足，又能综合平等考虑各参数对结构的影响．

1 基本原理

假设结构原始整体刚度矩阵为K，原始整体质量矩阵为M，则修正后的刚度矩阵、质量矩阵分别为

式中，ki、mi为第 i#单元刚度矩阵与质量矩阵，αi、βi为第i#单元弹性模量修正系数与密度修正系数．

为简化计算，减少待修正参数数量，将式(1)表达为

式中，α、β为结构整体弹性模量修正系数与密度修正系数．

设有限元模型得到的结构特征向量与振型矩阵为 、Φ．模型试验得到的结构特征向量与振型矩阵为*、Φ*．若采用测量振型矩阵作为目标函数，则需要将测量振型做扩阶处理，如此则会引入扩阶过程误差，且计算工作量较大．可采用特征向量误差作为目标函数，定义目标函数为

式中，x代表待优化参数，VLB为待优化参数上限值，VUB为待优化参数下限值，以文中算例来说，待优化参数包括结构材料弹性模量、密度以及边界条件模拟为弹簧的竖向刚度和抗弯刚度．式(3)通常采用优化算法进行迭代求解．文中采用基于遗传算法(GA)优化的BP神经网络方法进行求解．

2 基于遗传算法优化的BP神经网络

BP神经网络即误差反向传播神经网络，它是由非线性变换单元组成的前馈网络，其实质是求解误差函数最小值问题．近年来，BP神经网络因其结构简单，可调参数较多，训练算法也较多，可操作性好而在结构损伤识别领域得到了广泛的应用．Ko等［9］研究了采用神经网络进行信号处理的新颖滤波技术．Wu等［10］将BP神经网络用于建筑结构的损伤检测中．Povich等［11］用三层BP神经网络对一个20跨的平面桁架进行了损伤识别研究．孙宗光等［12］运用了动态网络和GA网络进行了桥面结构损伤位置识别，取得了较好的识别效果．宋玉普等［13］采用了基于模态应变能与神经网络的方法对一个空间钢网架进行了损伤位置和程度的识别工作，验证了其方法的有效性．

BP神经网络存在的学习收敛速度慢、不能保证收敛到全局最小值以及难以准确获得对网络训练影响重大的网络结构、网络初始权值和阈值等缺陷，使得其应用受到一定程度的局限．而上述问题一般可通过智能优化方法进行解决，消除该不足之后，BP神经网络强大的自主学习能力和优越的预测能力能够在有限元模型修正领域得到有效应用．运用优化算法对神经网络进行优化可以从两个方面开展:一是对网络结构进行优化，即主要确定隐含层数和各隐含层节点数;另一方面则是对网络初始权值和阈值进行优化．

对于大多数问题，三层BP神经网络已经足够，过多的隐含层在计算精度上并没有太大的提高，却要耗费更多的计算时间．隐含层节点数按一般经验:N1=2N2+1来选取．其中N2为输入层节点数，N1为隐含层节点数．对BP神经网络初始权值和阈值的优化则引入遗传算法来实现．

构造遗传算法优化BP神经网络的步骤如下［14］:

(1)随机生成BP神经网络初始权值和阈值，并采用二进制编码方式产生染色体P．每个个体由输入层与隐含层连接权值 W1，j、隐含层阈值 b1，j、隐含层与输出层连接权值W2，j、输出层阈值b2，j4个部分组成:P=［η，W1，W2，b1，b2］，η 表示隐含层层数，此时只有一层隐含层，W1为由连接权值 W1，1，…，W1，j，…组成的向量，W2为由连接权值 W2，1，…，W2，j，…组成的向量，b1为由阈值 b1，1，…，b1，j，…组成的向量，b2为由阈值 b2，1，…，b2，j，…组成的向量．

(2)选择神经网络预测样本预测值yt(k)与期望值^y(k)误差矩阵的范数作为目标函数的输出，即

式中，q为网络训练输入输出样本对个数，s为网络输出节点个数．

适应度函数采用Sheffield遗传算法工具箱中适应度分配函数:FitnV=ranking(obj)来取，其中obj为目标函数的输出．

(3)选用随机遍历抽样算子进行选择操作;交叉算子选择最简单的单点交叉算子;变异概率取为0．01，用随机方法选出发生变异的基因．

(4)得到的神经网络权值和阈值不满足误差要求，回到第(1)步．

(5)得到的BP神经网络权值和阈值满足误差要求，则训练新得到的BP神经网络，将实测连续梁模型特征值向量作为输入得到优化参数．

(6)将优化参数输入到有限元分析模型，若得到的分析频率不满足精度要求，则修改初始权值和阈值范围，重新进入第(1)步;当优化参数满足精度要求时，有限元模型优化结束．

具体流程图如图1所示．

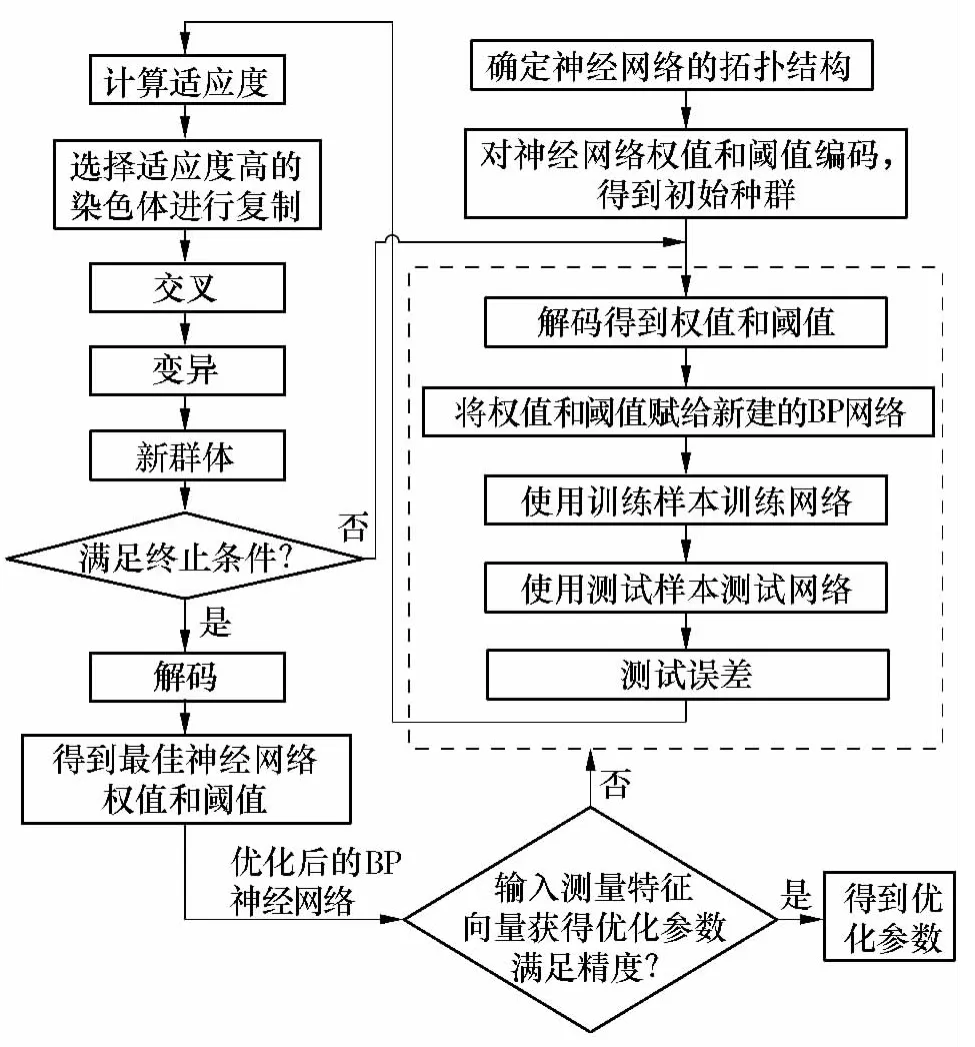
图1 基于遗传算法优化的BP神经网络流程图Fig．1 Flow chart of BP neural network optimized by genetic algorithms

3 算例

图2所示为混凝土连续梁模型结构，全长3800mm，采用 C35混凝土浇筑，分别在50、1050、2750、3750 mm位置进行约束，约束细部详见图3．采用有限元软件ANSYS建立该连续梁分析模型如图4所示．以3自由度梁单元 (UX，UY，RotZ)Beam3模拟连续梁体，以Combin14单元模拟竖向约束UY和绕Z轴弯曲约束RotZ．梁体分为38个单元，按照约束位置建立4个竖向弹簧单元、4个弯曲弹簧单元，并在第1个约束位置约束纵向DX自由度．将混凝土梁弹性模量E、密度ρ以及弹簧单元竖向刚度系数Ku和抗弯刚度系数Kr作为待修正系数．设其初始取值范围如表1所示．根据材料特性和工程经验设定合理的待修正参数取值范围可以大大降低寻优过程时间．

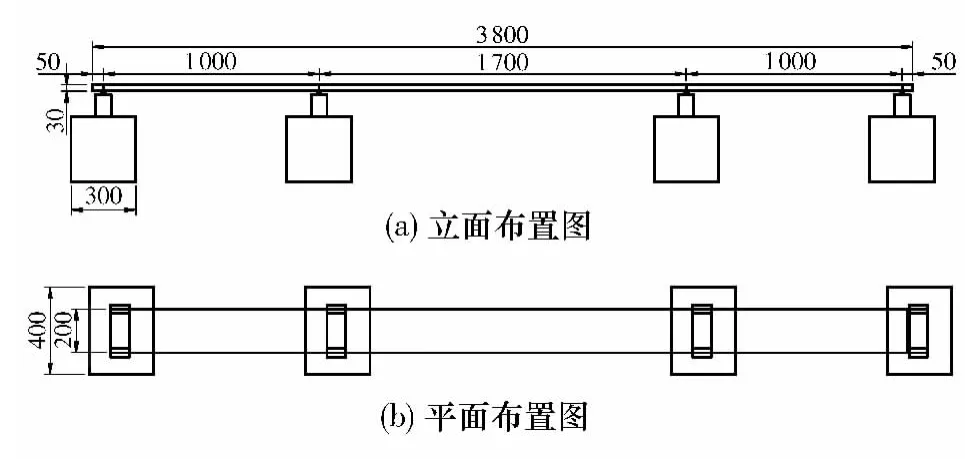
图2 连续梁结构示意图(单位:mm)Fig．2 Schematic diagram of structure of continuous beam(Unit:mm)

图3 连续梁约束细部图Fig．3 Details of continuous beam constraint

图4 连续梁有限元模型Fig．4 Continuous beam finite element model

3．1 模型修正

编制Matlab与ANSYS接口程序，选择上述范围内待修正参数50组随机数，分析得到50组结构频率．因实测结构模态为已知量，因此在进行神经网络学习时，将结构频率作为输入，待修正参数为输出．取前40组数据作为训练样本，后10组数据作为测试样本．由于待优化参数存在数量级上的差别，为平等考虑各优化参数，避免优化得到的BP神经网络权值和阈值的不稳定，将待优化参数的数值进行归一化处理后作为输出．得到经遗传算法优化后的BP神经网络权值和阈值后，训练BP神经网络．根据测试样本得到的结果发现，经50代遗传优化后遗传算法得到最优权值和阈值，优化BP神经网络算法误差降低到0．1%以下，满足结果精度要求．遗传算法迭代曲线如图5所示，BP神经网络训练误差性能曲线如图6所示．将实测频率作为输入得到神经网络输出结果，修正后的参数如表1所示．

图5 遗传算法遗传误差迭代曲线Fig．5 Error iterative curve of genetic algorithm

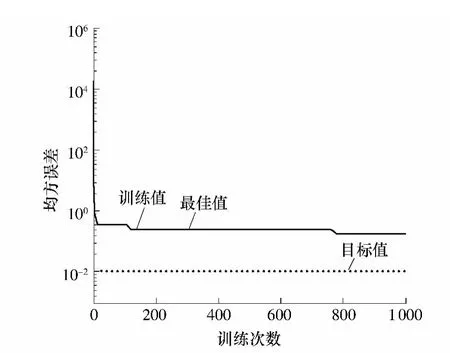
图6 BP神经网络误差变化曲线Fig．6 Error curve of BP neural network

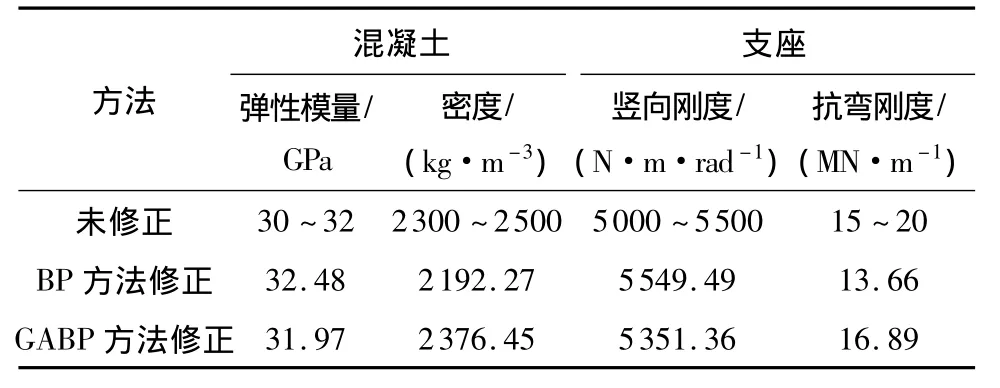
表1 修正参数对比Table 1 Modified parameters comparison

为避免高阶模态测量误差导致模型修正的误差，仅取前四阶频率作为模型修正目标函数的标准值．综合考虑优化算法的修正能力，分别按照未优化、BP算法优化、遗传算法优化的 BP神经网络(GABP)算法优化3种方式考虑模型修正结果．修正后频率对比见表2．当未进行任何优化时，前两阶频率与实测值接近，但是三、四阶频率误差在15%以上;当BP神经网络权值未采用遗传算法优化时，得到的修正模型计算频率误差在4%左右，整体精度有所提高，但是前两阶频率精度较未优化时反而有所降低;采用GA优化后的神经网络得到的修正模型分析频率误差在0．5%以下，精度得到了很大的提高．最重要的是，就本算例来说，采用GA算法对BP神经网络初始权值和阈值进行优化后，当预设相同计算精度时，GABP方法计算效率要高得多，可以达到直接BP修正方法的2倍以上。

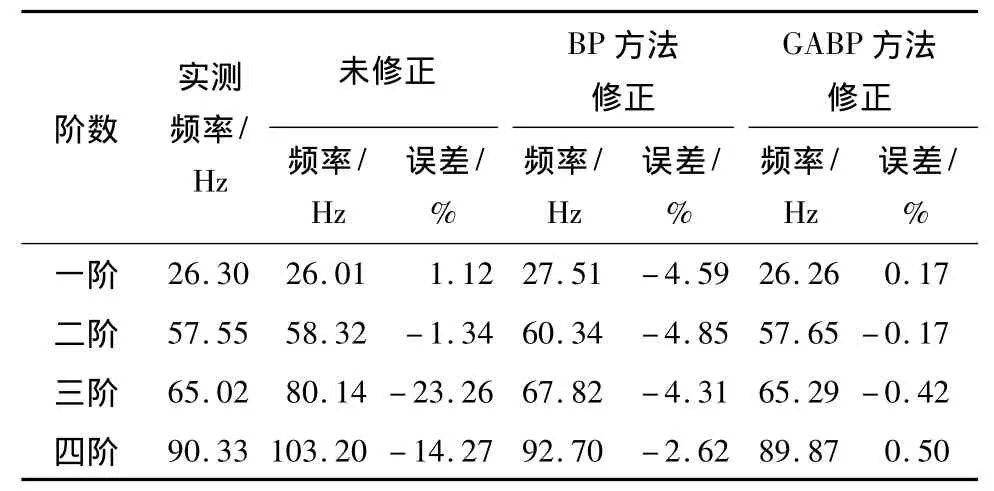
表2 修正后频率对比1)Table 2 Frequency comparison odter modification

3．2 模型修正验证

模态保证准则［15］利用振型的正交性来分析比较两个振型之间的关联性．最早被提出是评估试验模态特征向量质量的需要，后广泛应用于结构损伤识别领域［16-19］．文中利用MAC作为有限元模型修正的评价指标．当MAC矩阵的数值趋于0时，说明两个振型之间无相关性，当MAC矩阵数值趋于1时，说明两个振型之间完全相同．MAC矩阵的计算式如下所示:

各方法MAC值如表3所示．经过模型修正后MAC值对角数值均在0．9以上，特别是经过GABP方法修正后MAC矩阵对角数值均在0．94以上，说明修正后分析振型与测量振型具有高度相关性．

图7示出了测量振型与模型修正后计算振型的对比．为保证分析振型与测量振型数量级的一致性，按照振型比例系数［20］对各分析振型做预处理．从图7可知，第1、2阶振型各分析振型与测量振型吻合度较高，第3、4阶未修正模型分析振型与测量振型有较大差别，而BP修正模型与GABP修正模型分析振型与测量振型高度吻合．振型对比结果与频率计算结果具有类似的规律．

4 结论

文中提出了基于遗传算法优化的BP神经网络方法，对一个三跨连续梁试验模型进行了有限元模型修正，得到以下结论:

(1)修正后有限元模型的预测误差有了较大程度的降低，说明采用文中方法进行有限元模型修正具有较高的精度，MAC矩阵与振型对比结果同时说明了该方法的有效性;基于GA优化的BP神经网络计算效率有了较大的提高，能更快得到收敛结果;

表3 各方法MAC值列表Table 3 MAC values list of each method

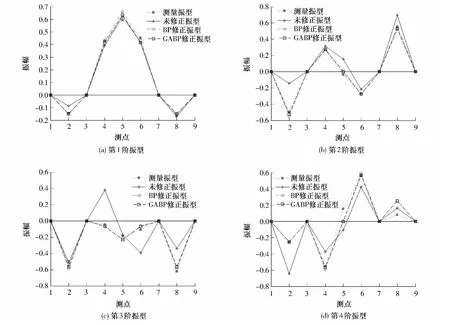
图7 前4阶振型对比Fig．7 The first 4 mode shapes comparison

(2)采用GA优化后神经网络结果显著高于采用随机权值和阈值的神经网络模型修正结果;

(3)对文中算例而言，仅考虑全局参数的优化就得到满足精度要求的修正有限元模型，说明在大部分情况下，不必以单元尺度来进行参数优化，这样可大大降低计算工作量;

(4)根据频率对比与振型对比结果发现，GABP修正方法得到的频率较BP修正方法有较大的提高，而二者振型并没有明显的差别，说明了振型测量的不敏感性，因此，在进行模型修正时可以较敏感的频率而非位移振型作为修正的目标函数．

［1］Mottershead J E，Friswell M I．Model updating in structural dynamics:a survey ［J］．Journal of Sound and Vibration，1993，167(2):347-375．

［2］Berman A，Flannelly W G．Theory of incomplete models of dynamic structures［J］．AIAA，1971，9(8):1481-1487．

［3］Kabe A M．Stiffness matrix adjustment using mode data［J］．AIAA，1985，23(9):1431-1436．

［4］向锦武，周传荣，张阿周．基于建模误差位置识别的有限元模型修正方法［J］．振动工程学报，1997，10(1):1-7．Xiang Jin-wu，Zhou Chuan-rong，Zhang A-zhou．Modification of finite element model based on identified error locations［J］．Journal of Vibration Engineering，1997，10(1):1-7．

［5］房长宇，张耀庭．基于参数不确定性的预应力混凝土梁模型修正［J］．华中科技大学学报:自然科学版，2011，39(11):87-91．Fang Chang-yu，Zhang Yao-ting．Model updating of prestressed concrete beams using parameters uncertainty［J］．Journal of Huazhong University of Science and Technology:Natural Science Edition，2011，39(11):87-91．

［6］韩芳，钟冬望，磨季云．基于改进响应面法的结构模型修正研究［J］．武汉理工大学学报:交通科学与工程版，2012，36(1):196-198．Han Fang，Zhong Dong-wang，Mo Ji-yun．Research on model updating based on improved response surface method［J］．Journal of Wuhan University of Technology:Transportation Science ＆ Engineering，2012，36(1):196-198．

［7］Hu S L，Li H J，Wang S Q．Cross-model cross-mode method for model updating［J］．Mechanical Systems and Signal Processing，2007，21(4):1690-1703．

［8］韩大建，王文东．基于振动的结构损伤识别方法的近期研究进展［J］．华南理工大学学报:自然科学版，2003，31(1):91-96．Han Da-jian，Wang Wen-dong．Overview of vibration-based damage identification methods［J］．Journal of South China University of Technology:Natural Science Edition，2003，31(1):91-96．

［9］Ko H，Baran R，Arozullah M．Neural network based novelty filtering for signal detection enhancement［C］∥Proceedings of the 35thMidwest Symposium on Circuits and Systems．Washington D C:IEEE，1992:252-255．

［10］Wu X，Ghaboussi J，Garrett J H．Use of neural networks in detection of structural damage［J］．Computers ＆Structures，1992，42(4):649-659．

［11］Povich C R，Lim T W．An artificial neural network approach to structural damage detection using frequency response functions［C］∥Proceedings of the 1994 AIAA/ASME Adaptive Structures Forum．Washington D C:American Institute of Aeronantics and Astronautics，1994:151-159．

［12］孙宗光，高赞明，倪一清．基于神经网络的桥梁损伤位置识别［J］．工程力学，2004，21(1):42-47．Sun Zong-guang，Gao Zan-ming，Ni Yi-qing．Identification of damage location in bridge deck by neural network［J］．Engineering Mechanics，2004，21(1):42-47．

［13］宋玉普，刘志鑫，纪卫红．基于模态应变能与神经网络的钢网架损伤检测方法［J］．土木工程学报，2007，40(10):13-18．Song Yu-pu，Liu Zhi-xin，Ji Wei-hong．Damage diagnosis of spatial trusses based on modal strain energy and neural network ［J］．China Civil Engineering Journal，2007，40(10):13-18．

［14］史峰，王辉，郁磊，等．MATLAB智能算法30个案例分析［M］．北京:北京航空航天大学出版社，2011．

［15］Allemang R J，Brown D L．A correlation coefficient for modal vector analysis［C］∥Proceedings of International Modal Analysis Conference．Orlando:SEM，1982:110-116．

［16］George H，Rene B Testa．Modal analysis for damage detection in structure［J］．Journal of Structural Engineering，1991，117(10):3042-3063．

［17］Wahab M M A，Roeck G D．Damage detection in bridges using modal curvatures:application to a real damage scenario［J］．Journal of Sound and Vibration，1999，226(2):217-235．

［18］Yan Y J，Cheng L，Wu Z Y，et al．Development in vibration-based structural damage detection technique［J］．Mechanical Systems and Signal Processing，2007，21(5):2198-2211．

［19］Sherif B，Toshiyuki O，Shuichi M．Wavelet-based technique for structural damage detection ［J］．Mechanical Systems and Signal Processing，2010，17(5):473-494．

［20］Chen H P，Bicanic N．Assessment of damage in continuum structures based on incomplete modal information［J］．Computers ＆ Structures，2000，74(5):559-570．