Scheduling Problems on Parallel Identical Unbounded Batch Processing Machines

LIU Li-li,ZHANG Feng

(1.School of Science,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China; 2.Human Resources Department,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China)

Scheduling Problems on Parallel Identical Unbounded Batch Processing Machines

LIU Li-li1,ZHANG Feng2

(1.School of Science,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China; 2.Human Resources Department,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China)

The problem of scheduling jobs with dif f erent release dates or same release dates on parallel identical unbounded batch processing machines to minimize several scheduling criteria is considered.Pseudo-polynomial time dynamic programming algorithm,or fully polynomial time approximation scheme is developed for the scheduling problem under consideration,respectively.

scheduling;batch processing machine;release date

0 Introduction

We explore the problem of scheduling jobs with dif f erent release dates on parallel identical unbounded batch processing machines which is motivated by the burn-in operations in the f i nal testing stage of semiconductor manufacturing.This model can also be applied in the other manufacturing industries.A batch processing machine can process several jobs at the same time.The processing time of the batch is the longest processing time of the jobs in this batch.The jobs in the same batch start and complete at the same time.A batch cannot be interrupted during processing,new jobs cannot be added to the batch, either.

We describe the problem under study as follows.N jobs are processed on m parallel identical unbounded batch processing machines.Job Jj(j=1,···,n)has a release date rj,a processing time pjand a due date dj.The machine capacity is denoted as B.An unbounded batch processing machine can process up to n jobs at the same time,that is B≤n.In a feasible schedule,we use Cjdenote the completion time of job Jj.We consider criteria of minimizing the makespan Cmax,the maximum tardiness Tmaxand the number of tardy jobsUj.We use the three- fi eld notation of Graham et al.[1]to denote a scheduling problem,for example,Prepresents the problem of scheduling jobs with di ff erent release dates on parallel identical unbounded batch processing machines to minimize the makespan.

Pseudo-polynomial time algorithms and approximation algorithms are powerful approaches to deal with scheduling problems.An algorithm that runs in polynomial time under unary encoding scheme is called pseudo-polynomial time algorithm.A 1+ε approximation algorithm for a minimization problem with ε＞0 is a polynomial time algorithm that can produce for every instance a feasible schedule whose expected objective value is within a factor of 1+ε of the optimal value.A family of 1+ε approximation algorithms over all ε＞0 with polynomial running time in the problem input size is called a polynomialtime approximation scheme(PTAS for short).If the time complexity of a PTAS is polynomial in the problem input size and 1/ε,then it is called a fully polynomial-time approximation scheme(FPTAS for short)[2].

Brucker et al.[3]developed polynomial time algorithms for minimizing total weighted completion time, maximum lateness,and number of tardy jobs on an unbounded batch processing machine.They proved that minimizing total weighted number of tardy jobs and minimizing total weighted tardiness on an unbounded batch processing machine are ordinary NP-hard.Liu et al.[4]proved that minimizing total tardiness on an unbounded batch processing machine is ordinary NP-hard.Cheng et al.[5]proved that the problem with dif f erent release dates and deadlines on an unbounded batch processing machine is NP-hard even if the processing times and deadlines of the jobs are agreeable.Deng et al.[6]proved that scheduling jobs with dif f erent release dates on an unbounded batch processing machine to minimize total weighted completion time is ordinary NP-hard.Liu et al.[7]showed that scheduling jobs with dif f erent release dates and deadlines on parallel identical unbounded batch processing machines is strongly NP-hard,and a PTAS is presented for this problem.Liu et al.[8]showed that scheduling jobs with dif f erent release dates on a single unbounded batch processing machine to minimize the total completion time is NP-hard with respect to id-encoding and on parallel identical unbounded batch processing machines to minimize the total weighted completion time is strong NP-hard.Liu[9]presented a PTAS for the problem of scheduling jobs with dif f erent release dates on parallel identical unbounded batch processing machines to minimize total weighted completion time.Liu et al.[10]proved the problem of scheduling jobs with dif f erent release dates on parallel identical unbounded batch processing machines to minimize total completion time is strongly NP-hard.

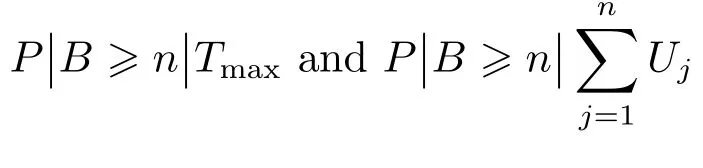
1 Scheduling problems with dif f erent release dates

We fi rst consider the problem of scheduling jobs with di ff erent fl release dat fles on parallel identical unbounded batch processing machines to minimize the makespan Pfl rj,B≥nlfCmax.The complexity of this problem remains open.We say that a schedule is in the batch-LPT order if for any two batches B1and B2in this schedule,batch B1is processed before batch B2and there does not exist two jobs Ji,Jjsuch that Jiin Bfl1,Jjin flB2and pi＜pj[2].It is easy to see that there exists an optimal schedule for problem Pfl rj,B≥nlfCmaxin which jobs are arranged in batch-LPT order on all the machines.

First order the jobs in increasing order of their processing times,we propose the following forward dynamic programming algorithm which runs in pseudo-polynomial time for the f i xed number of machines case.

Initial conditions:

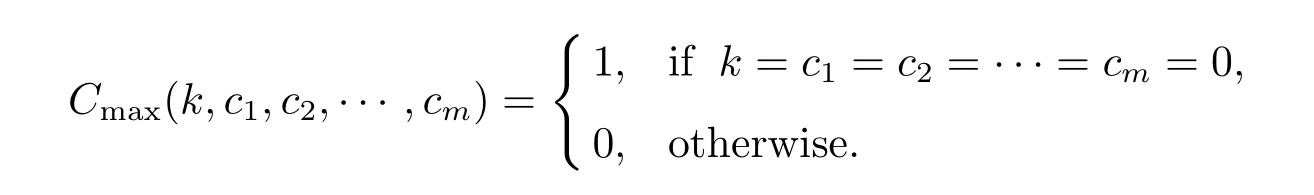
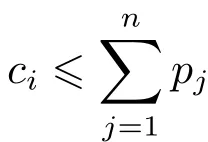
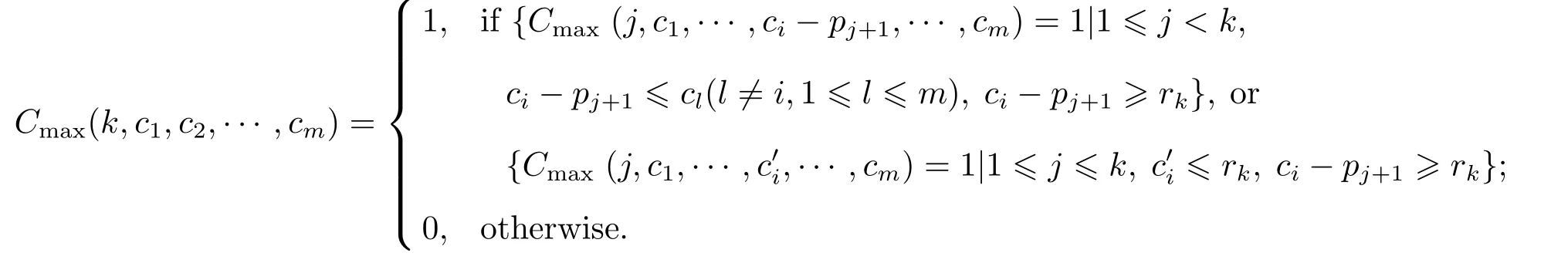
Function Cmax(k,c1,c2,···,cm)equals to 1 if the f i rst k jobs have been scheduled and the completion time of the last batch comprising jobs Jj+1,···,Jkon machine i is ci.The optimal value equals to min{ci}|Cmax(n,c1,c2,···,cm)=1,0≤and the time complexity of this algorithm isHence we have the following theorem.

Theorem 1Problem P|rj,B≥n|Cmaxcan be solved in pseudo-polynomial time for the case where there is a f i xed number of machines.

Based on the above dynamic programming algorithm,we develop an FPTAS for problem P|rj,B≥n|Cmaxwith a f i xed number of machines,which is denoted by Algorithm A.

Algorithm A

Step 1.For any given instance and any given ε＞0,let M=εpmax/n.

Step 2.Scale and round down the processing times of the original instance with=¥pj/Mƒ.

Step 3.Apply the dynamic programming algorithm provided above to the scaled and rounded down instance in Step 2 and return the resulting schedule to the original instance.

Theorem 2Algorithm A is an FPTAS for the problem P|rj,B≥n|Cmaxwith a f i xed number of machines.

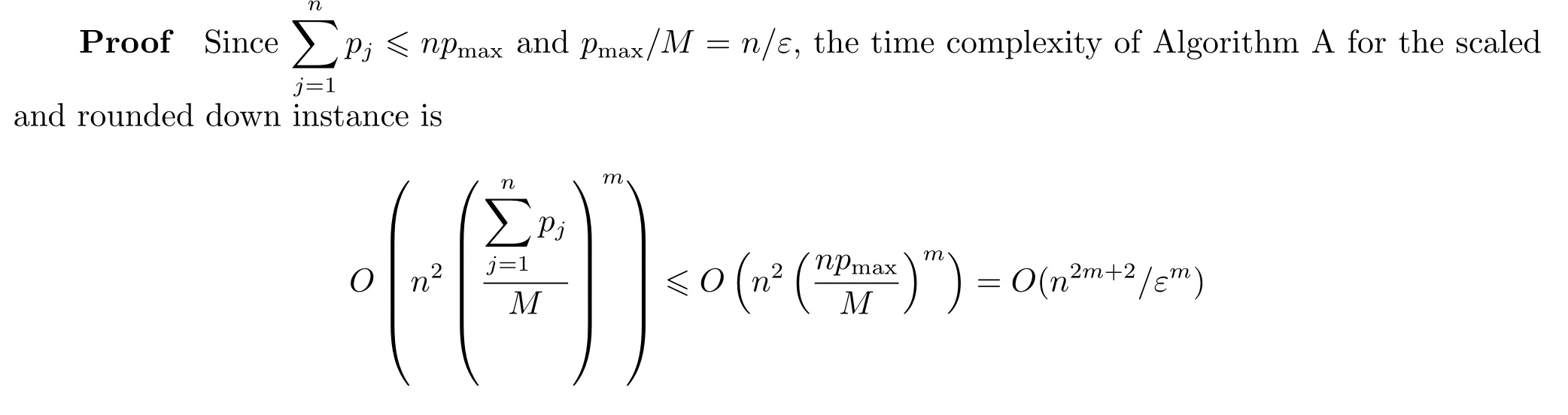
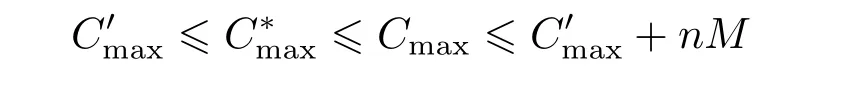
Therefore,Cmax−≤nM.Since M=εpmax/n and pmax≤we can obtain

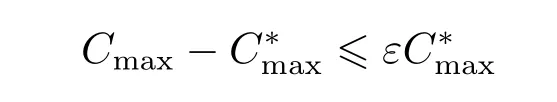
The time complexity of Algorithm A is polynomial in the instance size n and 1/ε when the number of machines are f i xed for any given ε＞0,therefore it is a fully polynomial time approximation scheme.

2 Scheduling problems with same release dates

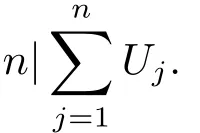
For problem P|B≥n|Tmax,we present the following forward dynamic programming algorithm.

Initial conditions:

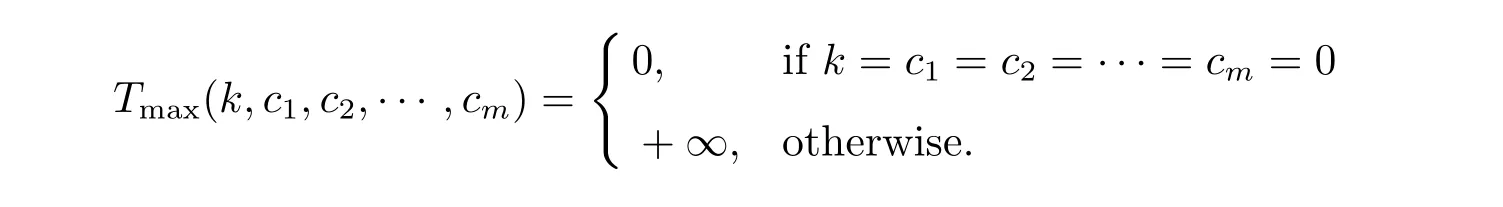
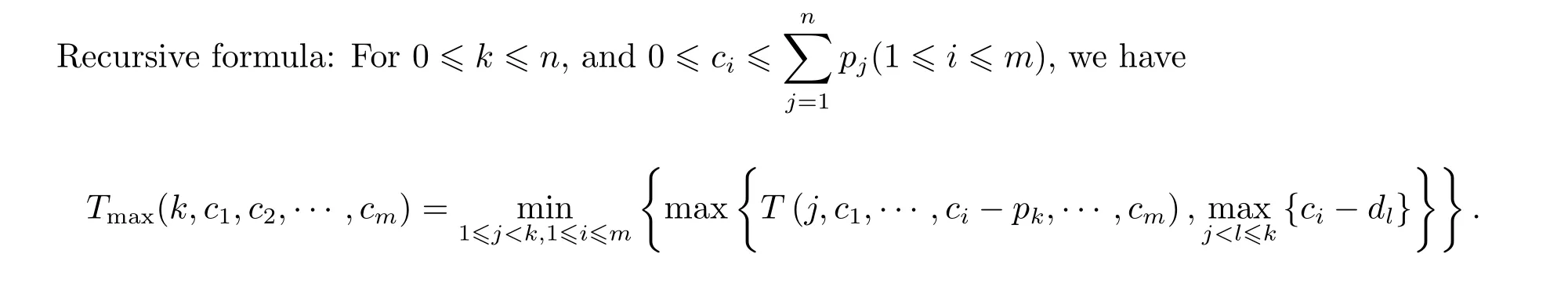
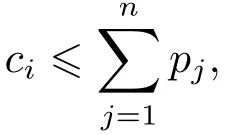
Initial conditions:

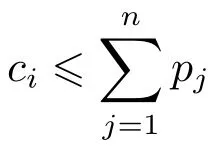
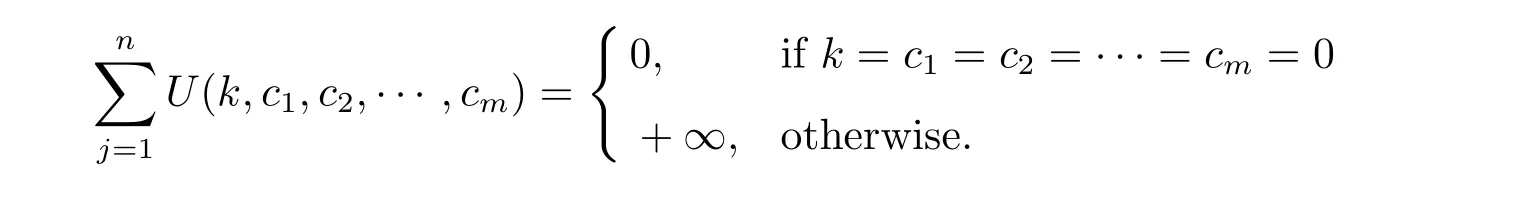
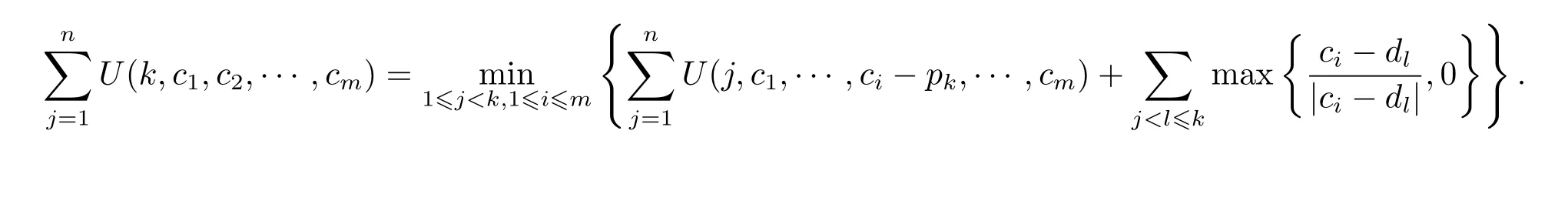
3 Conclusion

In this paper we study several scheduling problems with dif f erent or same release dates on parallel identical unbounded batch processing machines,pseudo-polynomial time dynamic programming algorithm or FPTAS is presented for the corresponding problem.

One of our future work is to investigate whether the above discussed problems are binary NP-hard or polynomially solvable for the f i xed number of machines case,and whether they are NP-hard or not for the general case.

[1]GRAHAM R L,LAWLER E L,LENSTRA J K,et al.Optimization and approximation in deterministic sequencing and scheduling:a survey[J].Annals of Discrete Mathematics,1979,5(2):287-326.

[2]LIU L L.Batch Scheduling Problem[M].Hong Kong,China:Hong Kong Polytechnic University,2007.

[3]BRUCKER P,GLADKY A,HOOGEVREEN H,et al.Scheduling a batching machine[J].Journal of Scheduling, 1998,1(1):31-54.

[4]LIU Z H,YUAN J J,CHENG T C E.On scheduling an unbounded batch machine[J].Operations Research Letters, 2003,31(1):42-48.

[5]CHENG T C E,LIU Z H,YU W C.Scheduling jobs with release dates and deadlines on a batch processing machine [J].IIE Transactions,2001,33(8):685-690.

[6]DENG X T,FENG H D,ZHANG P X,el al.Minimizing mean response time in batch processing system[J]. Algorithmica,2004,38(4):513-528.

[7]LIU L L,NG C T,CHENG T C E.Scheduling jobs with release dates on parallel batch processing machines[J]. Discrete Applied Mathematics,2009,157(8):1825-1830.

[8]LIU L L,NG C T,CHENG T C E.On scheduling unbounded batch processing machine(s)[J].Computers& Industrial Engineering,2010,58(4):814-817.

[9]刘丽丽.工件有到达时间的平行机分批排序问题的一个PTAS算法(英文)[J].科学技术与工程,2009,9(12):1623-1627.

[10]LIU L L,WANG,J B,ZHANG F.Scheduling jobs on parallel batch processing machines[C]//ISECS International Colloquium on Computing,Communication,Control,and Management,2009,1(1):78-81.

机器容量无限的同型机分批排序问题

刘丽丽1,张峰2
(1.上海第二工业大学理学院,上海201209;2.上海第二工业大学人事处,上海201209)

分别研究了最小化不同目标函数的工件有相同就绪时间和不同就绪时间的同型机分批排序问题,对于所研究的问题设计了伪多项式时间的动态规划算法或者完全多项式时间框架。

排序;分批加工机器;就绪时间

O22

A

1001-4543(2013)03-0197-05

2013-03-22;

2013-08-17

刘丽丽(1976–),女,山东滨州人,副教授,博士,主要研究方向为组合最优化,电子邮箱llliu@sspu.edu.cn。

上海市教委科研创新项目(No.12YZ178)资助