基于流固耦合的离心风机叶轮动力特性分析

吴正人， 王松岭， 戎 瑞， 孙 哲

（华北电力大学 电站设备状态监测与控制教育部重点实验室，保定 071003）

风机是工业生产部门的重要机械设备，其运行状况直接关系到工业系统的安全性.叶轮振动是风机的常见故障，引起振动的原因多样，如转子质量不平衡、转子不对中、转子周围的气流压力脉动等［1］.在设计和制造阶段，对风机进行静力分析时，通常只考虑风机的离心力，而忽略了风机的气动特性，尤其是气流压力脉动导致的叶轮动应力问题.实际运行中，在交变载荷作用下，叶轮有可能会出现结构的疲劳破坏问题［1-3］，造成安全隐患.

风机在工作过程中，叶轮内气体的非定常流动会对叶片施加一个非定常作用力，使叶片产生振动，而叶片的振动反过来又作用于流场，使流场的非定常程度发生变化，这类现象属于典型的气固耦合振动问题，需要考虑叶片的弹性变形与振动对流场的影响以及振荡流场的反作用，对该类问题的研究难度较大.

Kim对蒸汽压缩机叶轮叶片的疲劳问题进行了研究，发现叶片铸造过程中存在缺陷是导致叶片破坏的直接原因［4］.郭兴贵对600MW锅炉的离心式冷一次风机叶片的断裂进行了试验研究，结果表明：叶片进口端两侧的三角形工艺缺口结构导致明显的应力集中，是造成叶片断裂的主要因素，而高周低交变应力疲劳是叶片脆断失效的根本原因［5］.Ejaz对离心压缩机叶轮进行了研究，发现疲劳裂纹最初产生在有铸造缺陷叶片的根部，而高周疲劳最终导致叶片失效［6］.王春林研究了混流式核主泵内流体非定常压力脉动特性，并分析了影响脉动频率的主要因素［7］.Frantisek给出了一种预防旋转机械叶轮产生疲劳的方法［8］.毛军对大型轴流风机叶片的气动弹性进行了数值研究，发现叶片的气动弹性对叶片结构的强度有一定影响，在校核叶片强度时应加以考虑，否则容易高估叶片结构的安全性［9］.目前的研究主要集中在对叶片材料缺陷和加工制造等方面引起叶轮疲劳破坏的分析，有关由交变应力引起叶轮疲劳破坏的研究很少，且尚未见到有关离心风机方面的文献.

由于离心风机内部非定常流动的复杂性，采用理论分析或试验研究的方法很难获取足够精度的叶片表面载荷信息，而多物理场的数值模拟可以很好地解决这一问题.求解流固耦合问题一般有2种计算方法：强耦合法和弱耦合法.强耦合法物理概念清楚，主要用于流体－固体耦合场的理论分析，不适用于实际的工程应用.弱耦合法是在每一个时间步内分别对计算流体动力学方程和计算结构动力学方程进行求解，流场和结构场的计算结果通过搭建的中间数据交换平台彼此交换信息，从而实现2个物理场的耦合求解.此方法的优点在于求解过程中2个物理场相互独立，可以充分发挥各自领域的长处，计算结果也具有较高的精度.

笔者以电站常用的G4－73No.8D型离心风机为研究对象，采用弱耦合法对考虑流固耦合作用的叶轮进行强度分析，获得稳态流固耦合作用下叶轮的变形和应力变化情况，并对叶轮进行模态分析，从而得到叶轮的固有频率和振型.利用CFX对风机流场进行非定常数值模拟，获得叶轮周围的气流压力脉动情况，研究非定常气动力对叶轮振动特性的影响，为风机设计及安全运行提供理论依据.

1 计算模型

1.1 风机流场模型

1.1.1 风机模型和网格划分

采用Solid Works软件建立风机模型，在建模过程中对风机结构进行适当简化，未考虑风机集流器与叶轮间的泄漏损失.为了得到相对合理的网格数量，进行了网格无关性验证，最终确定了各个部分的网格数量，其中入口段20万、蜗壳80万、叶轮100万以及出口段20万，共计220万.风机网格划分结果见图1.

图1 风机网格划分结果Fig.1 Grid division of the fan

1.1.2 湍流模型和边界条件

湍流模型选择SST k－ω两方程湍流模型，SST k－ω湍流方程为

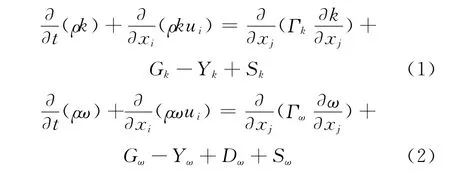
式中：Gk为湍动能；Gω是由ω方程产生的；Γk和Γω分别为k和ω的有效扩散项；Yk和Yω分别代表k和ω的发散项；Dω为正交发散项；Sk和Sω为用户自定义项.

环境压力为一个标准大气压，空气密度为1.225 kg／m3，计算中忽略重力对流场的影响.风机进口边界条件为速度进口，出口边界条件为压力出口，进、出口湍流强度和湍流长度尺度均依据经验公式计算确定.风机壁面均按光滑壁面处理，并采用无滑移壁面边界条件，壁面函数采用自动壁面函数.设定风机转速为1450r／min，设计工况下风机体积流量为6.318m3／s.

在定常数值模拟计算时，静止区域与旋转区域的交界面采用冻结转子（Frozen Rotor）模型，风机各个部分之间采用General Grid Interfaces（GGI）方法进行连接.在非定常数值模拟计算时，静止区域与旋转区域的交界面采用瞬态转子－静子（Transient Rotor－stator）模型，计算时间步长为1.149×10－4s，并选取3个流量（0.84、1.0和1.16倍设计流量）进行非定常计算.

1.2 叶轮结构模型

1.2.1 叶轮模型和网格划分

图2给出了叶轮和叶片的三维实体模型.叶片为翼型中空叶片，叶轮直径为80cm，前盘厚度为0.4cm，后盘厚度为0.5cm，叶片出口安装角为45°.叶轮材料为 Q235，其力学性能参数［10］见表1.采用四面体技术划分网格，并对局部区域进行加密，网格数量约为30万.

图2 叶轮和叶片的三维实体模型Fig.2 Three－dimensional model of the impeller and blade

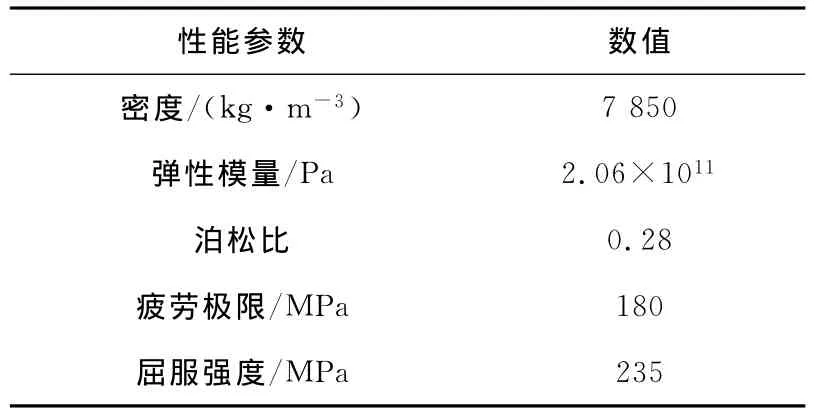
表1 叶轮材料的力学性能参数Tab.1 Mechanical properties of the impeller material

1.2.2 施加载荷

叶轮所受载荷包括惯性力和气动力，其中惯性力包括叶轮的重力和由于旋转引起的惯性离心力，气动力是风机内部流体所产生的作用在流固耦合界面（叶轮表面）上的力.对叶轮与轴的接触面进行全自由度约束，通过计算得到的流场，采用插值的方式使气动力作用于叶轮表面.

1.2.3 数学模型

进行静力分析时，方程如式（3）所示

进行模态分析时，假设叶轮结构为自由振动并且忽略阻尼的影响，方程如式（4）所示

式中：M为质量矩阵；K为刚度矩阵；F为作用在结构上的力；x为位移矢量；为加速度矢量.

由于在载荷作用下，结构的应力状态可能会影响自身的固有频率，分别在是否考虑预应力效应的情况下进行了计算.

采用Block Lanczos方法进行模态提取，该方法的优点是仅通过矩阵的相乘运算即可获得结构离散化模型较好的假设模态矩阵，它所张成的模态空间能有效地逼近结构离散化模型的低维模态空间，并且这种方法一般不会发生漏根现象.

2 计算结果与分析

2.1 定常流固耦合计算

2.1.1 流场结果与分析

图3给出了考虑流固耦合作用前后风机的性能曲线.由图3可知，模拟值与试验值比较接近，二者符合程度较好，说明模拟时边界条件的设置是合理的，并且全压模拟值基本上比试验值略大一些，可能是由于本文未考虑风机集流器与叶轮的泄露损失造成的，二者最大相对误差为1.9%.此外，双向流固耦合作用下的风机全压比单向流固耦合作用下的全压低1～2Pa，说明叶轮的变形对风机气动性能的影响很小，可以忽略.

“院长驾驶舱”是新名词，也是目前多家大型公立医院信息化运维能力的体现。各医院管理者力求通过这一手段，遍览医院管理和医疗业务数据，其中包括门诊量、住院量、门诊收入、住院收入、床位使用率、出院患者平均住院日、床位周转次数、药品库存金额、高值耗材库存金额、试剂库存金额等。

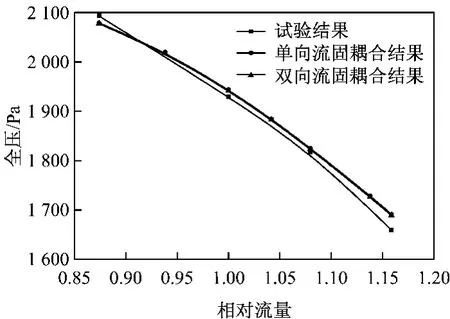
图3 考虑流固耦合作用前后风机的性能曲线Fig.3 Performance curves of the fan before and after the consideration of fluid－solid interaction

2.1.2 结构场结果与分析

首先在设计工况下对风机叶轮的变形和应力进行分析.图4给出了不同载荷工况下叶轮的总变形云图.由图4可知，不同载荷工况下叶轮总变形的变化趋势相同，最小总变形发生在轮毂区域，最大总变形发生在叶片吸力面的中间位置.此外，离心力对叶轮总变形的影响最大，重力对叶轮总变形有一定影响，使最大总变形量增加，增加幅度约为5.4%，气动力对叶轮总变形也有一定的影响，使最大总变形量减小，减小幅度约为2.5%.

图4 不同载荷工况下叶轮的总变形云图Fig.4 Contours of impeller total deformation under different load conditions

图5给出了不同载荷工况下叶轮的等效应力云图.由图5可知，不同载荷工况下叶轮的等效应力变化趋势相同，最小等效应力均发生在轮毂区域，最大等效应力均发生在叶轮前盘，随着载荷数量的增加，最大等效应力逐渐增大.此外，由图5还可以看出，与重力相比，气动力对叶轮等效应力的影响更大，使最大等效应力增大约3.6%，但叶轮的等效应力分布和大小主要还是由离心力决定的.

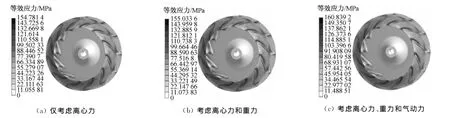
图5 不同载荷工况下叶轮的等效应力云图Fig.5 Contours of impeller equivalent stress under different load conditions

为了解在不同工况下风机叶轮的变形和等效应力变化情况，对其他几个工况下的叶轮变形和等效应力情况进行了研究.由于其他几个工况下叶轮的变形和等效应力分布与设计工况下相似，因此不再给出叶轮的总变形和等效应力云图.

图6和图7分别给出了不同工况下最大总变形量和最大等效应力的变化情况.由图6和图7可知，随着流量的逐渐增加，最大总变形量和最大等效应力都逐渐增大，但增大幅度很小，可以忽略不计.此外，叶轮的最大等效应力值为160.97MPa，而叶轮材料的屈服强度为235MPa，通过计算可知叶轮的安全系数为1.46，所以叶轮是偏于安全的.

图6 不同工况下最大总变形的变化情况Fig.6 Curves of maximum total deformation under different operation conditions

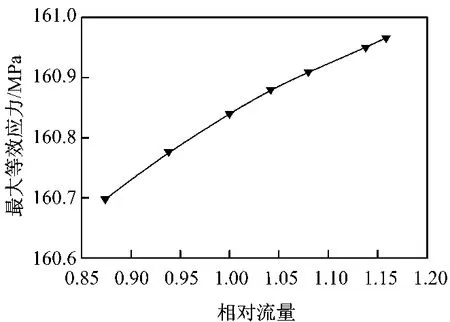
图7 不同工况下最大等效应力的变化情况Fig.7 Curves of maximum equivalent stress under different operation conditions

2.2 模态结果与分析

叶轮在正常工作状态下和静止状态下，分别考虑预应力效应时，叶轮固有频率的变化情况见表2.由表2可知，考虑预应力效应时叶轮各阶固有频率均有所提高，叶轮的固有频率在3种不同载荷工况下基本保持不变，因此由重力和气动力作用所产生的预应力对叶轮的固有频率基本没有影响，实际计算时可以将这2种力忽略不计，而只考虑离心力的作用.由于叶轮结构属于循环对称结构，因而叶轮结构的固有频率有重频现象.

图8给出了考虑预应力效应的叶轮固有频率与振型分布.由图8可知，叶轮共振时所产生的振动主要为扇形振动，其中第1和第2阶固有频率为重频，是具有1根节径的扇形振动；第3阶振型为伞形振动；第4和第5阶固有频率为重频，是具有2根节径的扇形振动，由于轮盖厚度相对较薄，导致轮盖刚度不足，发生较大变形；第6阶振型为伞形振动；第7和第8阶固有频率为重频，是具有1根节径的扇形振动；第9和第10阶固有频率为重频，是具有2根节径的扇形振动.

2.3 叶轮振动特性分析

2.3.1 非定常模拟结果与分析

叶轮振动可以通过两方面来影响流场：一是通过结构振动对流体边界进行影响；二是通过结构振动所激励的弹性波即声场对流场进行影响.由于叶轮变形很小、流体不可压缩，特征马赫数远小于1，因此叶轮振动对流场的影响基本可以忽略不计［12-13］，所以用非耦合的非定常流动代替耦合的非定常流动.

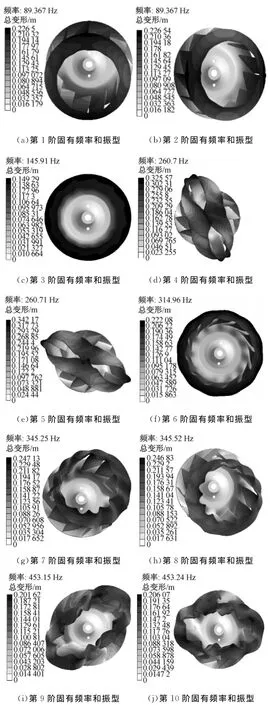
图8 考虑预应力效应的叶轮固有频率和振型分布Fig.8 Distribution of natural frequency and vibration mode of impeller considering the prestressing effect

通过监测叶轮中压力等物理参数随时间的变化规律可以获得气流的脉动频率.在叶轮出口处和某流道内布置监测点，监测点1～7所在平面为轮盖与轮盘的中间平面，监测点8和9分别靠近轮盖和轮盘侧，与监测点6的x、y坐标相同、z坐标不同，具体监测点位置见图9.

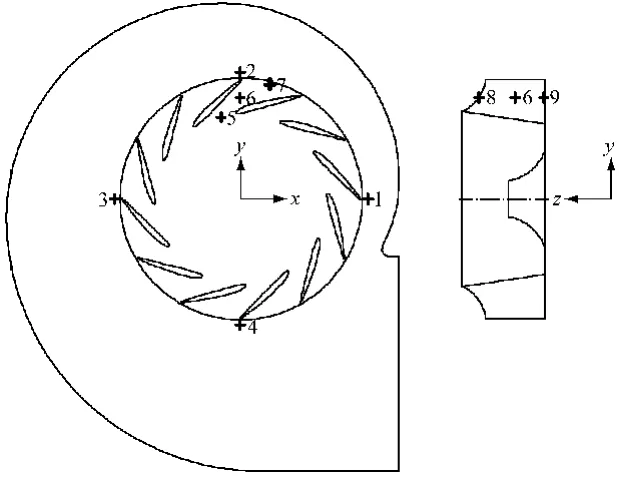
图9 监测点位置分布图Fig.9 Arrangement of monitoring points

图10给出了监测点2的静压随时间的变化.由图10可知，该点静压随时间的变化呈正弦曲线，在1个旋转周期内，静压曲线出现12个峰值，且分别对应于叶轮的12个叶片.以最佳效率点工况处流量QBEP为参照，比较不同流量下静压的波动规律可知，随着流量的逐渐增大，该点静压逐渐升高，且波动范围逐渐增大.

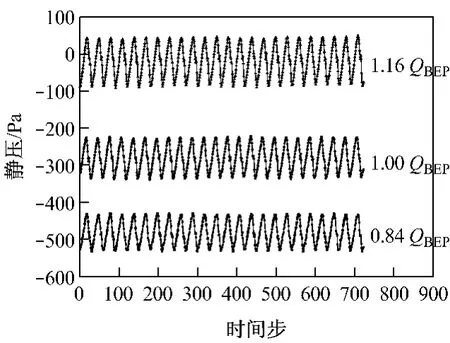
图10 监测点2的静压随时间的变化Fig.10 Curves of static pressure varying with time at monitoring point 2

对不同流量下采集到的点2的数据进行功率谱分析，结果示于图11.由图11可知，不同流量下气流压力脉动的主频不变，均为287Hz，且随着流量的增加，脉动强度逐渐增强.所研究叶轮的旋转速度为1450r／min，叶片数为12片，叶片通过频率的基频值为290Hz，与不同流量下气流压力脉动的主频基本相同，说明叶轮出口处的非定常扰动主要来源于叶轮的旋转.

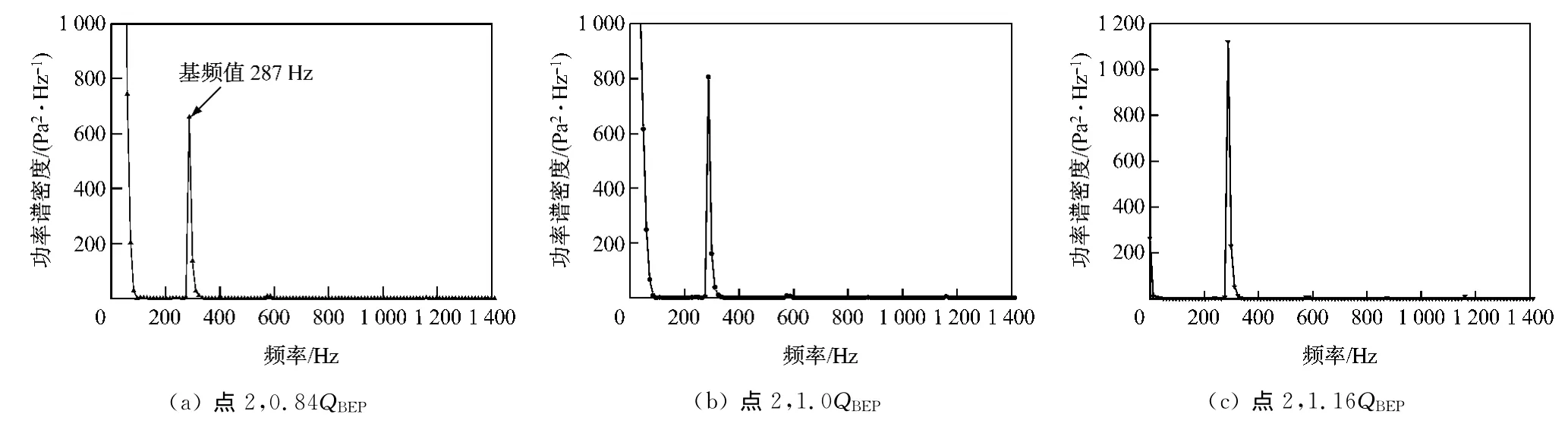
图11 监测点2的频谱图Fig.11 The spectrum chart at monitoring point 2

图12给出了不同监测点的频谱图.由图12可知，在叶轮流道内，不同监测点的气流主要脉动频率基本相同，仅存在脉动强度的差异，其中靠近轮盖侧点8的气流强度是中间位置点6气流强度的1.485倍，是靠近轮盘侧点9的1.494倍，而点5的气流强度是点6的1.72倍，是点7的55.1倍.比较图11和图12可知，在叶轮周围的气流脉动主频率基本相同，等于叶轮叶片的通过频率，且脉动强度沿流体流动方向逐渐减弱.

2.3.2 频率余量计算及振动分析

频率余量计算公式［14］为

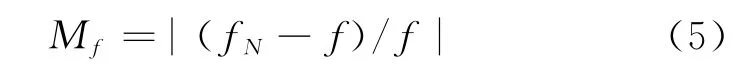
式中：fN为叶轮第N 阶固有频率；f为作用在叶轮表面非定常气动力的主频，f＝290Hz.为了避免共振破坏，一般要求频率余量大于20%［14-15］.

表3给出了计算得到的叶轮固有频率与非定常气动力主频率之间的频率余量.图13为考虑流固耦合作用时的叶轮总变形和等效应力云图.由表3可知，第4、第5和第6阶固有频率与气动力主频率之间的频率余量均小于20%，非定常气动力主频率落入第4到第6阶模态的局部共振区.其中，第6阶频率余量最小，因此其振幅放大因子最大.由图8（f）可以看出，叶轮第6阶振型表现为轮盖外缘附近区域的局部振动.因此，可以推断在非定常气动力的作用下，轮盖外缘附近区域将形成局部共振.由图13可知，在3种载荷共同作用下，叶轮轮盖外缘附近区域的变形量和等效应力都较小，且等效应力远小于叶轮材料的疲劳极限，所以该区域不会发生疲劳破坏.

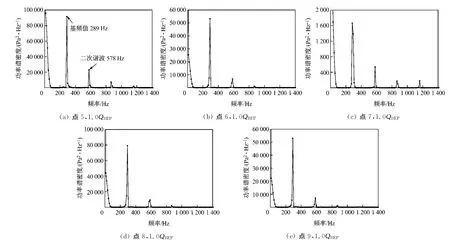
图12 不同监测点的频谱图Fig.12 Spectrum charts at different monitoring points

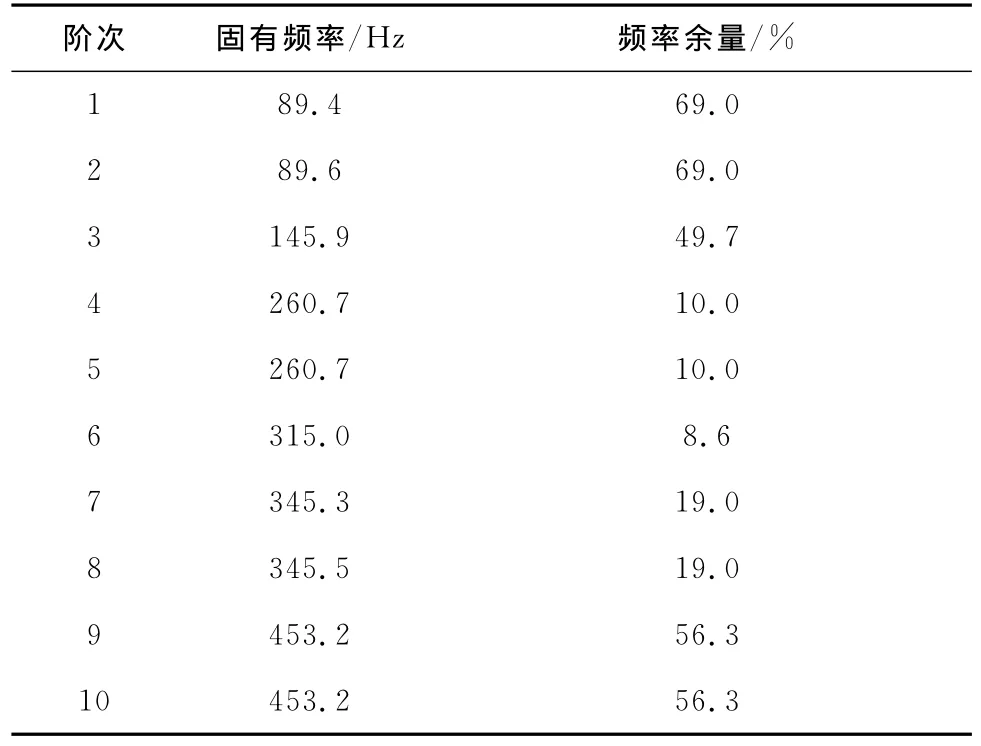
表3 叶轮固有频率与非定常气动力主频率之间的频率余量Tab.3 Frequency margin between natural frequency and main unsteady aerodynamic frequency of impeller

图13 考虑流固耦合作用的叶轮总变形和等效应力云图Fig.13 Contours of impeller total deformation and equivalent stress in consideration of fluid－solid interaction

由于第4和第5阶固有频率为重频，所以分析其中之一即可.由图8（d）可以看出，叶轮第4阶振型表现为轮盖内缘附近区域的局部振动.由图13可知，轮盖内缘附近区域的变形量和等效应力都较小，且等效应力远小于叶轮材料的疲劳极限，所以该区域也不会发生疲劳破坏.

3 结 论

（1）考虑流固耦合作用前、后风机气动性能基本不变，流固耦合作用可以忽略不计，但流固耦合作用对叶轮的变形和应力大小有一定的影响，其中使叶轮最大总变形量减小2.5%，最大等效应力增大3.6%.

（2）预应力效应会使叶轮的固有频率有所提高，但不同阶次固有频率提高的幅度不同.在叶轮所受的3种载荷中，离心力对固有频率的提高起决定作用，其余2种载荷的影响可以忽略不计.

（3）叶轮周围的非定常气动力主要脉动频率等于叶轮叶片的通过频率，说明叶轮周围的非定常扰动主要来源于叶轮的旋转，且气流脉动强度沿流体流动方向逐渐减弱.

（4）叶轮固有频率部分落入局部共振区域，但由于该区域的等效应力远小于叶轮材料的疲劳极限，因此不会发生叶轮的疲劳破坏.

［1］刘家钰.电站风机改造与可靠性分析［M］.北京：中国电力出版社，2002：127－130.

［2］李松涛，许庆余.离心式叶轮流体激振响应及动态疲劳的研究［J］.应用力学学报，2007，24（3）：353－358.LI Songtao，XU Qingyu.Fluid induced vibration and dynamic fatigue in ceutrifugal impeller［J］.Chinese Journal of Applied Mechanics，2007，24（3）：353－358.

［3］BOURGEOIS H，PHILLIPS D E.Cause and cost［J］.Hydrocarbon Engineering，2003，8（5）：61－63.

［4］KIM T G，LEE H C.Failure analysis of MVR impeller blade［J］.Engineering Failure Analysis，2003，17（6）：307－315.

［5］郭兴贵，刘峰，李霞.2023t／h锅炉一次风机叶片断裂的分析与研究［J］.华北电力技术，2005（8）：8－13.GUO Xinggui，LIU Feng，LI Xia.Analysis and research on blade frature of primary fan for 2023t／h boiler［J］.North China Electric Power，2005（8）：8－13.

［6］EJAZ N，SALAM I，TAUQIR A.Fatigue failure of a centrifugal compressor［J］.Engineering Failure A－nalysis，2007，14（7）：1313－1321.

［7］王春林，易同祥，吴志旺，等.混流式核主泵非定常流场的压力脉动特性分析［J］.动力工程，2009，29（11）：1036－1040.WANG Chunlin，YI Tongxiang，WU Zhiwang，et al.Analysis on pressure fluctuations of unsteady flow field in mixed－flow main coolant pump［J］.Journal of Power Engineering，2009，29（11）：1036－1040.

［8］EISINGER F L.Acoustic fatigue of impellers of rotating machinery［J］.Journal of Pressure Vessel Technology，2002，124（2）：154－160.

［9］毛军，杨立国，郗艳红.大型轴流风机叶片的气动弹性数值分析研究［J］.机械工程学报，2009，45（11）：133－139.MAO Jun，YANG Liguo，XI Yanhong.Numeric analysis of on the pneumatic elasticity of large axialflow fan blade［J］.Journal of Mechanical Engineering，2009，45（11）：133－139.

［10］马安禧.材料力学［M］.北京：高等教育出版社，1979.

［11］王毅.大流量离心压缩机首级叶轮流固耦合数值模拟［D］.大连：大连理工大学动力机械及工程学院，2010.

［12］JIANG YY，YOSHIMURA S，IMAI R，et al.Quantitative evaluation of flow－induced structural vibration and noise in turbomachinery by full－scale weakly coupled simulation［J］.Journal of Fluids and Structures，2007，23（4）：531－544.

［13］蔡建程，祁大同，卢傅安.离心风机蜗壳振动辐射噪声的数值预测［J］.应用力学学报，2009，26（1）：115－119.CAI Jiancheng，QI Datong，LU Fuan.Prediction of noise radiated by the vibrating volute structure of centrifugal fan［J］.Chinese Journal of Applied Mechanics，2009，26（1）：115－119.

［14］毛义军，祁大同，许庆余.离心压缩机叶轮叶片疲劳断裂故障的数值分析［J］.西安交通大学报，2008，42（11）：1336－1339.MAO Yijun，QI Datong，XU Qingyu.Numerical study on high cycle fatigue failure of a centrifugal compressor impeller blades［J］.Journal of Xi'an Jiaotong University，2008，42（11）：1336－1339.

［15］邱凯.离心压缩机叶轮三维有限元强度与振动分析［D］.西安：西安交通大学能源与动力工程学院，1999.