BP神经元网络在凹版印刷机张力控制应用研究

赵宇峰

（广州市高级技工学校，广东广州510425）

0 引言

为了实现凹版印刷机的印刷工作，料带在进入色组印刷装置之前必须保持料面平整、适度绷紧，就是要保持一定的走纸张力。料卷在输送料带的过程中，使料带处于拉紧状态的力称为“张力”。

料带如果在印刷过程中处于毫无约束的自由状态，那料带就不能完成印刷工作。 同时，凹版印刷机的图像转移状态与料带的张力大小有直接关系。所以在印刷过程中，需要对料带施加一定的力量拉紧，才能够有效地控制它伸缩和运动。 由于套印的需要，在印刷过程中料带的张力需要恒定不变和大小适当。 如果张力大小不合适，就会造成纸带飘移、起皱裕、破口或撕裂、套印不准、天头、地脚位置不准等一系列工艺故障，从而造成废品，影响生产质量。 但是如果料带带张力过大，又会造成印刷网点会产生变形，料带带在纵向打皱、甚至发生横向断裂等印刷故障，影响印刷生产。因此凹版印刷机在印刷过程中，必须维持料带张力在一定范围内，以便控制料带的运动，保证印刷质量稳定。

长期以来在凹版印刷机的张力控制的调节手段是调整放卷辊与收卷辊的相对转速，控制器多使用PID 或者模糊PID 控制器。 在实际的运行中，这种控制组合有结构简单，维护容易的优势，但是实际控制效果较差。 特别是在压印色组之间的张力控制基本无法实现，严重制约了凹版印刷机印刷质量的提高。 因为在料带的运行过程中，有印前处理、多色组套印、印后处理、收卷/分切等环节，调节过程中，压印滚筒并未参与调节，而在相邻的压印滚筒之间，张力的变化更为复杂。使用传统的PID 或模糊PID，不能实现多输入、多输出的系统调节，本文针对这一情况，提出BP 神经元网络的张力控制方法。

1 张力控制方法

在凹版印刷机中，纸带的张力由于压印机组的间隔，每段都不同。凹印机生产过程如下：纸料从放卷辊开出，经过张力调节后到达放卷牵引辊，这一段称为放卷段。 放卷段的执行机构是力矩电机及其驱动装置。 纸料从放卷牵引辊出来到凹印牵引辊之间为凹印段。

放卷辊与第一色组之间的张力，是由放卷牵引辊角速度与放卷辊角速度之间的速度差得到的。同时由于放卷的料带随着印刷进行会不断消耗，导致放卷辊的半径不断缩小。为了维持张力稳定，放卷辊的角速度将随着辊径变小而不断增大，但是为了维持纸带张力稳定，放卷辊制动的力矩应随管径增大。在相邻两色组之间的纸带张力则是由于相邻压印辊之间的速度差决定。 由于压印滚筒的辊径不会大幅度变化，所以通过调节压印辊之间的相对速度，能够有效调节该段的纸带张力。 纸带张力的计算方法如下：

根据胡可定律纸带受到的拉力是由于纸带被拉伸变形所产生,得到：

式中，L0——相邻两辊之间被拉伸的纸料的长度；L——相邻两辊之间被拉伸后纸料的长度；ε——形变率；E——弹性模量；A——纸带的横截面积放卷牵引辊角速度ω1，放卷辊角速度ω2，辊径为R1，R2，得到：

将（2）带入式（1）中，得：

2 凹印机生产线的张力数学模型方框图

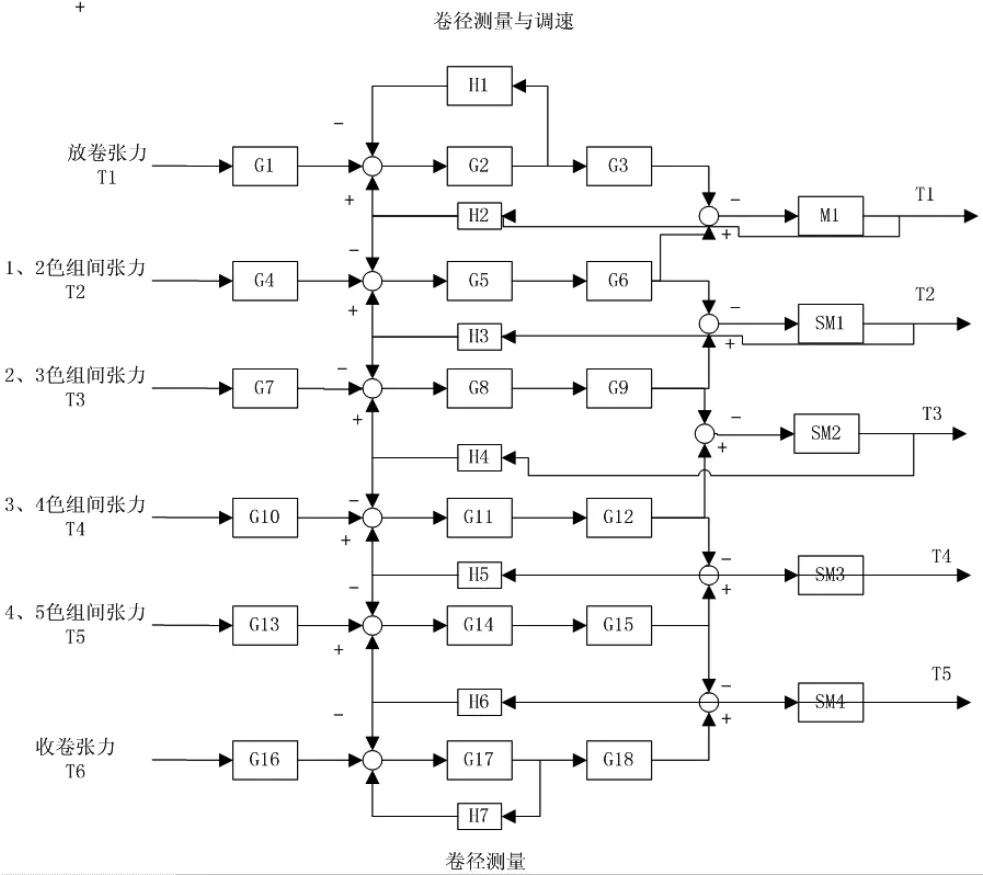
图1 凹版印刷机张力模型方框图

基于以上分析，可以得到凹印机生产线数学模型的方框图，如图1 所示。图中输入量T1-T6 为各段张力，通过张力传感器采集、变送获得电信号，并根据设定的张力比较计算各部分的张力偏差。 偏差信号与相邻滚筒的转矩反馈进行叠加，通过控制器对相应的上下辊筒进行速度调节，达到调节的目的。其中由于放卷辊、收卷辊的辊径会随着时间变化而变小、变大，因此建立内环。从凹印机生产线的方框图可以得出如下结论：

1）非线性和时变性。随着印刷过程的进行，料辊的半径不断减小，料卷质量不断变小，从而使得放卷辊的转动惯量不断变小，并且从印刷开始到结束，放料辊的模型变化很大，往往有十倍甚至几十倍的变化。

2）多干扰。料带的张力系统最主要的干扰来自料带线速度变化的干扰，如突然的加速、减速，启动和停止阶段；以及印刷过程中，相邻两色组间压印滚筒的不同步造成的拉伸或压缩效应；另外，就是印刷机械故障造成的干扰，如卷筒圆跳动，料辊质量分布偏心等，都会影响张力。

3）多输入多输出。凹印机系统是一个多电机同步协调动作的分段式张力控制系统，电机相对转速的变化将直接影响相应相邻两段料带段张力的大小。

因此，凹印机料带的张力系统属于时变，非线性和带干扰的多输入多输出系统。 对于该系统如果应用传统控制模式，很难要达到高精度的控制要求。

3 BP 神经网络控制器的设计

3.1 输入层的神经元节点数

凹版印刷机控制系统中， 整个料带的运行被分成了若干个区间，如从放卷辊到印前处理单元，印前处理单元到色组1，色组1 与色组2之间等等。 要使某段料带的张力保持在一定范围内，就要考虑印刷机系统运行的过程中能够影响到该段料带张力变化的因素。寻找到的这些影响张力变的因素的样本矢量数将用于BP 神经网络训练，也就是输入层的神经元节点数。

在凹印机放卷段，选择变频电机作为执行机构。根据分析，寻找到能够影响张力的输入因素有纸料的实时半径凡R0、转动惯量J0、放卷辊的线速度V0、 放卷牵引辊线速度V1以及实时纸料张力T0一共5个，因此输入层神经元节点数为5 个。 纸料的实时半径R0和转动惯量J0是神经元相关节点；随着印刷的进行，纸料不断消耗，料卷的半径在逐渐减小，随着料卷直径变化，料卷的转动惯量J0也会逐渐变小。另外料带的前后辊的线速度V0和V1也是神经网络的输入节点。

凹印机的色组印刷环节， 使用伺服电机驱动压印与印刷滚筒，在色组之间产生张力的主要方式是前后两色组之滚筒的相对速度。因此凹印段前色组前辊线速度、后辊线速度和实时纸料张力是神经元网络的机电，因此该段的节点数为3 个。

3.2 隐含层的神经元节点数

神经网络中的隐含层节点能把混杂于输入信号中相互独立的基本信号分离出来再组合出新的向量，即输出向量，以实现网络由输入到输出的映射。在凹版印刷的张力控制系统设计中，根据经验发现：隐含层节点的数目， 应该取输入层节点数和输出层节点数之间的数值；当隐含层节点数靠近输入节点数时，网络的收敛速度较快。根据经验，使用神经网络隐含层节点数的经验计算公式来确定张力控制系统隐含层节点数：

式中，n——输入层节点数；

m——输出层节点数；

n1——隐含层节点数。

由公式计算出放卷段的神经网络隐含层的节点数为9 个，凹印段神经网络隐含层的节点数为6 个。

3.3 输出层的神经元节点数K

放卷段使用的执行机构是变频电机，凹印段与分切段使用的执行机构是伺服电机，两者都可以使用模拟量电压控制。因此，神经网络的输出层神经元节点分别为变频电机和伺服电机的模拟量电压值u。 输出层的神经元节点数为1 个。

4 BP 算法学习步骤

BP 网络的训练过程如下： 正向传播是输入信号从输入层经隐含层传向输出层， 若得输出层得到了期望的输出， 则学习方法结束；否则，转至反向传播。

4.1 BP 神经网络的前向计算

设有N 个训练样本， 若用其中的某一训练样本p 的输入Xp和输出拟{dpk}对网络进行训练，则隐含层的第i 个神经元输入可写成：

隐层神经元的输出x′j采用S 函数激发xj，得到：

则

输出层神经元的输出为：

在神经网络的正常工作期间， 上面的过程即完成了一次前向计算，而若是在学习阶段，则要将输出值与样本输出值之差回送，以调整加权系数。

4.2 BP 神经网络的误差反向传播和加权系数的调整

在前向计算中，若ok与样本的输出dk不一致，就要将其误差信号从输出端反向传播回来，并在传播过程中对加权系数不断修正，使输出层神经元上得到所需要的期望输出dk为止。 对样本p 完成网络加权系数的调整后，再送入另一个样本进行学习,直到完成N 个样本的训练为止[4]。

为了对加权系数进行调整，对每一个样本p，引入二次型误差函数

则系统的平均误差函数为：

学习调整加权系数，即可按使误差函数Ep减少最快的方向调整，也可按使误差函数E 减少最快的方向调整， 直至获得加权系数集为止。 下面以按误差函数Ep减少最快的方向调整为例，也就是使加权系数按误差函数E，的负梯度方向调整，使网络逐渐收敛。

反向传播要采用梯度下降法，调整各层间的权值，输出层及隐层的连接权值wjl学习算法为：

式中，η 为学习速率，η∈[0，1]。 k+1 时刻网络的权值为

隐层及输入层连接权值wij学习算法为：

式中，

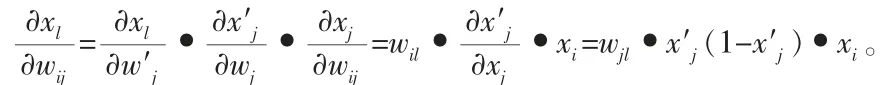
t+1 时刻网络权值为

BP 神经网络加权系数的学习计算步骤：1）用较小的随机数为BP神经网络的所有加权系数设置初值；2）提供训练集：给定输入向量X＝（x1，x2，…，xM）和期望的目标输出向量D ＝（d1，d2，…，dL），令n=1；3）按前向计算公式（4）-（7）计算隐含层和输出层各神经元的输出。 4）按式（9）计算目标值与实际输出的偏差函数Ep；5）按式（11）计算输出层加权系数的调整量Δwjl，并修正加权系数；6）按式（13）计算隐含层加权系数的调整量Δwij，并修正加权系数；7）n=n+1，返回到3，直到Ep进入事先设定的范围为止。

5 小结

本文提出使用BP 神经网络对凹版印刷机进行张力控制。 从而可以实现凹版印刷机的主要滚筒参与张力调节，能够调节每一段料带的张力和整个工作料带的张力，提高凹版印刷机的工作稳定性，提高产品质量。在实践应用后，与传统PID 控制方式相比，在并未增加太多硬件成本的条件下，获得了远远优于传统控制方式的效果。 有效的提高了凹版印刷机的性能和系统的抗扰动能力，该方法是行之有效的。

［1］孙玉秋.印刷过程自动化[M].印刷工业出版社.

［2］广东省软包装行业协会.广东省软包装印刷设备制造产业技术路线图[R].科学出版社.

［3］KazuyaA.,Kauhiroy.,TakashiK.Hot Strip Mill Tension-looper Control Based on Deeentralization and Coordination[J].Control Engineering Practiee,2000,8:337-344.

［4］Lightbody L,Iwin GW.Direet Neural Model Referenee Adaptive Control[J].IEEE Proc.Pt.D.Control Theory and pplieation,1995,142(1):31-43.

［5］SunF C,Sun Z Q.Stable neural network-based adaptive control of robot arms using neural networks[J].Journal of Intelligent and Robotic Systems,1998,20(2):1-22.

［6］孙宇新,刘贤兴.神经元控制器在数字调速系统中的实现和应用[J].电工技术学报,2005,20(3):3,85-89.