几何模型在TRT行程匹配中的应用

张春娟

（陕西鼓风机（集团）有限公司，西安 710611）

1 引言

陕鼓生产制造的能量回收透平发电装置（简称：TRT），是一种将高炉炉顶煤气具有的压力能和热能，通过膨胀作功转化为机械能，驱动发电机发电或驱动其它设备进行能量回收的一种装置。第一级静叶为全静叶可调的TRT，静叶角度的开度大小是由动力油站提供动力的伺服作动器来控制完成的，伺服作动器能否准确地调整控制TRT的静叶角度，是满足用户对风机性能要求的关键点，这也是TRT 装配工序的技术关键。

2 结构介绍

本文介绍的TRT 结构特点为伺服作动器驱动、一级静叶可调；可调的静叶通过曲柄滑块机构、摇柄机构和导向圈体（上下半水平剖分件）与伺服作动器连接，从而控制静叶角度的开度，具体见图1所示。导向圈体与摇柄机构组成导向机构，导向机构与安装在机壳上的伺服作动器连接在一起，伺服作动器是由动力油站提供的12MPa的动力油控制作直线往复运动，从而带动导向机构作小行程的圆周往复运动。曲柄滑块机构因导向圈体运动而不停转动，从而带动静叶作往复旋转运动，不断满足工况调整需要。从而可以看出：静叶角度的准确控制，取决于各个机构的匹配，如何有效匹配就成为TRT的装配难点，也是风机运行性能好坏的决定因素。

图1

3 存在问题

在TRT的装配中，我们在静叶角度的最小角的状态下，以导向机构的下半件为基准进行机构的初始匹配，最终导向机构上、下半扣合，再通过微量调整伺服作动器来完成机构的精确匹配。在导向机构图中给出伺服作动器的总行程，第一级静叶角度的最大角、中间角、最小角；以上参数对技术工人的操作来说，没有可操作性，因此转换以上参数，找到便于技术工人操作的参数，是我们急需解决的问题。

4 解决办法

4.1 建立几何模型

为了解决此问题，我们对相关参数之间的关联进行了分析。两大机构(曲柄滑块机构、导向机构)的相互配合实现了对静叶角度的控制，这需要找出整个驱动机构中的关键件，通过对导向机构图纸的分析，找出导向圈体是两大机构的共同载体。从图1 可以看出：曲柄滑块机构中的滑块安装在导向圈体内孔槽内，摇柄机构中的座架安装在导向圈体外圆上有一定角度的小平面上，因此导向圈体是我们解决问题的关键件；分析导向圈体在整个TRT 运转过程中的运动特性，成为解决此问题的关键点。

通过长期的工作经验总结，我们采用建立几何模型的办法有效解决了此问题，即将导向圈体的运动过程假定为匀速运动，当静叶角度在最大角、中间角、最小角的三种状态下，导向圈体运动到此三种位置的状态下进行几何模型的建立，结合图纸给出的已知条件：伺服作动器的总行程，第一级静叶角度的最大角、中间角、最小角和导向圈体的几何尺寸，建立如图2的几何模型，通过相似三角形的特性，将以上参数转化为式（1）和式（2），就可以计算出导向圈体外圆在第一级静叶角度从最大角旋转到中间角，或从中间角旋转到最小角时的运动变量值，此运动变量值便于技术工人的操作，从而解决了TRT 行程匹配中的操作难题。

其中：

L 为伺服作动器总行程；β1为第一级静叶角度的最大角；β2为第一级静叶角度的中间角；β3为第一级静叶角度的最小角；A、B 值可从导向机构图中查到。

从式（1）、式（2）可以计算出X1、X2值，即可知道第一级静叶角度在最大角、中间角、最小角的状态下导向圈体运动的相对位置。操作人员根据X1、X2值，以下半导向圈体中分面部位为基准，确定导向圈体在静叶角度极限位置时的变化量为X1、X2值，X1是静叶角度关到最小时的量，X2是静叶角度开到最大时的量。以上过程为设计要求值的相关计算过程，实际的匹配操作只须将导向圈体运动到X1或X2值位置，再将TRT的一级静叶角度确定为最小角或最大角，在此时将各个机构的相互位置确定，就完成行程的初始匹配。操作过程简单、直观、可行。

4.2 几何模型的应用（以某TRT 产品为例）

已知数据：第一级静叶角度的最大角β1=60°,中间角β2＝45°，最小角β3=20°，伺服作动器总行程 L=120mm；A=830mm，B=1020mm；按照图2 几何模型建立图3的简单几何模型图。利用以上数学公式计算:

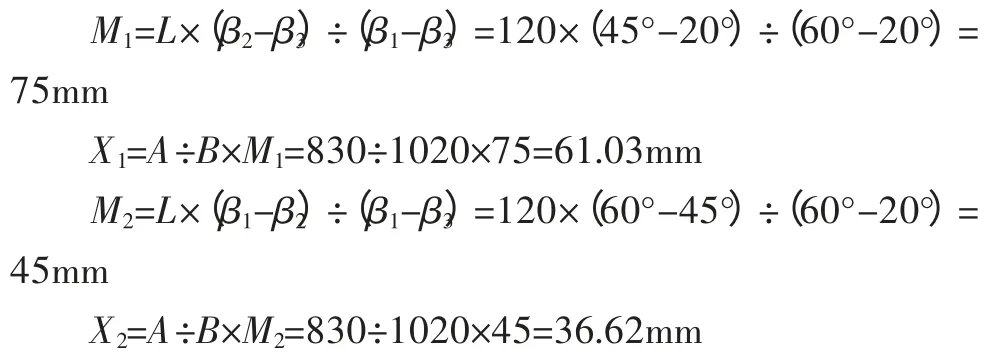
通过计算得出X1=61.03mm、X2=36.62mm，即可知道第一级静叶角度从中间角关到最小角时导向圈体运动值为61.03mm；第一级静叶角度从最大角关到中间角时导向圈体运动值为36.62mm。将导向圈体向关的方向运动61.03mm，第一级静叶角度定为20°，将导向圈体向开的方向运动36.62mm，第一级静叶角度定为60°，即完成行程匹配操作。

5 结论

在TRT 产品的行程匹配过程中，工程技术人员通过建立几何模型，并利用公式可快速计算出X1、X2值，技术工人依据X1、X2值即可完成行程的初始匹配，最终在检测静叶角度时微量调整伺服作动器来达到最佳匹配效果。通过在20 多台产品中应用此建立几何模型的方法，解决了TRT的行程匹配问题，均能满足图纸的精度要求。从而可以看出，在工程技术领域中建立几何模型的方法能解决实际生产技术难题，是一种有效可行的方法。

图3