基于模型的故障诊断专家系统测点优选策略

潘宇雄 李清东 任 章

(北京航空航天大学飞行器控制技术一体化技术国防科技重点实验室，北京 100191)

较为完善的基于模型的故障诊断方法是由de Kleer等［1］于1987年提出的，主要包括冲突识别和候选产生2个部分.在冲突识别方法中，de Kleer提出了“冲突集”的概念，也就是说当系统有故障时可以利用某些算法得到系统中所有的极小冲突集作为诊断的基础集合.然后采用候选产生方法，利用极小冲突集计算出作为候选诊断集的极小碰集.

利用极小冲突集计算出作为候选诊断集的极小碰集.在基于模型的故障诊断中，最早计算碰集的方法是由著名人工智能专家Reiter在1987年提出的采用HS－Tree求解碰集的方法［2］.至今已对碰集的计算方法进行了许多研究和改进，如HSDAG［3］，SE－TREE［4］，布尔代数方法等［5］，这些方法的最终目的都是要完备地、快速地求出所有极小碰集(即极小诊断).当待诊断系统的测点有限时，将产生极小诊断的组合爆炸问题［6］.如此计算出来的极小诊断，对于系统最终的故障定位作用不大.因此，针对这种情况，本文提出了一种基于测点优选和新增观测信息的减少极小诊断的新方法.通过观测信息的不断增加，极小诊断将逐渐减小;当观测信息足够多时，将会得到唯一极小诊断.

1 预备知识

定义1(系统) 一个系统定义为一个三元组(SD，COMPS，OBS)，其中，SD 为系统描述，是一阶谓词的集合;COMPS为系统组成部件的集合，是一个有限的常量集;OBS为观测集，是一阶谓词的有限集.以下使用一元谓词AB(·)表示“abnormal”，AB(c)为真当且仅当 c反常，其中 c∈COMPS.

定义2(冲突集) 系统的冲突集是一个集合{c1，c2，…，ck}⊆COMPS，满足下述条件:SD∪OBS∪{﹁ AB(c1)，﹁ AB(c2)，…，﹁ AB(ck)}是不一致的.如果称某冲突集为极小冲突集，当且仅当该冲突集的任意真子集都不是冲突集［2］.

定义3(极小依赖集) 称集合{d1，d2，…，dn}⊆COMPS为极小依赖集，若满足:﹁AB(d1)∧…∧﹁ AB(di－1)∧﹁AB(di+1)…∧﹁AB(dn)┝﹁AB(di).

命题1 若C={c1，…，cn}为一极小冲突集，D={d1，d2，…，dm}为一极小依赖集，则集合( C∪D)－ ( C∩D)(即C与D的对称差)也是一个极小冲突集.

定义4(P－S子系统) 在一个系统中，由一个元件及其所有的与此元件输入直接相连的元件构成一个P－S(Parents－Son)子系统，也称为以此元件为输出的P－S子系统.在以X为输出的P－S子系统中，如果X对它的输入元件不敏感，称为含有故障掩盖的P－S子系统.

命题2 一个非故障掩盖的P－S子系统要么是一个极小冲突集，否则为一个极小依赖集.

定义5(碰集) 设F是集合簇，称H为F的一个碰集，如果H满足

2)对每个S∈F，都有H∩S≠Ø.

如果称某碰集为极小碰集，当且仅当该碰集的任意真子集都不是碰集.

2 求解碰集

求解极小碰集的过程也就是求解极小诊断的过程，其主要流程如下［4］:

步骤1 首先，根据模型系统的参数变量极其连接关系建立元件矩阵、元件参数矩阵和参数变量矩阵［7］，然后利用这3个矩阵根据每个元件的行为模式可以推理出系统的预测输出值与实际输出值是否一致.如果不一致，则相应输出所对应的P－S子系统所包含的元件集合为一个极小冲突集，否则为一个极小依赖集.对于m+n个输出的系统，可以得出极小冲突集的集合簇P={p0，p1，…，pn}和极小依赖集的集合簇 N={n0，n1，…，nm}(m，n 均为正整数).

步骤2 判断N是否为空，如果不是，则将N中每一个集合与P中每一个集合做与运算，利用交集元件最多的2个集合pi(i=0，…，n)与nj(j=0，…，m)计算新极小冲突集pn+q(q初始为1，每计算一次q加1)，并将pn+q加入集合簇P中，而从集合簇N中将nj删除.以此类推，直至N为空时即可求出所有的极小冲突集，这时的极小冲突集的个数与系统输出的个数相同.

步骤3 对集合簇P中各集合中出现的所有l个元素，结合SE－Tree，按照宽度优先的搜索顺序，结合集合枚举的方法，并且按照元素个数逐步增多的顺序，逐一判断所枚举的当前的集合是否为集合簇的碰集，即通过计算该集合中所含各元素所关联的不同集合的总个数，由其值是否等于集合簇的长度m+n来确定.同时，在标准的SE－Tree计算过程中，加入某种节点标识(极小碰集节点(“√”)，终止节点(“×”)，待扩展节点(不加任何标识))，避免非极小碰集的产生，并从而提高搜索效率.

3 测点优选策略

在前面获取极小碰集的情况下，接下来将通过增加测点，获得相应的信息，减少极小碰集的数量.

3.1 测点优选算法

相关性模型法［6］正是在系统结构图的基础上，提出的一种单点故障诊断中测试点优选方法.其主要算法如下:

假设初选的测试点集合T具有n个测试点T=［T1T2T3… Tn］，被测试系统的故障状态集F包含了m个元件的单点故障状态F=［F1F2F3… Fm］，此时的相关性矩阵D0为一个m行n列的矩阵，矩阵中的元素dij表示第j个测试点Tj与第i个系统状态Fi的相关性，即

根据信息理论可知，利用矩阵D计算各个测试点所提供故障诊断综合信息量［7］.第j个测试点的故障诊断综合信息量I(tj)可表示为

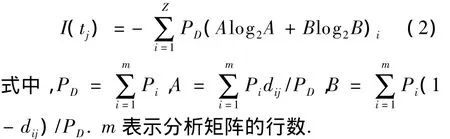
计算出各测试点的I(tj)之后，选用I(tj)值最大者对应的测试点Tj为第一个故障隔离用测试点，其对应的列矩阵为 Tj=［d1jd2j… dmj］T用Tj把矩阵D分为2个子矩阵，一个为(Tj中等于“0”的元素所对应的行构成的子矩阵);另一个为(Tj中等于“1”的元素所对应的行构成的子矩阵).

3.2 极小碰集去除规则

增加测点，如果测点处实际输出值与预测输出值相同，则相应的P－S子系统的部件所构成的是极小依赖集;反之，为极小冲突集.

由于极小碰集的元素个数为1或者2，因此极小碰集与新产生集合的交集元素个数只能为0、1或者2.

新增为极小冲突集时，当交集元素个数为0时，则表明实际故障元件不在此碰集中，删除该碰集;交集元素个数为1时，则表明实际故障元件有可能在碰集中，保留该碰集;交集元素个数为2时，不能判断这2个元件即为实际的故障元件，保留该碰集，进一步检验.

新增为极小依赖集时，当交集元素个数为0，则表明实际故障元件不在此碰集中，保留该碰集;交集元素个数为1时，则表明实际故障元件不在此碰集中，删除该碰集;交集元素个数为2时，不能判断这2个元件即为实际的故障元件，保留该碰集，进一步检验.

4 实例分析

7输入，2输出的九元件的模型系统，如图1所示，A，B，C，D，E，F，G，H 和 I分别为具有不同行为模式的元件.假设元件H发生故障，接下来将采用所提出的方法和策略快速而准确地进行故障定位.在这种假设下，系统输出O1的预测值和实际值是一致的，而系统输出O2的预测值和实际值是不一致的.根据命题2，能得出一个极小依赖集为{A，B，C，D，E，F}，极小冲突集为{B，C，E，G，H，I}.根据命题1，可以得到另一个极小冲突集为{A，D，F，G，H，I}.

图1 两输出系统模型框图

通过SE－tree方法，由极小冲突集簇P={{B，C，E，G，H，I}，{A，D，F，G，H，I}}可以计算出所有的极小碰集 H={{G}，{H}，{I}，{A，B}，{A，C}，{A，E}，{B，D}，{B，F}，{C，D}，{C，F}，{D，E}，{D，F}}.

假设系统部件发生故障的概率分别为P=［0.08 0.01 0.04 0.05 0.01 0.04 0.010.02 0.08］，系统的相关性矩阵及其故障隔离权值如表1所示.首先选择表1中WD值最大的测试点T7作为第一个故障检测用测试点.接着，选择I(tj)值最大的测试点T6(T7除外)作为第一个故障隔离用测试点，则利用相应的列矩阵 T'6=［d16d26… d96］T将相关性矩阵分割成2个矩阵和.然后，计算中的 I(tj)值，选择I(tj)值最大的测试点T4作为第二个故障隔离用测试点.继续分割矩阵，直到故障隔离用测试点的相应列矩阵不再包含“0”为止.最后测点优选的结果为 T7，T6，T4，T1.

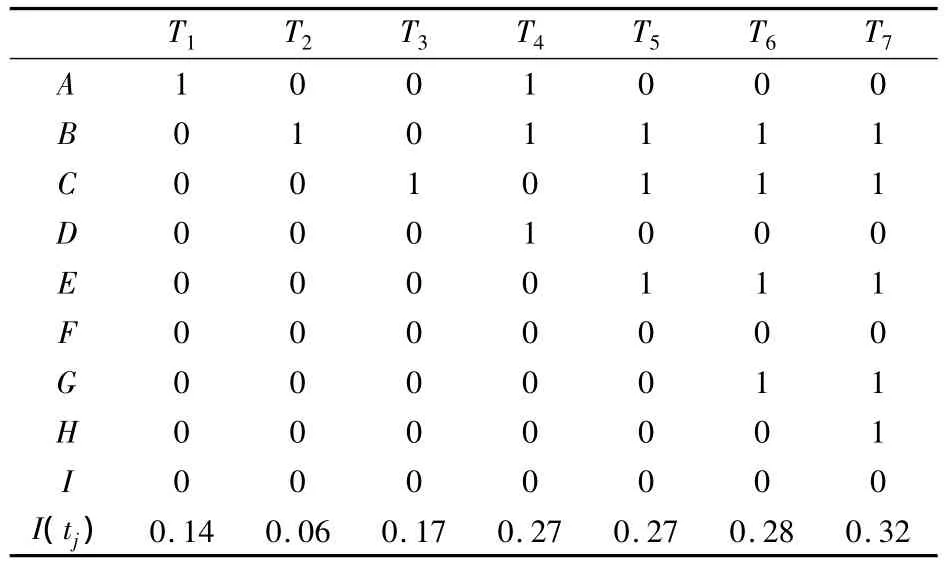
表1 相关性矩阵

故障定位的过程由表2所示，首先，加入系统测试点T7，由于T7相对应的P－S子系统的预测和实际输出值是不一致的，根据命题2，能得到一个极小冲突集{B，C，E，G，H}.然后，根据极小碰集去除规则，极小碰集{I}将被去除，则剩余极小碰集为 H1={{G}，{H}，{A，B}，{A，C}，{A，E}，{B，D}，{B，F}，{C，D}，{C，F}，{D，E}，{D，F}}.接着，加入系统测试点 T6，根据命题2，将得到一个极小依赖集{B，C，E，G}.最终，根据极小碰集去除规则{G}，{A，B}，{A，C}，{A，E}，{B，D}，{B，F}，{C，D}，{C，F}，{D，E}和{D，F}将被去除，最终H2={H}将被保留.从此结果可以看出，只需要加入2个测试点，根据测点优选策略，将实现故障定位.

表2 采用测点优选策略的故障定位过程

为了验证测点优选策略的速度和正确性，分别添加一个测试点，验证是否可以实现故障定位.如果是这样的话，那么本文所提出来的测点优选策略将不是最优的.由表3可以看出必须添加超过一个测试点才能实现故障的定位.

表3 加单一测点后所保留的极小碰集

5 结论

本文提出一种根据测点优选策略逐步实现故障定位的新方法.首先，利用SE－tree等算法，可以产生完备的用于故障定位的极小诊断候选集合.接着，通过引入相关性矩阵和故障诊断综合信息量，提出了测点优选策略.最后，提出极小碰集去除规则，通过增加测试点，最终完成了故障定位.实例表明，此方法是正确可行的，符合基于模型的故障诊断专家系统对于诊断的快速性和准确性的要求.

References)

［1］de Kleer J，Williams B C.Diagnosing multiple faults［J］.Artificial Intelligence，1987，32(1):97－130.

［2］Reiter R.A theory of diagnosis from first principles［J］.Artificial Intelligence，1987，32(1):57－96.

［3］Greiner R，Smith B A，Wilkerson R W.A correction to the algorithm in Reiter’s theory of diagnosis［J］.Artificial Intelligence，1989，41(1):79－88.赵相福，欧阳丹彤.可用于诊断产生的计算碰集的新方法［J］.吉林大学学报:理学版，2006，44(3):385－390.Zhao Xiangfu，Ouyang Dantong.A new method of computing hitting sets applied to diagnosis generation［J］.Journal of Jilin University:Science Edition，2006，44(3):385－390.(in Chinese)

［4］姜云飞，林笠.用布尔代数方法计算极小碰集［J］.计算机学报，2003，26(8):919－924.Jiang Yunfei，Lin Li.The computation of hitting sets with boolean formulas［J］.Chinese Journal of Computers，2003，26(8):919－924.(in Chinese)

［5］Ma C，Zhu D.Diagnostic method of causal network model based on swarm intelligence algorithm［C］//Intelligent Systems and Applications.Wuhan，China，2009:134－138.

［6］张立明，欧阳丹彤.一种基于ATMS的求解所有极小冲突集的新方法［J］.计算机工程与科学，2007，29(11):127－130.Zhang Liming，Ouyang Dantong.A new ATMS－based method for deriving all minimal conflict sets［J］.Computer Engineering and Science，2007，29(11):127－130.(in Chinese)

［7］周玉良，何广军.基于最大故障信息量准则的测试点优选方法［J］.弹箭与制导学报，2010，30(5):230－232.Zhou Yuliang，He Guangjun.An optimal method of selecting test point based on rule of maximum fault diagnosis information value［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2010，30(5):230－232.(in Chinese)