基于改进粒子群优化算法的弹道求解方法

崔静 邓方 方浩

(北京理工大学自动化学院，北京 100081)

(北京理工大学复杂系统智能控制与决策教育部重点实验室，北京 100081)

数字化技术的发展加快了未来战场节奏，对火控系统的实时性要求越来越高.为了提高火控系统的性能，有必要对外弹道的实时解算进行研究，缩短其所用的时间.目前，对射击诸元的求解方法主要有2种:射表逼近法与数值积分法.数值积分法因计算机技术的发展使得其大量计算变得容易而被广泛应用，不少学者对外弹道数值解算方法进行了研究.早期，周启煌等［1］提出了利用弹道的刚性原理进行射角迭代修正法;刘玉文等［2］给出了用2条积分弹道快速确定射角的方法;薛晓中等［3］提出了在弹道模型中加入权函数进行迭代修正解算的方法.近期，一些智能处理的方法被引入弹道解算中，如吕强等［4］将RBF网络应用于弹道解算中，将弹道解算时间缩短到10 ms，但是神经网络的前期训练需要大量的数据，并不具有普适性;刘彦君［5］采用改进遗传算法与龙格库塔法进行弹道求解，解算时间为0.1 s左右.在计算机技术突飞猛进的今日，尤其是多核计算机的大量出现，传统的采用串行结构的弹道求解方法，无法最大限度地发挥计算机的优势.而粒子群算法由于其粒子之间具有一定的独立性，可以较好地与并行计算相结合，采用多核计算机进行并行计算，有效缩短计算时间.此外，粒子群算法不仅收敛速度快且规则简单，在实际的运用中容易实现.因此，本文提出了基于迭代修正法的粒子群弹道解算方法.

1 外弹道模型及迭代修正法

目前，对于外弹道模型的研究已比较成熟，如文献［6］中给出了弹丸的简化4D模型及2D模型，周启煌等给出的2D模型［1］.本文采用文献［1］给出的外弹道微分方程组:

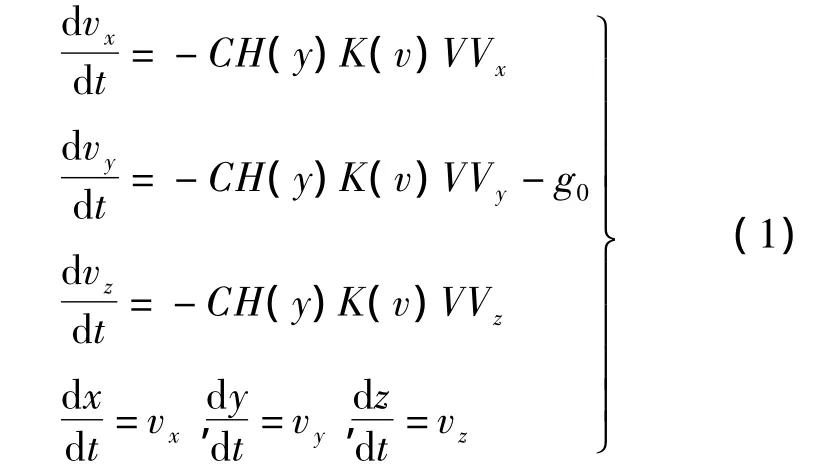
式中，C为弹道系数;H(y)为空气密度函数;K(v)为空气阻力函数.方程组的初始条件为 vx=v0cosα，vy=v0sinα，vz=0，x=0，y=0，z=0.

若已知射角与初始速度，则可采用数值积分法，如龙格库塔法求解出弹道轨迹曲线.实际中，则是已知目标距离与弹药初始速度来求解射角.文献［1］利用弹道的刚性原理，提出了迭代修正法，可以较快地求解出射角.其基本过程如下:

1)预估计瞄准角α0;

2)采用数值积分法(龙格库塔法)求解出弹药射程Di，计算Δxi=Di－D，其中D为目标实际距离;

3)判断是否满足Δxi＜ε，ε为事先定义的精度.若满足，则瞄准角为最终瞄准角.若不满足，则依据弹道刚性原理修正瞄准角，然后继续步骤2).

修正公式为

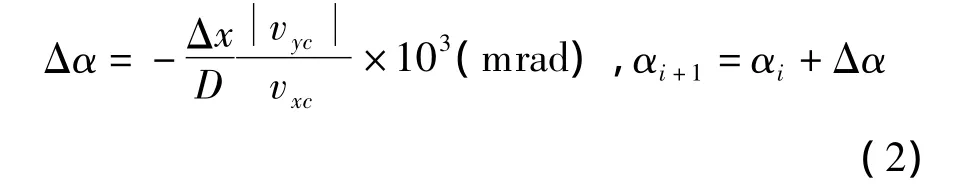
2 基于粒子群优化算法的弹道求解算法

随着多核计算机的应用范围越来越广，计算机对算法的性能和结构也提出了越来越高的要求.传统的算法产生在单核时期，串行结构无法有效利用多核计算机中所有的CPU.因此多核环境中并行计算可以更大程度地发挥多核计算机优势，相对于串行计算来说，可以成倍地减少计算时间.将多核计算机的并行计算引入弹道计算中，可以提高计算速度，提升火控系统的实时性.并行计算应满足2条原则:并行计算部分中的任务前后互不依赖;每个并行计算部分中的任务运行时间相同.迭代修正法中每次迭代是以上一次计算的结果为依据，不适用于并行计算，而粒子群算法中，每个粒子有各自的位置、速度、适应值，是相互独立的.因此，粒子群弹道解算本身不仅收敛速度快，规则简单、实现容易，而且可以更好地应用于并行计算中，有效利用多核计算机中所有的CPU.

2.1 粒子群优化算法

1995年，粒子群优化算法首先由Kennedy与Eberhart［7］提出.其思想来源于鸟类的觅食行为［8-9］.随机初始化一些没有质量和体积、只有速度的粒子，并将每一个粒子视为问题的一个可行解.粒子的适应度由一个事先定义的函数给出，决定了粒子的好坏.粒子在可行解空间中运动，其运动方向与距离由各自的速度决定.通常情况下，所有粒子将跟随当前最优粒子进行运动，然后进行逐代搜索更新，直至得到最优解.

假设由N个粒子组成的群体在D维空间内以一定的速度飞行.t时刻、粒子i的状态属性设置如下［8］:

式中，1≤d≤D，1≤i≤M.粒子 i在 t+1 时刻的位置更新公式如下:

式中，rand1，rand2为(0，1)区间内的随机数;c1，c2为学习因子.粒子群优化时首先初始化各个参数，并随机初始化粒子的位置与速度.然后计算每一个粒子的适应值，若满足精度要求则停止，否则进行粒子更新与下一次迭代.

2.2 粒子群弹道解算

粒子群优化算法引入弹道解算中，将允许范围内的每一个瞄准角视为弹道的可行解，根据瞄准角求出的射程d与期望距离D的差值的绝对值作为可行解的适应值.适应值越小则表示炮弹落点越接近目标，对应的瞄准角就越优.

假定目标的距离D已知，粒子群弹道解算过程如下:

1)初始化

一般可将初始瞄准角表示为距离D的二次函数［10］，即

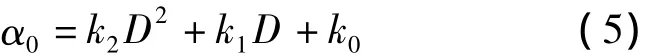
式中，ki，i=0，1，2 为按射表选择的系数.依据式(5)预估计瞄准角.然后在附近随机生成N个粒子()并随机初始化粒子的速度().

2)评价粒子

3)粒子状态更新

根据式(3)和(4)对每个粒子的位置与速度进行更新，得到)与

4)检验是否满足结束条件

判断Δxg＜ε(ε为弹道求解精度)是否成立.若成立，则当前全局最优位置为最终得到的瞄准角;若不成立，返回步骤2).

实验表明，粒子群弹道求解可以在较短时间内得到结果，但是由于粒子的随机性较大，粒子群更新次数浮动性很大.

2.3 改进的粒子群弹道解算方法

记弹道解算最优位置为αx，粒子群当前位置为，运用周氏迭代修正法求解其修正值.由弹道刚性原理可大概得到.则可得到

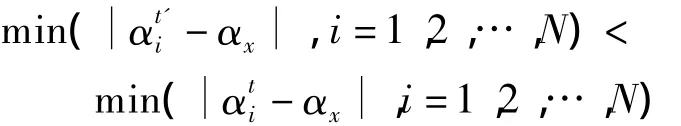
弹道解算基本过程与2.2节类似，差别在于在粒子群中假设一个隐含粒子x.在2.2节步骤2)中每个粒子由式(1)求解结果代入式(2)得到各自的修正位置，并记录全局最优位置所对应的修正位置为α'g，将(αg+α'g)作为x的位置.由弹道刚性原理可知，x的位置比全局最优位置更靠近最优点.在前述步骤3)中，本文用x的位置代替更新粒子的速度与位置，使得粒子更快地靠近最优解.改进粒子群弹道解算流程图如图1所示.

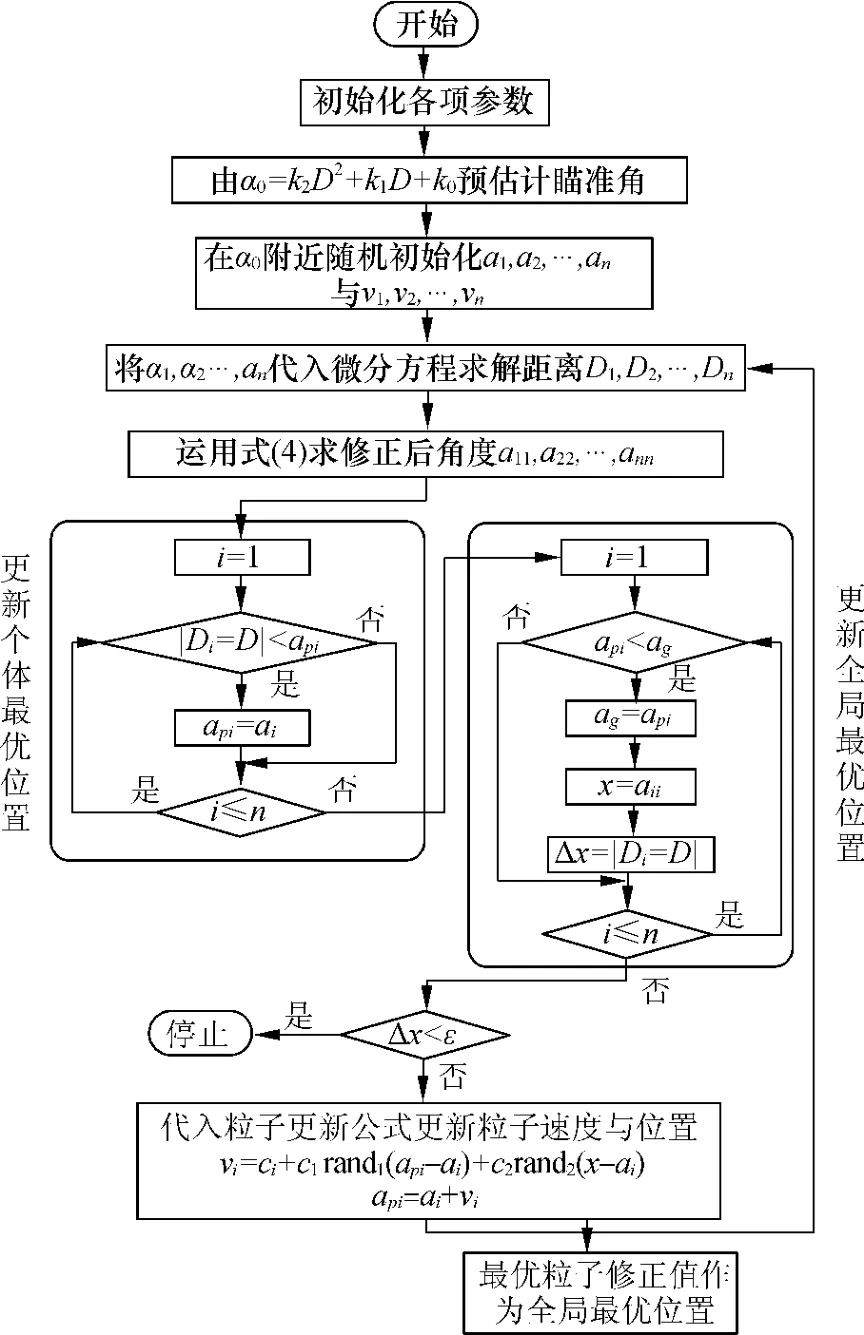
图1 改进粒子群弹道解算方法流程图

3 算例分析

本文采用某炮弹为例，其初速度为885 m/s，弹道质量为27.3 kg，最大射程23900 m，弹道系数C=0.52.采用标准气象条件，即地面虚温 288.9 K，地面大气压 1.206 kg/m3，海拔为 0 m.分别采用迭代修正法与本文提出基于迭代修正的粒子群算法进行解算.表1为实验结果，图2为迭代修正法、粒子群算法和改进后的粒子群算法程序运行时间动态图;图3为粒子群弹道解算与改进后粒子群弹道解算方法更新次数动态图.

由表1及图2可看出基于迭代修正的粒子群弹道解算方法中粒子收敛速度很快，计算时间快于传统的迭代修正法.从图3可看出引入迭代修正法后粒子的总体更新次数有所减少且波动范围缩小，缩短了求解所需时间.实验结果证明了本文提出的弹道解算方法的可行性与有效性.且此方法最大的优点是可以与并行计算很好地结合，在多核计算机平台下计算时间还可以进一步缩短.

表1 实验结果对比

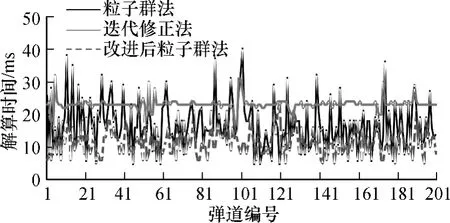
图2 弹道解算程序运行时间动态图

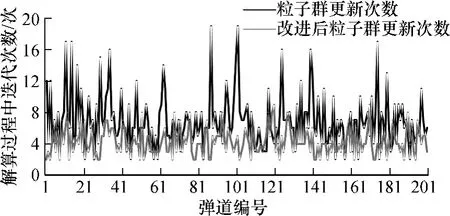
图3 两种粒子群弹道解算方法更新次数对比

4 结语

将粒子群优化算法运用于弹道求解中，并利用周氏迭代修正法加快粒子群算法的收敛速度，为实际的弹道求解提供了一种快速有效的方法.多核计算机的广泛应用，为大量数值计算提供了更快速的平台.传统的方法由于其结构的串行性，无法发挥多核并行计算的优势，而该方法可以很容易地扩展到多核计算机平台下进行并行计算，发挥多核计算的优势，大大减少弹道解算时间，提高火控系统的实时性.

References)

［1］周启煌，于谅，邱晓波.战车火控外弹道实时解算的研究［J］.火力与指挥控制，2001，26(4):15-18.Zhou Qihuang，Yu Liang，Qiu Xiaobo.Research on real-time ballistic for battle vehicles［J］.Fire Control and Command Control，2001，26(4):15-18.(in Chinese)

［2］刘玉文，杨启仁.快速确定火炮射角的一种方法［J］.弹道学报，1996，8(3):66-69.Liu Yuwen，Yang Qiren.A mathematical model of determining firing data by computer［J］.Journal of Ballistics，1996，8(3):66-69.(in Chinese)

［3］薛晓中，刘秀娟.权函数法在火控弹道模型中的应用［J］.兵工学报，1997，18(3):234-238.Xue Xiaozhong，Liu Xiujuan.Weighted function method for exterior ballistic modeling in fire control systems［J］.Acta Armamentarii，1997，18(3):234-238.(in Chinese)

［4］吕强，李建勋，周启煌.RBF网络用于战车火控系统弹道解算的方法［J］.火力与指挥控制，2007，32(4):26-28.Lv Qiang，Li Jianxun，Zhou Qihuang.Ballistic resolving algorithm of fire control system based on RBF neural network［J］.Fire Control and Command Control，2007，32(4):26-28.(in Chinese)

［5］刘彦君.基于改进的遗传算法与龙格库塔法的弹道求解方法［J］.兵工自动化，2011，30(1):4-7.Liu Yanjun.A method of ballistic based on genetic algorithm and Runge-Kutta［J］.Ordance Industry Automation，2011，30(1):4-7.(in Chinese)

［6］闫章更.射表技术［M］.北京:国防工业出版社，2000.

［7］Kennedy J，Eberhart R C.Partical swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Perth，Australia，1995:1942-1948.

［8］李丽，牛奔.粒子群优化算法［M］.北京:冶金工业出版社，2009.

［9］Eberhart R C，Kennedy J.A new optimizer using particle swarm theory［C］//Proceedings of the 6th International Symposium on Micro Machine and Human Science.Nagoya，Japan，1995:39-43.

［10］周启煌，东单升.坦克火力控制系统［M］.北京:国防工业出版社，1997.