极值波高Weibull分布的参数估计方法对比分析

王志旭，陈子燊

（中山大学 水资源与环境系，广东 广州 510275）

在海岸工程建设设计中，最重要的又难以决定的问题之一是设计波浪标准的选择，选用的设计波高有少量变化就会明显影响到工程的费用、涉及工程安全和维修方案。在得到波高长期样本数据后，可通过概率分布函数来拟合实测数据，并推算设计波高。Goda等 （1990）、Ferreira等 （2000）和Todd（2000）对各种分布函数做过分析比较，发现各种函数有其适用性。目前常用的分布函数有对数正态分布、Gumbel分布、皮尔逊Ⅲ型分布、Weibull分布。我国海港水文规范规定，对于年极值波高及其对应的周期的理论频率曲线，一般采用皮尔逊Ⅲ型曲线，也可以实测经验累积频率点拟合最佳为原则，选用其他理论频率曲线。

1927年，Fréchet首先给出威布尔分布的定义，即极值Ⅲ型分布。Rosin等（1933）在研究碎末的分布时，第一次应用了威布尔分布。1951年，瑞典工程师、数学家Weibull通过研究轴承寿命、结构强度和疲劳等问题从而详细解释了这一分布，于是，该分布便以他的名字命名为Weibull distribution。随后，威布尔分布广泛应用于质量管理上的元件和材料寿命可靠性研究，是可靠性分析和寿命检验的理论基础。1954年Gumbel将其应用到年最枯流量的水文统计分析中，Neelamani等（2007）和Seguro等（2000）分别将其应用于风速和波高的极值推算。

1 Weibull分布与参数估计方法

威布尔曲线的概率密度函数为：

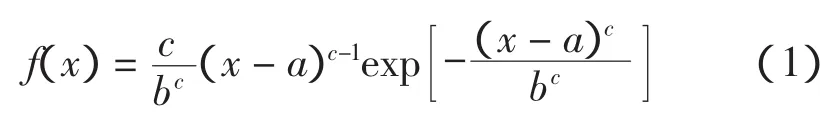
分布函数为：

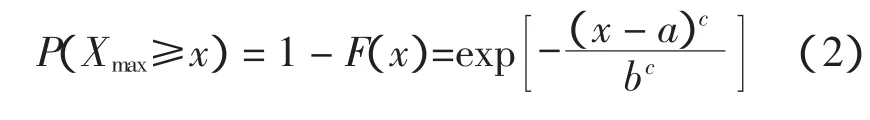
式中，a≥0，为位置参数；b＞0，为尺度参数；c＞0，为形状参数；x≥a。

三参数威布尔分布型式具有较大灵活性，形状参数的存在使其在数据拟合上极富弹性，比二参数威布尔分布有更高的拟合精度，然而其参数的优良估计比较复杂。对于威布尔分布的参数估计，国内外有众多学者进行相关研究，传统的参数估计方法有极大似然估计法、最小二乘法、矩估计法等。我国学者相继提出了双线形回归法（庄渭峰，1999）、概率权重矩法（张秀芝，1994）、相关系数优化法（傅惠民等，1990；史景钊等，1995）和灰色估计法（郑荣跃等，1989）。不过，各方法存在着相应的优缺点，各自的使用范围和精度也都不同。本文利用蒙特卡罗法对常用的4种参数方法（极大似然法、概率权重矩法、相关系数优化法和灰色估计法）进行模拟，讨论各方法的适用性及其精度，并用上述各种参数估计方法对涠洲站34年实测年极值波高进行设计波高的推算，分析其优良性。

1.1 极大似然估计法

极大似然估计（Maximum Likelihood Estimation，MLE）的基本思想是选择待定参数使样本出现在观测值的领域内的概率最大，并以这个值作为未知参数的点估计值（朱勇华等，1999）。

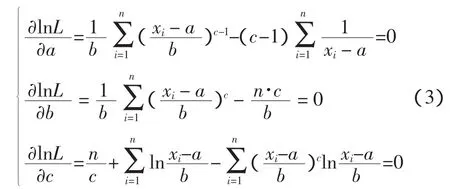
对于此超越方程组有多种算法，本文采用王华胜等（2004）提出的求解方法。

1.2 相关系数优化法

相关系数优化法（Correlation Coefficient Method，CCM）是我国学者史景钊等（1995）提出的一种估计威布尔分布位置参数的新方法，对式（2）进行变换得：

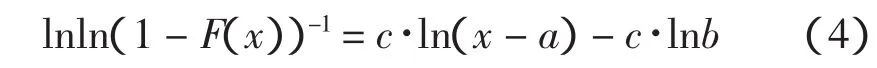
上式可以简化为线性方程

将获取的极值波高序列从小到大排列得到序列xi，通过极值波高累计率估计量F（xi）计算得到序列Y，由式（4）、（5）可知，如果位置参数a估计正确，X、Y将呈线性关系，即X、Y之间有着最大的相关系数。

根据这个思路，可以给定a一个初始值（略小于波高序列最小值）和一个步长（步长可根据实际数据进行设定），a按步长递增可得一系列的X与Y的相关系数R2。a与R2的关系为：随着a的增加，R2先增后减，当R2达到最大值时，此时的a为最佳理论估计值。

另外可以通过推导证明，在下式成立时，相关系数R2最大：

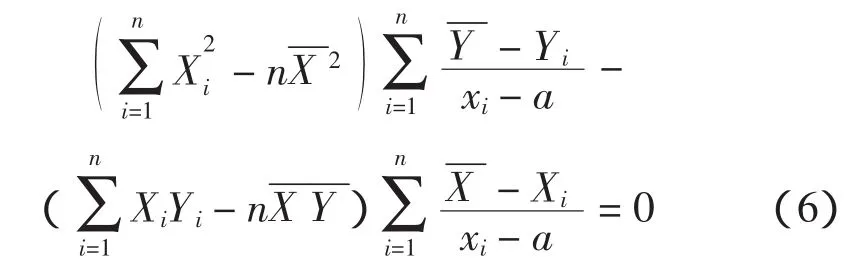
用相关系数法求出位置参数a后，c和B的参数估计可用最小二乘法或其他方法进行估计。

1.3 灰色估计法

灰色估计法是郑荣跃等（1989）基于邓聚龙提出的灰色系统理论发展的一种较新的参数估计方法。在已知数列（如波高、风速序列）前提下，以单数列的微分方程GM（1，1）为基础，得到各类灰色预测方法，通过预测方法进行参数估计。

式 （1-2）可变换为：

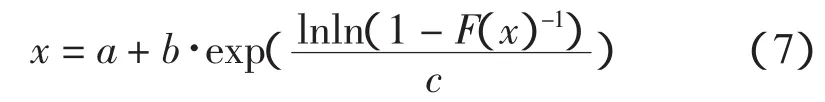
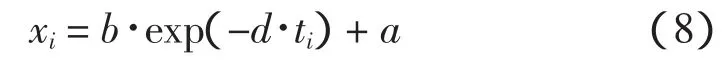
式 （8）对应于灰色估计GM（1，1）的时间响应模型：

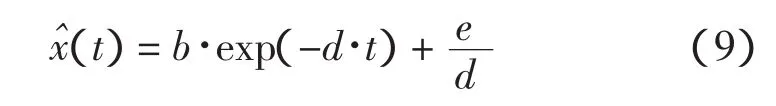
从而可用GM（1，1）模型对参数a，b，e，d进行估计，再由此得到威布尔分布三参数的估计值（其中，c=-1/d）。灰色估计的参数为：

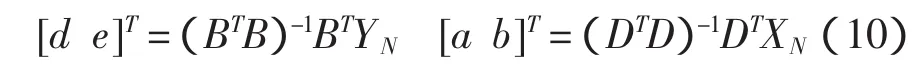
式中：

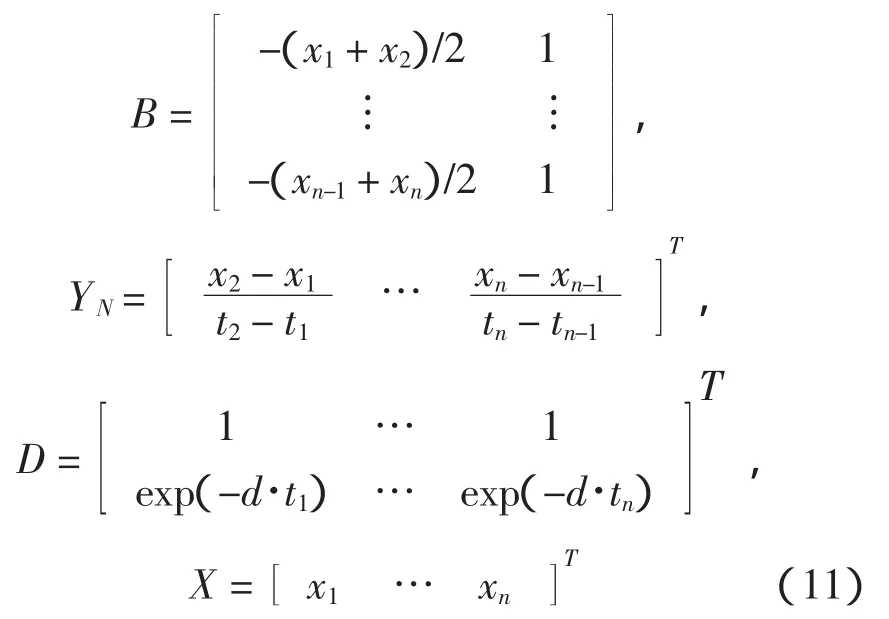
1.4 概率权重矩法

Greenwood等（1979）提出了概率权重矩法（Probability Weighted Moments，PWM），并应用于Gumbel、GEV和Wakeby分布的参数估计。张秀芝（1994）将其运用于三参数Weibull分布的参数估计，并推算了极值风速。样本的概率权重矩估计值为：

其中，Pi为对应于xi的累积频率。用概率权重矩表示的威布尔分布参数估计值为：

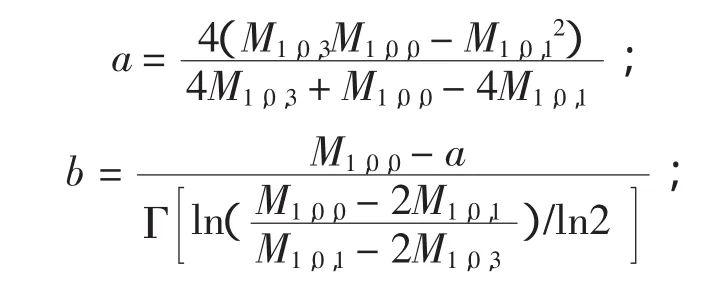
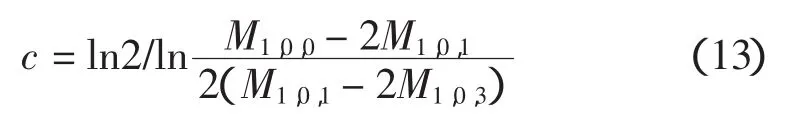
2 参数估计方法分析比较

利用蒙特卡罗模拟方法对以上4种参数估计方法进行参数估计并分析其优劣性、适用性。为使计算估计结果更加精确，本文中蒙特卡罗模拟运行次数J=5 000，样本数分别取20、50、100、200、500，选取参数估计量的偏差、标准差和均方误差来评价估计结果。估计参数的偏差、标准差和均方误差越小，估计方法越好。威布尔分布三参数的估计值为，令待估参数 a=20，b=30，c=2.5，模拟结果见表1：

（1）通过偏差、标准差和均方误差的对比，对于不同样本大小，极大似然估计法参数估计结果较好，相关系数法次之，灰色估计法的效果最差。当样本数越来越大时，各种参数估计方法的结果差异逐渐缩小。

（2）灰色估计法在小样本时即可建模；概率权矩法和灰色估计法计算简单，避免了试定和迭代等复杂计算，然而在小样本时难以得到良好参数估计；相关系数法假定位置参数是独立的，虽能得到最佳的位置参数估计，但忽略了位置参数与形状参数、尺度参数的相关性，尽管有此缺陷，其估计所得的参数仍有较高精度；极大似然估计法算法最为复杂，需要进行试定和迭代计算。

（3）概率权矩法、灰色估计法、相关系数法均受样本元素经验概率Pi影响。Pi取值不同，估算精度也有所差别。对于概率权重矩法，Hosking（1985）认为可采用估算值：Pi=（i-0.35）/n。表1各种参数估计方法均采用此公式。

为分析不同参数估计方法适用的经验频率，采用以下多种经验频率公式（黄振平，等，2002）进行蒙特卡罗模拟：海森公式：Pi=（i-0.5）/n；数学期望公式：Pi=i/（n+1）；中值公式：Pi=（i-0.3）/（n+0.4）；Blom公式：Pi=（i-0.375）/（n+0.25）；Tukey公式：Pi=（3i-1）/（3n+1）；Gringorten公式：Pi=（i-0.44）/（n+0.12）。结果表明：灰色估计法采用海森公式时，计算结果精度较好，也相对稳定；概率权重矩法仍采用上述公式；采用海森公式和Gringorten公式进行相关系数优化法参数估计所得的结果相差很小，但均优于其他经验频率公式所得结果。

表1 蒙特卡罗模拟不同样本长度与不同参数估计的误差

3 设计波高推算

以涠洲站东（E）向浪34a的年最大波高为样本（夏华永等，2001）其中最大波高为5.3m，最小波高为0.9m，平均波高为2.85m，利用上述各种三参数威布尔分布的参数估计方法进行设计波高的推算，其中相关系数优化法和灰色估计法的经验频率公式使用海森公式，概率权重矩法采用Pi=（i-0.35）/n。为使实测波高与Weibull分布拟合有着更直观的线性对比，对式（2）进行变换，得Weibull简化变量W：

各种参数估计方法拟合的结果见图1。利用相关系数R、均方根误差和Q统计值来分析比较各种参数估计结果的优良性。1）均方根误差：

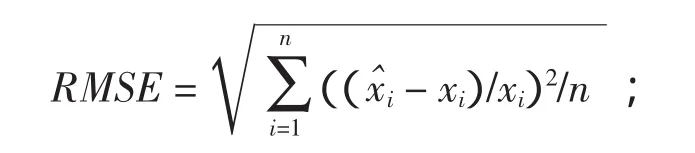
2）Q统计值：

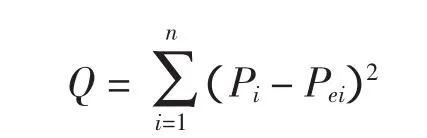
式中：xi为实测样本序列排序后观测值和经验累积频率分布Pei计算的与威布尔分布相应的分位数；Pi：理论累积频率；n：样本容量。在样本容量相同的情况下均方根误差和Q值越小，拟合越好。

由表2可知，极大似然估计法的相关系数最大且Q统计值最小，相关系数法的均方根误差最小。各估计方法均估算得良好的参数，使得波高数据的拟合具有最好的线性度（图1），综合而言，极大似然估计法所得结果更加精确。相关系数优化法与灰色估计法所得的三参数大小均相差较大，推算而得的H1%相差达0.22m；而概率权矩法和极大似然估计法参数差异较小。采用极大似然估计法计算结果，涠洲岛50年一遇极值波高为4.98m，100年一遇极值波高为5.27m。1992年涠洲站年极值波高为5.3m，达到100年一遇。

图1 三参数W eibu ll分布线性拟合结果

表2 不同参数估计方法的设计波高推算结果

4 结论

（1）对于各种容量的样本，极大似然估计法参数估计结果精度较好，然而在小样本时（n=20），各种估计方法所得结果均不理想，偏离实际参数较大。随着样本容量的增加，各种估计方法之间的差异越来越小，当样本容量大于100时，各方法所得结果已很接近。

（2）需选用合适的样本元素经验概率Pi，以保证取得较好的参数估计，其中相关系数法和灰色估计法宜采用海森公式，概率权矩法采用Pi=1-（i-0.35）/n。

（3）一般年极值波高序列样本长度有限（少于50年），进行设计波高推算时可采用精度较高的极大似然估计法，也可根据实际情况进行估计方法分析对比，选择合适的估计方法。

（4）利用极大似然法估计威布尔分布三参数，推算而得涠洲岛50年一遇极值波高为4.98m，100年一遇极值波高为5.27m。在34年的年极值波高序列中，1992年的年极值波高达到了100年一遇。

Ferreira J A，Guedes S C，2000.Modelling distributions of significant waveheight.CoastalEngineering，4（40）：361-374.

Goda Y，KobuneK，1990.Distribution function fitting forstorm wave data.Proceedingsof the22nd InternationalConferenceon Coastal Engineering，ASCE，18-31.

Greenwood J A，Landwehr JM，Matalas N C，et al，1979.Probability Weighted Moments：Definition and Relation to Parametersof Several Distributions Expressible in Inverse Form.Water Resources Research，15（5）：1049-1054.

Hosking JR M，Wallis JR，Wood E F，1985.Estimation of the generalized extreme value distribution by themethod of probability weight-ed moments.Technometrics，27（3）：251-261.

Neelamani S，Al-Salem K，Rakha K，2007.Extreme waves for Kuwaiti territorial waters.Ocean Engineering，34（10）：1496-1504.

Rosin P，Ramm ler E，1933.The laws governing the fineness of powdered coal.Journalof the Instituteof Fuel，7：29-36.

Seguro JV，Lambert TW，2000.Modern estimation of the parameters of the Weibullwind speed distribution for wind energy analysis.Journal of Wind Engineeringand Industrial Aerodynamics，1（85）：75-84.

Todd L，2000.Distributions for storm surge extremes.Ocean Engineering，27（12）：1279-1293.

傅惠民，高镇同，1990.确定威布尔分布三参数的相关系数优化法.航空学报，11（7）：323-327.

黄振平，萨迪伊，王春霞，等，2002。关于适线法中经验频率计算公式的对比研究.水利水电科技进展，22（5）：5-8

史景钊，蒋国良，1995.用相关系数法估计威布尔分布的位置参数.河南农业大学学报，29（2）：167-171.

王华胜，李忠厚，林荣文，等，2004.耗损故障的三参数Weibull分布极大似然估计方法.中国铁道科学，25（5）：39-42.

夏华永，李树华，2001.广西沿海年极值波高分析.热带海洋学报，20（2）：1-7.

张秀芝，1994.概率权重矩法及其在Weibull分布参数估计中的应用.海洋预报，11（3）：55-61.

郑荣跃，秦子增，1989.Weibull分布参数估计的灰色方法.强度与环境，（2）：34-40.

朱勇华，邰淑彩，1999．应用数理统计．武汉：武汉水利电力大学出版社.

庄渭峰，1999.用微机实现威布尔参数的双线性回归最小二乘估计.电子产品可靠性与环境试验，5：2-7.