认知无线电系统的最优帧长设计＊

胡志刚，汤海冰

（中南大学 信息科学与工程学院，湖南 长沙 410083）

目前无线频谱已经相当拥挤[1]，有耗尽的风险.但对各个频带占用情况的统计结果表明[2]，3GHz以下频段的频谱资源占用率普遍较低，造成了频谱资源的严重浪费.究其原因，主要是由于对频谱资源实行固定授权分配机制.J.Mitola最早提出了认知无线电（Cognitive Radio，CR）的概念，其要点是认知用户（从用户）检测授权用户（也叫主用户）不占用其频谱时形成的“频谱空穴”，并利用这些空穴进行通信；而当主用户使用这些频谱时，认知用户必须及时退出.

认知无线电系统在Mac层一般采用帧结构的方式，认知无线电系统的帧长主要由感知时间和数据发送时间组成.目前，关于认知无线电系统的帧结构[3－5]主要研究集中在感知时间的优化和数据发送时间的固定.文献[6－7]主要研究了一次感知多个信道情况下，感知时间的优化问题.以上文献都没有考虑主用户的活动情况，如果主用户到达率过大，认知用户的服务质量就可能得不到保证；同样，如果帧长过长，则可能由于认知用户的干扰，主用户的服务质量得不到保证.理想的情况是根据主用户的活动，设置最优帧长：感知时间和数据发送时间.文献[8]研究了主用户活动统计特性对认知网络吞吐量的影响，但其并没有研究帧长的优化问题.文献[9]研究了主用户对信道的占用／空闲（on／off）时间服从负指数分布、认知网络吞吐量最大时的最优帧长，但其假设认知用户在使用数据发送时间时，即使主用户到达，仍然占用整个数据发送时间，并不退出，也没有对感知时间进行优化.文献[10]基于主用户对信道的占用／空闲时间服从负指数分布，研究了当最优化感知效率（即认知用户发送时间占帧长的百分比）且干扰率满足约束时，感知时间和数据发送时间的优化问题，但其假设虚警概率等于误检概率，这不能满足一些应用对虚警概率和误检概率不等权需求的情况.

本文首先将虚警概率和误检概率加权定义成贝叶斯风险，研究了当贝叶斯风险一定时，干扰率与发送时间的关系.在此基础上，提出了2种满足干扰约束的算法：单用户感知模式下最大化系统吞吐量时的帧长设计算法和多用户合作感知模式下基于纽曼－皮尔逊准则的帧长设计算法.这2种算法的目的是对感知时间和数据发送时间的优化.

1 系统模型及问题描述

1.1 单用户感知系统模型

本文采用帧结构的认知无线电系统，认知用户基于overlay模式接入，假定每帧长感知一个信道，噪声为高斯白噪声.对主用户的活动情况，假设主用户任务对信道占用忙时间服从参数为α的负指数分布，信道空闲时间服从参数为β的负指数分布，则由排队论可知：

式中：Pon和Poff分别为主用户信道忙和空闲的概率.认知用户每隔一个帧长周期检测主用户信号是否存在，接收信号可写成二元假设形式[10]：r（t）＝hs（t）＋n（t），当h＝0时，表示主用户信号不存在；当h＝1时，表示主用户信号存在；其中n（t）表示均值为零，方差为σ2n的高斯白噪声.σ2s为主用户信号s（t）的方差.本文采用能量检测，则基于主用户活动模型的检测概率Pd（λ，ts）和虚警概率Pf（λ，ts）可表示为[10]：

式中：（λ，ts）和（λ，ts）分别为能量检测方式下的检测概率和虚警概率；ts为感知时间.

式中：Q（x）为高斯补函数.

1.2 问题描述

针对上述给定的系统模型，本文的目标是解决当贝叶斯风险一定、干扰率控制在阈值内时，最大化认知用户的吞吐量情况下，认知网络帧长的最优设计问题.

认知用户的吞吐量可表示为：

式中：C为根据香农公式得出的信道容量，这里为常量.用（λ，ts）表示误检概率，在感知模型下，贝叶斯风险描述为，其优势是可根据实际需要决定虚警概率与误检概率的权重c1，c2.由于，贝叶斯风险又可表示为：

当（λ，ts）＝1时，（λ，ts）取最大值：

当主用户对信道的占用／空闲服从负指数分布时，根据文献[10]中干扰率计算公式，可得出主用户与认知用户的干扰率为：

式中：μ＝max（a，β）；T为一帧中数据发送时间；TI（T）即帧长为T时，主从用户互相干扰的概率，一般要求这个干扰率低于某一门限Tp.

综上，本文的目标可表述成一个最优化问题P1.

2 分析与求解

本节求解最优化问题P1.由于目标函数非凸，一般的最优化方法如牛顿法、罚点函数法等难以求得全局最优解，且求得局部最优解也同初值密切相关.本文首先把问题P1的约束转化为等价的式（13）和 式（14），巧妙建立了贝叶斯风险下帧长与虚警概率间的关系式（13），通过定理1及式（8）得出了（λ，ts）的取值区间式（16），再根据（λ，ts）取值区间较小的特点，提出了一个复杂度较低的算法.

由式（3）和式（4）可得：

将式（11）代入式（7）得：

将式（9）和式（7）代入式（10），化简可得：

令

定理1F（T）有最小值.

证 令x＝e－μT，因为x是关于T的单调函数且0≤x≤1，给定c1，c2，Poff，Pon和Tp时，对F（x）求导，可得F′（x）分子为x的一次函数，而分母总大于0.所以其最小值总在F（0），F（∞）或F′（T）＝0处.其具体位置由给定的c1，c2，Poff，Pon，Tp决定.证毕.

根据定理1，令

结合式（8）有：

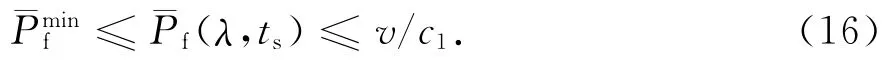
对于某个（λ，ts）值，可根据式（14）和式（15）解得ts和T，代入式（7）解得吞吐量值R（λ，T，ts）.根据式（7），c1，考虑到实际取值时虚警与误检概率的权重分配不会相差太大（即c1，c2的比值不会大太或太小）.所以（λ，ts）的取值区间一般较小.因而可采用穷举搜索，以步长Δ搜索所有可能的（λ，ts），考虑到实际需求，可设Δ＝0.001，求得最大吞吐量.根据以上分析，求解T＊，t＊s，λ＊的算法如下：

算法1 对于最优化问题P1的求解：

1）根据式（15）确定.赋初值＝；

2）while（≤v／c1，步长Δ＝0.001）；

根据式（12），解得ts；

根据式（13），解得T；

根据式（6），解得R（λ，T，ts）；

保存当前最大吞吐量R＊及应对的，T＊，t＊s.

3）将，t＊s代入式（3），解得λ＊.

3 纽曼－皮尔逊准则下最优帧长算法

合作频谱感知已经有了许多研究文献[11－13]，但很少有将感知时间和数据发送时间进行联合优化的研究.本节讨论当合作频谱感知时，纽曼－皮尔逊准则下的最优帧长.考虑到求解的复杂性，这里仅考虑λ已知时的情况，此时，记为.问题P2可描述如下：

其中：

当认知用户N中超过K个用户判决一致时，判决成立.

为求解问题P2，本文先证明以下定理及推论.

定理2Qd是关于¯Pd的递增函数，Qf是关于¯Pf的递增函数，且当¯Pd＜K／（N－1）时，Qd为凸函数.当¯Pd＞K／（N－1）时，Qd为凹函数.

根据式（19）可知，U（x）为递增函数；根据式（20）当x＜K／（N－1）时，U（x）为凸函数；当x＞K／（N－1）时，U（x）为凹函数.

推论1 给定λ，则均是关于ts的递增函数.

同理可证（ts）是关于ts的递增函数.

推论2Qd是关于ts的递增函数.

证 根据定理2，Qd是的递增函数，根据推论1，是ts的递增函数，所以Qd是关于ts的递增函数.证毕.

定理3Qd是关于Qf的递增函数.

问题P2的求解思路是利用Newton－Raphson算法，解式（17）中的等式约束，得，根据定理3，此时Qd取最大值；再根据式（3），解得ts的上限值，而根据定理2，此时Qd取最大值.所以ts的上限值即为纽曼－皮尔逊准则下的最优值ts.最后根据式（9），显然，当，确定时，TI（T）为递增函数，所以Tminp＝TI（0）＝1－¯Pd（ts）.综上，给出纽曼－皮尔逊准则下的最优帧长算法.

算法2 问题P2的求解算法.

1）根据Newton－Raphson算法，解式（17），得.

2）将代入式（3），解得t＊s；将t＊s代入式（4），解得（λ，ts）.

3）如果Tp＜1－（λ，ts），则无解；否则，根据式（9），解得T＊.

考虑到Newton－Raphson算法的复杂度可能与初值相关，因为Qf是关于¯Pf的递增函数，所以也可用二分法[14]来求解¯Pf.图1为在不同K值下Qd随ts的变化曲线.图2为满足约束Qf≤0.1时，根据算法2求解的不同K值对应的最大Qd.由图2可知，K＝2时的最优值大于K＝1时的最优值，这是因为当K＝1时，ts值相对较小.

图1 协作时检测概率随感知时间的变化Fig.1 The change of the detection probability with the sensing time in cooperative sensing mode

4 仿真与性能分析

为了验证帧长对干扰和吞吐量的影响，通过Matlab进行了仿真实验.实验基本设置为：α＝1，β＝2，B＝10kHz，Tp＝0.05，σ2n＝1，snr＝－5dB，c1＝1，c2＝1.

首先仿真了Lee的最优帧长算法[10]与本文算法1.表1为干扰时间（共进行300s仿真）、最优帧长及最优帧长下吞吐量等参数的对比.

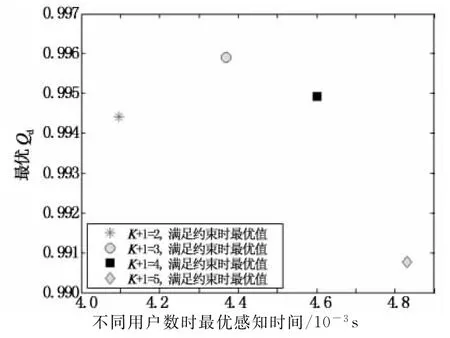
图2 不同K值时最大协作检测概率Fig.2 The largest cooperative detection probability for differentK

由表1可知，2种算法在干扰率上相差不大，满足干扰门限要求，但本文算法在发送时间、感知时间参数上优于Lee算法.正是这一点，即使在风险值v较大的情况下，本文算法在吞吐量上优于Lee算法.

图3为v＝0.15时感知时间、发送时间及帧长与吞吐量的关系曲线.由图3可知，帧长在0.750s左右下降较大，这主要是因为数据发送时间T增加非常缓慢的缘故.需要指出的是虽然这时吞吐量同Lee算法比相差不大，但这只是风险值较大的情况.

图3 当v＝0.15时帧长与吞吐量的关系Fig.3 The relationship between the frame size and throughput whenv＝0.15

表1 仿真结果参数对比Tab.1 Parameter comparison of the simulation results

图4为v值对吞吐量的影响.由图4可知，随着风险值减小，吞吐量急剧提升.图5为风险值v与最优帧长的关系.由图4和图5可以看出，风险值对吞吐量和最优帧长均有较大影响，因为在实验基本设置下，根据式（13），（15）和（16）可得，v－Tp≤¯Pf（λ，ts）≤v，可以看出，Tp较小时，v变化对¯Pf（λ，ts）影响较大，进而影响吞吐量和最优帧长.而由式（12）和式（13），¯Pf（λ，ts）对t＊s和T＊的影响是非线性的，即对最优帧长的影响是非线性的.具体的实验参数导致在v＝0.14时，最优帧长出现了一个拐点.

图4 贝叶斯风险值对吞吐量的影响Fig.4 Bayesian risk value′s influence on throughput

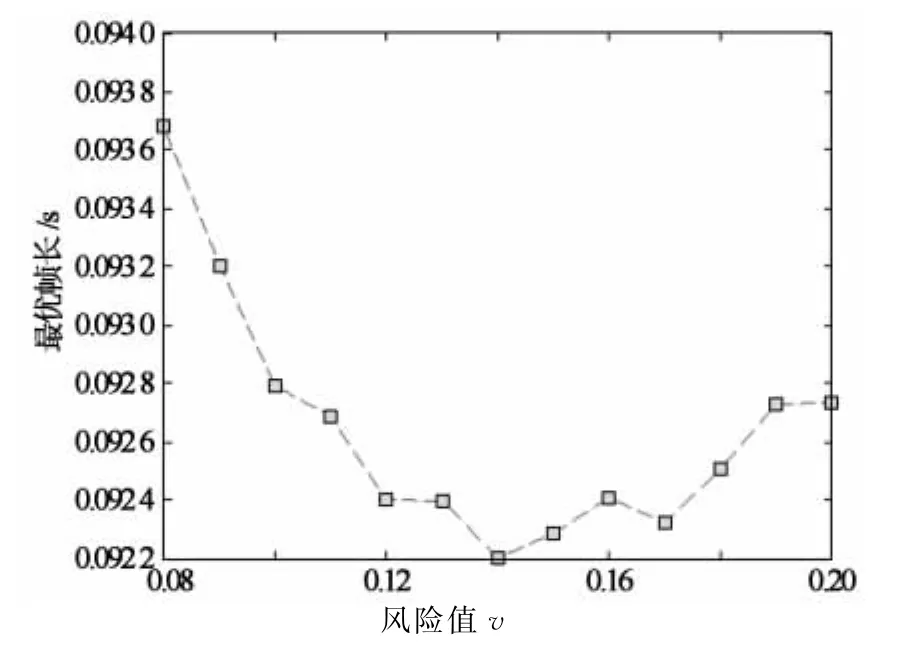
图5 风险值与最优帧长的关系曲线Fig.5 Bayesian risk value and the optimal frame length

5 结 论

本文针对帧结构认知无线电系统，如果帧长设计不当，容易引起干扰的问题，提出一种满足干扰约束，指定贝叶斯风险时判决门限、认知用户感知时间和数据发送时间的联合优化算法，并研究了多用户协作感知时帧长的优化问题.仿真结果表明，在同样的干扰约束下，同现有的帧长设计算法相比，本文算法有更优的帧长，而且即使在贝叶斯风险较大时亦有更优的吞吐量.

[1] AKYILDIZ I F，WON－YEOL L，MEHMET C V，etal.NeXt generation／dynamic spectrum access／cognitive radio wireless networks：a survey[J].Computer Networks，2006，50（5）：2127－2159.

[2] AKYILDIZ I F，WON－YEOL L，MEHMET C V，etal.A survey on spectrum management in cognitive radio networks[J].IEEE Communications Magazine，2008，46（4）：40－48.

[3] LEE D J，JANG M S.Optimal spectrum sensing time considering spectrum handoff due to false alarm in cognitive radio networks[J].IEEE Communications Letters，2009，13（12）：899－901.

[4] KIM I，KIM D W.Optimal allocation of sensing time between two primary channels in cognitive radio networks[J].IEEE Communications Letters，2010，14（4）：297－299.

[5] JIAN H，XU C Q，LI L.Joint optimization of sensing time and decision thresholds for wideband cognitive OFDM radio networks[C]／／Wireless，Mobile and Multimedia Networks（ICWMNN 2010）：IET 3rdInternational Conference on.Beijing：IEEE，2010：230－233.

[6] YAO H P，SUN X，ZHOU Z.Joint optimization of subchannel selection and spectrum sensing time for multiband cognitive radio networks[C]／／Communications and Information Technologies（ISCIT）：2010International Symposium on.Tokyo：IEEE，2010：1211－1216.

[7] STOTAS S，NALLANATHAN A.Optimal sensing time and power allocation in multiband cognitive radio networks[J].IEEE Transactions on Communications，2011，59（1）：226－235.

[8] HOSSEINI S M，TEIMOURI M.Mathematical analysis of primary users characteristics effects on cognitive radios[C]／／ICACT：2010the 12thInternational Conference on Gangwon－Do.Korea（South）：IEEE，2010：1252－1255.

[9] PEI Y Y，HOANG A T，LIANG Y C.Sensing－throughput trade off in cognitive radio networks：how frequently should spectrum sensing be carried out？[C]／／PIMRC’07.Athens，Greece：IEEE，2007：1－5.

[10] LEE W Y，AKYILDIZ I F.Optimal spectrum sensing framework for cognitive radio networks for cognitive radio networks[J].IEEE Transactions on Wireless Communications，2008，7（10）：3845－3857.

[11] PEH E，LIANG Ying－chang.Optimization for cooperative sensing in cognitive radio networks[C]／／ Wireless Communications and Networking Conference.Kowloon：IEEE，2007：27－32.

[12] ZHANG W，MALLIK R K，LETAIEF K B.Optimization of cooperative spectrum sensing with energy detection in cognitive radio networks[J].IEEE Transactions on Wireless Communications，2009，8（12）：5761－5766.

[13] FEI R，JIANG H.Optimal multi－channel cooperative sensing in cognitive radio networks[J].IEEE Transactions on Wireless Communications，2010，9（3）：1128－1138.

[14] SHEN J，LIU S，ZENG L，etal.Optimization of cooperative spectrum sensing in cognitive radio network[J].IET Communications，2009，3（7）：1170－1178.