新的基于内置式永磁同步电机的弱磁控制策略＊

黄守道，徐 琼，祁 宙，李建业，杜 超，郭灯塔

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082； 2.海上风力发电技术与检测国家重点实验室，湖南 湘潭 411101）

内置式永磁同步电机（Interior Permanent Magnet Synchronous Motor，IPMSM）以高效率、高功率密度和调速范围宽等优点，广泛应用于各种电机驱动系统中，如电动汽车、轨道机车、机器人等领域.在这些应用中，不仅要求较宽的弱磁调速范围，而且要求较强的弱磁性能[1－4].较强的弱磁性能可在逆变器容量不变情况下提高系统性能[1－8].

基于弱磁扩速的基本思想，国内外研究者提出了许多用于改善永磁同步电机弱磁性能的控制策略.文献[1]提出了前馈弱磁控制方法，有较好的稳态性能，但易受电机参数及温度变化的影响，鲁棒性差.文献[2－3]提出了直流侧电压环反馈调节方法，鲁棒性好，但逆变器的直流母线电压没有被完全利用.为了最大程度利用母线电压，文献[4]采用六步电压过调制法，然而会产生很大电流谐波，且通过前馈查表法来调节电流，算法复杂.

本文阐述了内置式永磁同步电机的弱磁运行原理，分析了传统弱磁控制算法中直流母线电压没有完全利用的不足之处，提出了一种新的弱磁控制策略，通过用SVPWM调制前后输出的电压差值来改变电流相位角从而调节交直轴电流.仿真和实验结果证明该改进算法实现了电机高倍基速以上的稳定运行、弱磁电流过渡平滑，对比传统弱磁算法，在同样条件下，电机在弱磁区域能输出更大电磁转矩.

1 IPMSM的弱磁原理

内置式永磁同步电机在两相同步旋转d，q坐标系下的稳态电压方程为：

电机高速运行时，定子电阻压降较小，可忽略不计，式（1）可以表示为：

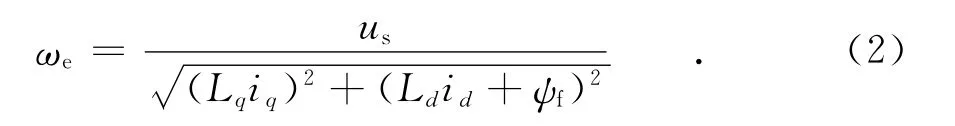
IPMSM最优控制运行的定子电流变化轨迹如图1所示.基速以下，采用最大转矩电流比（maximum torque per ampere，MTPA）控制可使永磁同步电机获得最大电磁转矩，如图1中OA段.随着转速继续上升，电机运行于A点时电机端电压达到逆变器所提供的极限电压，电机无法继续往高速运行.由式（2）可知，只有通过调节定子电流，即增加直轴电流分量，同时减小交轴电流分量来实现弱磁升速[5－6].为最大限度利用逆变器容量，在弱磁区控制电流矢量沿着电流极限圆逆时针向下旋转，如图1中AC段.

图1 IPMSM运行过程定子电流轨迹Fig.1 Trajectory of stator current for IPMSM

图2为传统直流侧电压环弱磁控制系统框图[2].当参考电压us＊大于usmax时，弱磁控制器通过PI调节器来产生去磁电流进行弱磁升速.这种弱磁控制方法效果良好，在实际应用中比较常见.然而，若给定电压usmax设定为udc／，则此过程中实际输出最大电压矢量轨迹半径为udc／的内切圆，而逆变器所能输出给电机的极限电压为正六边形边界，如图3（a）所示，此时，正六边形与内切圆之间的部分电压没有进行电流控制，即逆变器直流侧母线电压没有完全被利用，弱磁区转矩性能没有最大程度输出.若usmax增加至2udc／π，给定电压超出了正六边形，而实际电压不可能达到超出正六边形的部分区域，此时系统中可能会产生大量谐波甚至系统不稳定[4，7].为此，本文提出一种新的弱磁算法在实现弱磁扩速的同时改善上述弱磁过程中的转矩性能.

图2 传统直流侧电压环弱磁系统框图Fig.2 Conventional field－weakening control system for IPMSM

2 弱磁控制策略

2.1 SVPWM 调制

SVPWM原理是逆变器通过6个基本电压矢量的组合，使输出的电压空间矢量轨迹接近电机的实际圆形旋转磁场.

电机在基速以下运行时，参考电压u＊s较小，处于正六边形内，调制前的参考电压u＊s与调制后实际输出电压us相等，两者电压差为零.随着转速升高，电机端电压达到逆变器输出的饱和极限电压，此时参考电压u＊s会超出正六边形边界，调制后输出的实际电压us会小于调制前的参考电压u＊s，即两者出现差值Δus，如图3（b）所示 .同时采用最小幅值误差过调制[8]的方法来调整参考电压使其落在正六边形内来跟踪实际电压轨迹.基于以上原理可知，电机端电压是否达到逆变器所能输出的极限电压，即是否开始进入弱磁区域可通过SVPWM调制前后的电压差来确定.同时用此电压差值来调节定子电流进行弱磁扩速，其实际输出的最大电压矢量轨迹会落在正六边形上，直流母线电压能得到更有效的利用，使得电机在弱磁区输出更大的电磁转矩.

图3 SVPWM电压极限与调制方法Fig.3 SVPWM limits and methods

2.2 恒转矩MTPA运行分析

IPMSM的电磁转矩方程为：

为充分利用定子电流，在恒转矩区域采用MTPA控制，其电流轨迹方程如下[6]：

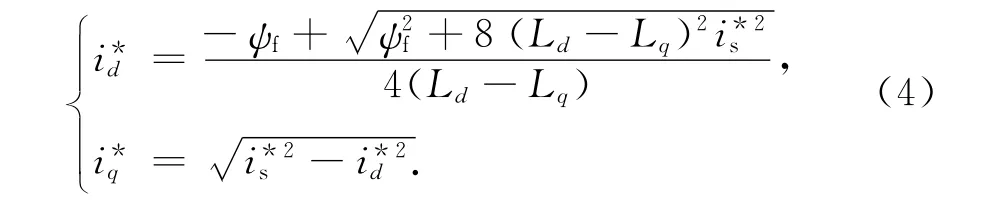
2.3 弱磁运行分析

高速时忽略定子电阻压降，电流调节器输出的参考电压与SVPWM调制后输出的实际电压之间的差值在d，q轴坐标系下可分别表示为[7]：

定义电压差值的代价函数为：

为了最有效地利用逆变器的直流母线电压，以参考电压与实际电压的差值F最小原则来分配弱磁区域内d，q轴给定电流分量的大小.运用梯度下降法原理[9]使得目标函数F的值最小，其表达式为：

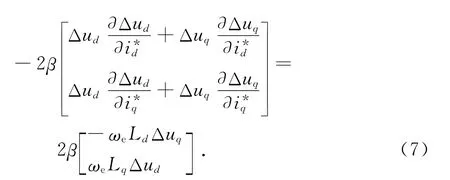
将式（7）等式两边积分可得：

式中：i＊d，i＊q为恒转矩区域的参考电流；i＊dm，i＊qm为弱磁区域重新分配的参考电流；β为大于零的常数.

从式（8）可以看出，若Δuq或Δud变为零，由于积分作用，i＊dm，i＊qm不能恢复为i＊d，i＊q，可用低通滤波器来代替这里的积分器.则表达式为：

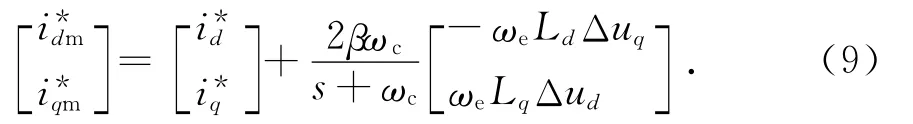
式中：ωc为低通滤波器截止频率.

电机在运行过程中定子电流矢量在d，q轴上的电流分量始终满足以下关系式：

从图1中的定子电流矢量轨迹可知，弱磁运行过程中定子电流矢量在d，q轴平面上沿电流极限圆逆时针旋转角度Δθ，有

式中：θ为电流相位角；Δθ为定子电流弱磁角.结合式（9）和式（10）可得：

电机弱磁运行时工作于图1中第二或第三象限，Δθ在[－π／2，π／2]内变化，由式（12）可见，此时弱磁角Δθ与等式右边变量T成线性变化，又因控制系统具有自调节能力，故可通过控制变量T来直接控制弱磁角Δθ.于是，弱磁角的等效表达式为：

式中：ρ＝Lq／Ld.当电机处于电动运行状态时，工作于图1中第二象限，α为大于零的常数；当电机处于发电运行状态时，工作于第三象限，α为小于零的常数.本文以电机工作于第二象限为例来讨论其弱磁运行过程，后文对此不再另作说明.

弱磁控制算法框图如图4所示.基速以下，电机端电压未达到逆变器输出的最大电压，SVPWM调制前后的输出电压相等，弱磁角Δθ输出为零，此过程采用MTPA控制获得最大电磁转矩.随着转速继续上升，实际输出电压达到饱和时，参考电压与实际电压之间出现电压差值，弱磁控制器输出弱磁角来改变参考电流i＊d与i＊q.转速进一步上升至给定转速，系统稳定运行.

图4 弱磁控制算法框图Fig.4 Proposed field－weakening control strategy for IPMSM

3 仿真与实验结果

3.1 仿真结果及分析

运用Matlab／Simulink工具箱建立仿真模型，验证本文所述弱磁控制算法的正确性.IPMSM电机参 数 为：PN＝6kW；nN＝2 000r／min；rs＝0.031 8Ω；Ld＝0.612mH；Lq＝1.29mH；Ψf＝0.063 3Wb；np＝6.一阶低通滤波器的截止频率设置为200Hz，参数α设置为5.

图5为电机带10N·m负载启动弱磁扩速至6 000r／min的系统仿真变化曲线.从图5可以看出，在0.1s前，弱磁环输出为零，定子矢量角θ恒定，id和iq基本保持恒定，电机运行于 MTPA曲线上.电机进入弱磁区域时，弱磁角Δθ开始输出正值，电流矢量沿图1中曲线AB逆时针旋转，θ逐渐增大，从而id逐渐减小，iq逐渐增大.图5（c）可知，系统稳定前，定子电流幅值i＊s保持最大输出70A，额定转速以下，电机保持最大转矩运行，弱磁运行时转矩随电流变化而逐渐下降.整个过渡过程，电流变化快速而平稳，达到稳定时系统各变量无超调地跟随负载变化.

3.2 实验结果及分析

建立实验系统对本文所提算法进行实验验证.系统采用TI公司的DSP芯片TMS320F2812作为主控器件，PWM载波周期为7.5kHz，直流母线电压为150V，实验电机参数与仿真模型参数相同.

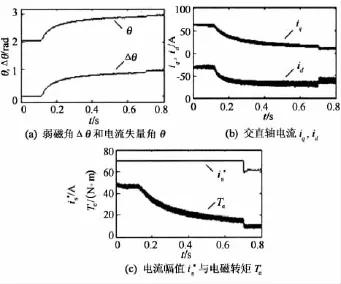
图5 弱磁控制过程仿真波形Fig.5 Simulation results operating on the proposed field－weakening control method

图6为整个弱磁控制过程各变量实验变化波形.在图6（a）和图6（b）中，d，q轴电流在恒转矩区域保持恒定，电流矢量角θ输出恒定值约为113°，弱磁角无输出.电机转速上升超过额定转速后，弱磁角逐渐增大，高速时弱磁角变化较为缓慢，达到6 000 r／min时约为165°，电机还可以弱磁运行于更高的转速.d，q轴电流在弱磁区域根据电流矢量角的变化而重新分配，可以看出id与iq运行轨迹平整无振荡且快速恢复至稳态值 .由图6（c）可知，电机在转速达到2 200r／min后，电磁转矩才开始明显下降，电磁转矩从恒转矩到弱磁过程过渡平滑.电机带载启动到稳定于6 000r／min约为2.5s，响应速度快.

图7为使用本文方法与图2中传统直流侧电压环弱磁方法的实验对比图，包括电磁转矩与转速关系曲线以及电流相位角与转速关系曲线.从图7（a）可以看出，在弱磁区域电机运行于相同的转速，采用本文控制方法所产生的电磁转矩比采用传统弱磁方法要大.例如，在转速到达6 000r／min时，本文方法产生的转矩约为16N·m，传统弱磁方法产生的转矩约为14N·m，转矩幅度提高了约14%.由图7（b）可知，弱磁过程中达到同样的转速，相比于传统方法，本文提出弱磁方法电流相位角更小，因而进行重新分配的电流id，iq也相对更大 .这进一步说明本文提出的改进算法产生更高的转矩，更好地利用了直流母线电压.

图6 弱磁控制过程实验波形Fig.6 Experimental results operating on the proposed field－weakening control method

图7 本文方法与传统方法控制性能对比曲线Fig.7 Control performance comparison of proposed method and conventional method

4 结 论

本文提出了一种新的基于内置式永磁同步电机的弱磁控制策略.基于内置式永磁同步电机弱磁原理，分析了当系统进入弱磁区域时，SVPWM调制前输出的参考电压与调制后输出的极限电压两者之间会出现电压差，并将此差值作为弱磁控制器的输入量来改变定子电流相位角，从而重新分配交直轴电流的大小来实现弱磁扩速.仿真分析和实验结果表明，本文提出的弱磁控制算法实现了电机高倍扩速运行，弱磁过渡平滑、响应速度快，且由于在弱磁区域能更有效地利用直流母线电压，相比于传统弱磁算法，电机输出更大的电磁转矩，对于改善系统的弱磁性能具有一定的实际意义和应用价值.

[1] VERL A，BODSON M.Torque maximization for permanent magnet synchronous motors[J].IEEE Transactions on Control System Technology，1998，6（6）：740－745.

[2] KIM J M，SUL S K.Speed control of interior permanent magnet synchronous motor drive for the flux weakening operation[J].IEEE Transactions on Industry Applications，1997，33（1）：43－48.

[3] BAE B H，SUL S K.New field weakening technique for high saliency interior permanent magnet motor[C]／／Proceedings of the Thirty－eighth IAS Annual Meeting on Industry Applications.New York：IEEE，2003：898－905.

[4] 吴芳，万山明.一种过调制算法及其在永磁同步电动机弱磁控制中的应用[J].电工技术学报，2010，25（1）：58－63.WU Fang，WANG Shan－ming.An overmodulation algorithm and its application in PMSM drive with flux－weakening control[J].Transactions of China Electrotechnical Society，2010，25（1）：58－63.（In Chinese）

[5] 赵云，李叶松.永磁同步电机宽范围最大转矩控制[J].电工技术学报，2010，25（7）：45－50.ZHAO Yun，LI Ye－song.Maximum torque control of surface mounted permanent magnet synchronous motors in wide speed range[J].Transactions of China Electrotechnical Society，2010，25（7）：45－50.（In Chinese）

[6] 唐任远.现代永磁电机理论与设计[M].北京：机械工业出版社，2006：259.TANG Ren－yuan.Modern permanent magnet machines theory and design[M].Beijing：Machines Press，2006：259.（In Chinese）

[7] KWON T S，SUL S K.Novel antiwindup of a current regulator of a surface－mounted permanent－magnet motor for fluxweakening control[J].IEEE Transactions on Industry Applications，2006，42（5）：1293－1300.

[8] BRIZ F，DIEZ A，DEGNER M W，etal.Current and flux regulation in field－weakening operation[J].IEEE Transactions on Industry Applications，2001，37（1）：42－50.

[9] IOANNOU P A，SUN J.Robust adaptive control[M].Upper Saddle River，NJ USA：Prentice－Hall，1996：785－786.