应用神经网络的变流器波形复合控制策略＊

戴瑜兴，陈义财，全惠敏，郜克存，曾国强

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.95918部队，湖北 随州 432701；3.温州大学 物理与电子信息工程学院，浙江 温州 325035；4.青岛创统科技发展有限公司，山东 青岛 266012）

岸电电源是供电停港船舶的港口岸上电源，可代替停港船舶的主辅燃油发电机供电，是控制港区空气质量日益恶化的重要方式.PWM可逆变流器是岸电电站的核心研究对象，与传统变流技术相比，具有高功率因素和低谐波污染的优点，在岸电电源、UPS、军用设备、太阳能和风能等清洁能源使用中得到广泛的应用.

港口现有岸电变流器多使用PID控制、内模控制、无差拍控制和重复控制等方式，无法同时满足大功率、强冲击、高稳定的供电需求而未得到广泛使用[1].PID控制虽鲁棒性较强，但在非线性负载、噪声或扰动影响下，设定的控制参数无法得到稳定和精确的控制效果.内模控制虽参数简明，动态响应较好并有较强的鲁棒性和抗干扰性，但难于建立精准模型.无差拍控制静态输出稳定及动态反应较快，但易出现较强振荡，鲁棒性较差.重复控制较大改进了电源变流器的稳定输出，但因有一个周期的控制延迟影响了动态响应效果.神经内模控制在有精确模型的基础上可确保系统有很好的鲁棒性和动态性能，但因其需要在线训练学习才能获得精确模型，致使算法还未获得大量应用[2－6].目前，各种输出高精稳定且抗扰性强的智能控制策略成为高性能变流器的研究热点.

针对两电平三相PWM可逆变流器在DQ坐标系下的特点，本文利用改进的重复控制策略与神经网络内模控制策略相结合，设计了变流器输出波形复合控制器，并通过实验测试了该控制策略性能.

1 变流器拓扑结构及模型解耦

两电平三相PWM可逆变流器拓扑结构如图1所示.该结构共分为网侧滤波单元、电压型PWM整流单元、直流储能单元、电压型PWM逆变单元与负载侧滤波单元等5个部分.

图1 岸电电源PWM可逆变流器拓扑结构图Fig.1 PWM shore power converter topology

定义Sk＝1（k＝A，B，C，U，V，W）时拓扑结构中桥臂上管导通，下管关断；Sk＝0（k＝A，B，C，U，V，W）时拓扑结构中下管导通，上管关断.如图1所示，依据KCL和KVL定律，得在三相静止坐标系下整流回路方程为：

式中：eAG，eBG，eCG分别为三相电压输出大小；vdc为整流输出电势；vNG为中线点电势差，iA，iB，iC分别为三相输出电流大小；R1和L1分别为输入端滤波电阻和电感大小；C为储能电容值.将三相静止坐标系分别经Clark变换和Park变换到两相旋转DQ坐标系.可得变换矩阵为：

利用式（2）变换矩阵将式（1）参量进行DQ坐标变换，整理可得PWM整流单元回路在DQ坐标系下数学模型为：

式中：各变量为三相坐标系下经Park变换后得到的DQ坐标系下对应变量.由式（3）可知，整流回路参数经两相坐标变换已呈线性化.定义id＊，iq＊为id，iq电流的指令值；Kip为电流内环比例调节增益；KiI为电流内环积分调节增益.采用前馈PI控制策略将d轴和q轴变量解耦可得：

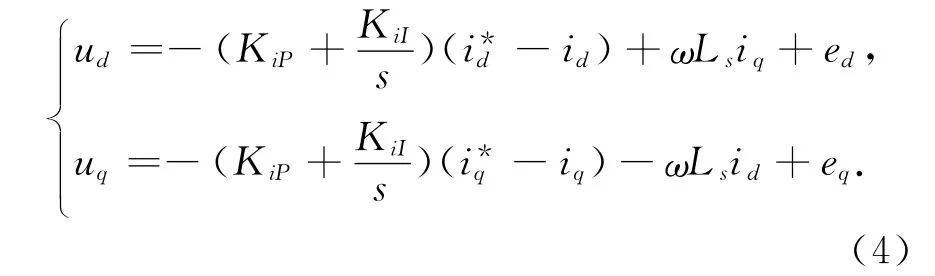
将式（4）带入式（3）可得电流控制输入为：

同理得图1中逆变回路方程为：

式中：k＝U，V，W和uok为输出相电压，ik为输出相电流，R2和L2分别为输出端滤波电阻和电感大小，Co和RC为输出滤波电容容值和阻值大小.将式（6）控制量经Clark坐标变换解耦可得控制输出为

式中：uoα，uoβ，iα和iβ为PWM 逆变桥输出三相电压电流经Clark变换对应变量.由式（5）和式（7）可知，经过两相旋转坐标变换及解耦，在DQ坐标系下各输入或输出控制量间没有耦合关系并相互独立，可以分别控制两相坐标系下变量实现对整个变流器的控制.

2 重复控制单元控制器设计

重复控制理论是建立在内模控制的基础上，其核心在于内部模型设计[1].在常用重复控制策略模型应用中普遍存在两个方面不足.一是由于延时单元z－N的存在，使得系统动态性能较差，对扰动调节时间超过了一个周期.二是因滤波器Q（z）的使用，使得系统增强稳定性的同时存在了静差.

图2为针对这两个问题对内模改进的一种重复控制策略.如图2所示，重复控制器由滤波单元Q（z）z－N，内模N阶周期延时单元z－N，补偿器C（z）3部分组成.

图2 重复控制单元结构图Fig.2 The repetitive control unit structure diagram

滤波单元Q（z）z－N＝1时，系统理论上可以实现无静差，但是这种纯积分控制结构使系统稳定性和鲁棒性变得很差，在工程实际应用中是被禁止的.因此为改善系统稳定性，一般使辅助补偿器Q（z）为低通滤波形式或者为略小于1的常数，如0.95.

延时单元z－N是内模组成部分，当控制信号检测到误差信息时使延时至下一个周期动作.z－N的存在虽然影响了系统动态性能却是重复控制内模的固有组成部分，不能舍弃[7].因指令和扰动在很多情形下都重复出现，如图2所示，经改进的嵌入式结构使系统保留了指令信号的快速响应通道.

补偿器C（z）将获得的系统补偿量在下一周期作用于控制对象校正输出.取C（z）＝KrzkS（z），该设计可保证系统运行稳定性并改善修正效果，超强补偿相位幅值.其中Kr为重复控制幅值增益补偿；zk为相位补偿；S（z）起滤波作用消除谐振峰值、校正中低频增益并增强高频衰减特性.S（z）的存在虽然使zk的相位补偿相对滞后，却增强了系统的高频抗干扰能力和系统稳定性.

3 神经网络内模控制单元设计

神经内模控制器设计如图3所示，分别用神经网络控制器 NNC（neural network controller）和神经网络预估模型 NNM（neural network model）取代内模控制结构中的被控对象预估模型和内模控制器.由内模原理可知，只要NNM和NNC稳定则系统稳定，即当NNC为NNM的逆时，系统误差e（k）＝y（k）－r（k）＝0[8].

图3 神经内模控制器结构图Fig.3 Neural internal model controller structure diagram

3.1 神经网络预估模型NNM设计

采用经典的前向BP神经网络设计NNM神经网络预估模型.如图4所示.定义xj（k）为输入层输入；netj（k）和zj（k）为隐层输入和输出；rm（k）为输出层输出；ym（k）为网络输出；θi为输入层阀值；wij，vi为BP网络结构层间网络权值.

图4 BP神经网络结构Fig.4 The structure of BP neural network

由图5知，输入层输入xj（k）为：

则知netj（k），zj（k），rm（k）为：

NNM性能指标为：

定义δi（2）（k）为隐层误差，δ（3）（k）为输出层误差，则有：

BP网络结构层间在以学习速率为ηm，动量因子为αm时，其网络权值wij，vi和输入层阈值修正θi为：

3.2 神经网络控制器NNC设计

根据内模原理稳定性充分条件，控制器NNC设计结构应是预估模型NNM结构的逆，故NNC应采用与NNM同样的三层BP神经网络结构设计.由图4知，NNC结构比NNM多一个输入层网络节点f（k）.定义cj（k）为输入层输入，bj（k）和gj（k）为隐层输入和输出，tij，hi为BP网络结构层间网络权值.则由图5可得NNC输入层输入xj（k）为：

NNC结构中隐层输入bj（k）、隐层输出gj（k）、网络输出rm（k）为：

NNM性能指标为：

为保证控制器精度不随预估模型精度变化，式（18）中，ec（k）＝r（k）－y（k），y（k）不能用ym（k）代替.当NNC在以动量因子为αc，学习速率为ηc时，其网络权值tij，hi为：

当对象为非线性或时变性时，利用BP网络能经过一定次数的学习逼近非线性映射的特点，ym（k）能够无限逼近y（k），此时则可用∂ym／u替代∂y／u.

由式（12）可得：

定义δi（1）（k）＝δ（2）（k）hi（k）gi（k）（1－gi（k）），δ（2）（k）＝r（k）－y（k），则：

同理可得：

将式（21），式（22）代入式（19）可得权值和阈值调整公式：

3.3 神经网络内模控制器设计

通过对PWM变流器回路方程坐标变换并解耦后，变流器d／q轴z域传递函数模型可表示为：

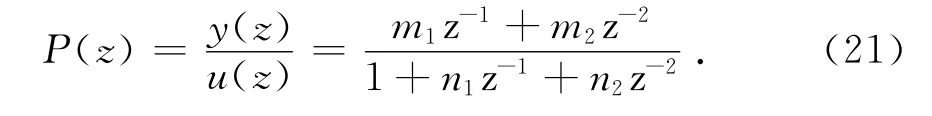
则有：

即：

由式（26）可知，设计NNM中BP神经网络结构各层神经元数分别为4－4－1，则输入层输入为[u（k－1），u（k），y（k－1），y（k）]T，计算性能指标函数得Em＝（y（k）－ym（k））2／2.同理可知，NNC中BP神经网络结构应设计为各层神经元数分别为5－4－1，且输入层输入为[r（k－1），r（k），u（k－1），u（k），f（s）]T，计算性能指标函数得Ec＝（r（k）－y（k））2／2.

4 复合控制器设计及实验验证

复合控制器结构框图设计如图5所示.通过改进的重复控制单元和神经网络内模控制单元共同作用于可逆变流器中电流输入和电压输出.该控制方案中，重复控制单元通过改进可保证在稳态时输出高精度的稳态波形，能够适用于船舶各精密仪器用电需求，但一旦有给定指令，重复控制器需延时至下一个周期作用被控制对象.神经内模控制单元控制无静差，动态响应快，在重复控制的延时周期能快速动态响应指令，很好的填补了重复控制单元的不足，但神经网络内模控制单元中NNM预估模型需要在线训练学习才能获得精确模型.因此神经网络内模控制与重复控制单元综合的波形复合控制器使系统的负载适应性和鲁棒性得到增强，强有效地改善了可逆变流器的输出波形.

图5 复合控制器结构图Fig.5 Composite structure diagram of the controller

搭建如图6所示实验平台验证该波形复合控制策略，以TI公司生产的时钟频率达150MHz的TMS320F28335为DSP控制芯片，辅以各采样电路、驱动电路及保护电路等.用泰克TDS3032示波器和电能质量分析仪Fluke43B做为测试工具，采用表1中参数验证可逆变流器波形复合控制器的实际控制效果.

图6 实验平台搭建结构图Fig.6 Structure diagram of experimental platform

4.1 稳态性能

通过搭建的实验平台分别测试PWM整流器和PWM逆变器稳态性能.图7（a）为电能质量分析仪对PWM整流器稳态时输入A相的功率因数测试结果，表明整流网侧功率因数高达0.99.图7（b）为PWM整流器输出直流电压波形和A相输入电流波形测试结果表明输出电压稳定在600V±2%，A相波形失真率为1.9%.可见PWM整流器功率因数高，对电网无谐波污染.

表1 PWM可逆变流器实验平台设置参数Tab.1 Converter experiment platform parameters

图7 PWM整流器稳态功率因数和输出波形Fig.7 PWM inverter load waveform test

图8为PWM逆变器供电纯阻性负载和混合负载稳态输出波形测试结果，表明波形质量好，稳定精度高，谐波总失真度 THD（Total Harmonic Distortion）供电纯阻性负载时为1.04%，供电非线性混合负载时为1.4%，均达到满意效果.

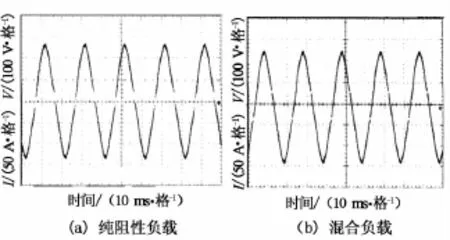
图8 PWM逆变器负载波形测试Fig.8 PWM inverter output waveform comparison

图9为采用复合控制与采用PI控制PWM逆变器稳态输出波形比较测试结果，表明采用复合控制波形明显好于PI控制波形.

图9 PWM逆变器稳态输出波形比较Fig.9 The dynamic performance test of PWM inverter

4.2 动态响应

采用负载突然增加或减少来验证该复合控制器的动态响应性能.图10为变流器负载突变时PWM逆变器波形测试结果.由输出波形可知变流器均在负载突变的第一个周期迅速响应，在两个周期内输出均稳定下来，证明采用复合控制器的变流器具有良好的动态响应性能.

图10 PWM逆变器动态性能测试Fig.10 PWM inverter output waveform comparison

图11为采用复合控制与采用PI控制PWM逆变器动态输出波形比较测试结果，显示突加负载时采用复合控制的输出波形在突变周期的顶部稍有失真，随后没有明显的变化.采用PI控制的输出波形则有严重的失真，随后波形有幅值变化.显然采用复合控制的波形明显好于PI控制波形.

图11 PWM逆变器动态输出波形比较Fig.11 PWM inverter output waveform comparison

4.3 鲁棒性和扰抗性

通过调节实验平台PWM整流部分输出的直流电压大小，测试PWM逆变部分输出电压的波动大小，分析该系统的鲁棒性和扰抗性.测试数据如表2所示，逆变部分在直流母线波动的状况下，输出始终稳定.其中相电压误差始终稳定在2%以内，THD值在1.8%以内，输出频率稳定.

表2 整流输出电压变化时变流器输出数据测试Tab.2 Rectifier output voltage changes the output data test

5 结 语

分析了港口现有岸电电源产品所采用控制策略的不足，研究了岸电电源中PWM可逆变流器的数学模型在DQ坐标系下的特点，提出了一种基于改进的重复控制和神经网络内模控制的波形复合控制策略，该策略能够很好的综合两种控制策略的优势，互补不足.通过搭建实验平台验证该控制策略，实验证明，应用该复合控制策略的PWM可逆变流器波形输出稳定，精度高，THD值低，负载适应性强，动态响应快，符合船级社的船舶用电标准，可以在岸电电源应用中推广使用.

[1] 杨金辉.数字化PWM逆变系统控制关键技术研究及其应用[D].长沙：湖南大学电气与信息工程，2010.YANG Jin－hui.Digital PWM inverter system control key technologies and its applications study[D].Changsha：College of Electrical and Information Engineering，Hunan University，2010.（In Chinese）

[2] KHERSONSKY Y，ISLAM M，PETERSON K.Challenges of connecting shipboard marine systems to medium voltage shoreside electrical power[J].IEEE Transactions on Industry Applications，2007，43（3）.

[3] 李士勇.模糊控制·神经控制和智能控制论[M].哈尔滨：哈尔滨工业大学出版社，1998：91－101.LI Shi－yong.Fuzzy control·neurocontrol and intelligent cybernetics[M].Harbin：Harbin Institute of Technology Press，1998：91－101.（In Chinese）

[4] SHIGEMATSU J，SUDUO S，SHI A.Present conditions and future trends for AMP[J].Shikawajima Harima Engineering Review，2006，46（4）：156－160.

[5] 郜克存，戴瑜兴，杨金辉，等.三相高功率因数整流器的神经网络内模控制[J].电机与控制学报，2012，16（2）：44－49.GAO Ke－cun，DAI Yu－xing，YANG Jin－hui，etal.The control method of three－phase rectifier based on neural network internal model theory[J].Electric Machines and Control，2012，16（2）：44－49.（In Chinese）

[6] SHIGEMATSU J，SUDOU S，SHI A.Present conditions and future trends for shikawajima[J].Harima Engineering Review，2006，46（4）：156－160.

[7] KEVIN L P，PCNIAMIN B C，MOHAMMEDL，etal.Tackling ship pollution from shore side[J].IEEE Industry Applications Magazine，2009，Jan－Feb：56－60.

[8] 赵耀.内模控制系统鲁棒跟踪控制器的参数化及优化[J].控制与决策，2009，24（5）：734－737.ZHAO Yao.Parameterization and optimization of robust tracking controllers for internal model control[J].Control and Decision，2009，24（5）：734－737.（In Chinese）