基于任务可靠性的使用保障设备优化配置模型
2013-08-14盛旺齐建军黄生俊郭波
盛旺,齐建军,黄生俊,郭波
(国防科学技术大学信息系统与管理学院,湖南 长沙 410073)
0 引言
随着现代军事的深入变革,以及科学技术的快速发展,武器装备的使用保障能力显得越来越重要。在有限时间的条件下满足武器装备作战能力的要求是当前使用保障的关注点之一,因此,对使用保障资源配置问题的研究,是武器装备发展的必然趋势。
基本作战单元是指按照部队建制由相同主战装备及其附属保障系统构成可独立执行作战或训练任务的军事单位[1]。对其进行使用保障作业,是为保证装备正确动用以便能充分发挥规定的作战性能所进行的一系列技术与管理活动[2]。使用保障设备配置方案的合理与否直接关系到基本作战单元总体效能的优劣,但是当前相关研究与实际情况联系不够紧密,不能很好地将研究成果转化为实际应用。
国外将维修保障和使用保障结合进行研究,国内主要对使用保障费用、使用保障资源和使用保障能力等方面进行研究。例如:Gainen[3]等主要研究在一定费用的情况下,通过仿真的方法协调飞机数量、维修人员数量、维修设施数量和备件数量以保证飞机中队最大限度地安排飞机完成任务;Li.Li[4]等人研究了以最小化完工时间为目标的任务时间不确定的鲁棒性资源配置问题;吕卫民[5]提出了某型导弹装备的使用保障能力评估指标体系,运用模糊理论建立了多级模糊层次综合评判模型,给出了导弹装备使用保障能力的量化评估方法。国内外的研究侧重于对时间、资源的优化以达到费用最小化,从而求得最合理的配置方案,但是与实际问题的联系不够紧密,不能很好地解决实际存在的问题。
根据对实际情况的分析,基本作战单元的保障工作,是在完成作战任务之后,成批进行保障工作且数量确定,保障设备需要对相关装备进行保障作业,主要是在规定的时间内对保障资源的优化,即在规定的时间内,达到满意的保障资源配置要求即可,不要求一定要达到最优。一般来说,会有多个保障设备对所有的主战装备进行保障,但是,由于费用、时间等因素的影响,很少会有一对一保障,这就造成了当保障设备工作时有主战装备在等待服务,与排队论相关理论类似,所不同的是本文研究的输入过程为确定型数值,即非动态随机过程。
排队论是运筹学的一个分支,又被称为随机服务系统理论或等待线理论,是研究要求获得某种服务的对象所产生的随机性聚散现象的理论[7]。当前排队论的研究对于求瞬态解的研究并不多。叶梧[8]等把福克-普朗克方程降阶去奇异性,转化为有外力作用的状态方程,利用Runge-Kutta法,求得系统的瞬态及稳态解,并给出不同参数时的曲线族。而运用排队论的理论和方法对资源优化配置的研究则相对较多。Gransberg,Douglas D.等(1998)和Garrido,Rodrigo A.等在集装箱港口设备配置研究中(2000)采用排队理论建模,前者讨论了以船舶等待时间最小为目标的合理设备配量问题,后者估算了码头的效率及其影响因素[9]。陈永龙[10]等通过对使用保障资源和工作的分析,利用相似系统法确定人力与人员的需求,用排队论确定保障设备的数量。
相关研究无论是求瞬态解还是稳态解,都建立在输入过程和服务过程是随机的且两者动态交互的基础上,其理论和方法对本文输入确定的非动态交互条件下,规定时间内的保障设备配置问题不具备直接求解的能力。本文对基本作战单元的使用保障设备配置问题进行描述,以任务可靠度为比较依据,分别构建了单保障设备和多保障设备两种保障方案评估模型,通过对使用保障方案的评估来确定使用保障方案是否能达到规定的任务可靠度。并采用解析方法对两个模型进行求解,最后给出评估实例并进行了仿真验证。
1 模型构建
1.1 问题描述
基本作战单元包括主战装备和保障资源,其任务可靠性是指装备在规定的任务剖面中完成规定功能的能力,本文中用任务可靠度来衡量。由于作战环境、作战以及敌方袭击时间间隔的限制,基本作战单元的使用保障工作必须在规定的时间内完成(本文取时间上限为D)。我们假设基本作战单元在完成一次作战任务时,需要对所有的主战装备进行保障任务。实际的调研结果显示,在对基本作战单元进行保障时,保障作业的流程固定,对于保障设备而言,只有在上一个装备的保障作业完成后,才能对下一个装备进行保障作业,并且需要在规定的时间内完成对所有装备的保障任务,以任务可靠度来进行衡量。这时,对于保障任务来说,所有的主战装备同时到达保障设备所在的地点,也就是说输入过程是成批到达。一般来说,保障设备的服务时间是随机的,我们总假定服务时间的分布是平稳的,即分布的期望值、方差等参数不受时间的影响,且每一台装备接受服务是相互独立的,对下一装备接受保障任务没有影响,具备无后效性。因此,设每个保障设备的服务时间服从负指数分布。
由于使用保障设备的配置是个比较复杂的问题,为方便问题的描述和求解,我们将使用保障系统的复杂性和作业的多样性进行简化,仅以一个保障作业作为研究的对象。当主战装备一次任务完成后,主战装备经过该保障作业即完成了保障任务,具备进行下一轮作战任务的运动能力。该保障作业对保障设备的数量要求假定一个简单的配置方案,我们需要对该配置方案进行时间评估,以确定该方案是否能在规定的时间内,达到所要求的任务可靠度,从而对配置方案进行评估或者修改。
同时,为了便于对问题的理解,我们通过构建单作业单保障设备模型到构建单作业多保障设备模型来对问题进行分析和建模,并运用仿真方法进行验证。
1.2 单个保障设备模型
单个保障设备就是只有一个服务设备来对顾客进行服务。这里的顾客即是需要进行保障作业的主战装备。通过该设备,即完成了主战装备保障作业。
本文所构建的单个保障设备模型满足以下条件:
a)输入过程
顾客源是完成作战任务的装备,其数量有限且成批到达,相互独立。
b)排队规则
单队列,队长为装备的数量,队列排序随机。
c)服务机构
单个保障设备,服从参数为μ的负指数分布,对各个顾客的服务是相互独立的。
此外,根据实际情况,对于基本作战单元来说,需要保障的装备成批到达后,该单位一般不会再有另一批相同的装备到达,即主战装备只有一批,且数量确定。在进行保障作业时,只有在一台装备完成保障作业后,下一台装备才能进入保障设备接受保障作业,假设主战装备接受服务是连续的,没有时间间隔。
单保障设备的基本模型如图1所示。
设需要接受保障作业的主战装备数量为K,保障设备的服务时间服从参数为μ的负指数分布,即服务时间T的概率密度函数为:


图1 单保障设备排队系统
保障作业完成的任务可靠度要求为Psat。假设保障作业保障设备不发生故障,能够持续工作。
设ti为对装备i的保障作业时间,ti(i=1,2,…,K)相互独立,完成所有保障作业的时间为我们可以推导出总时间TK的密度函数,即完成所有保障作业的总时间TK的密度函数为[11]:

因为当 n=1 时,fT1(T1)=μ·exp(-μT1),成立;设当n≤m时,成立。则当n=m+1时,令Tm+1=Tm+tm+1,因为Tm和tm+1相互独立,所以根据卷积公式可得:
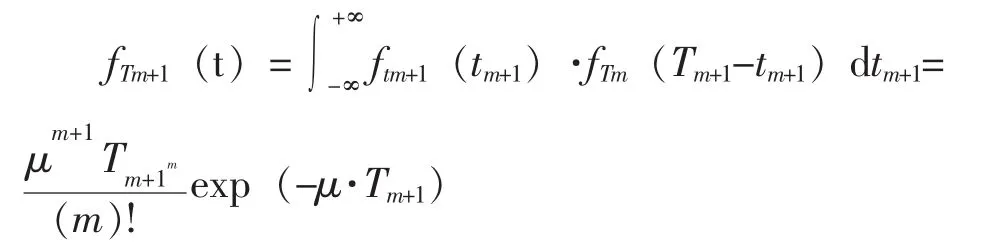
左右两边相等,即(2)式成立,所以总时间TK的密度函数即为(2)式。
在单个保障设备情况下,由于存在一个任务可靠度要求,所以我们要满足

因为

且

从而可以得到

将结果和任务可靠度要求Psat进行比较,如果不能满足,我们则需要增加保障设备,从而进入多保障设备模型。
1.3 多保障设备模型
一般来说,仅使用一个保障设备很难比较满意地完成任务,因此,我们需要设置多个保障设备来对顾客进行服务。
多保障设备模型如图2所示:

图2 多保障设备排队系统
本文所构建的多保障设备排队系统满足以下条件:
a)输入过程
顾客是完成作战任务的主战装备,其数量有限,成批到达且只有一批,相互独立。
b)排队规则
单队列,队长为主战装备到达的数量,队列排序随机。
c)服务机构
多保障设备,都服从参数为λ的负指数分布,且相互独立。
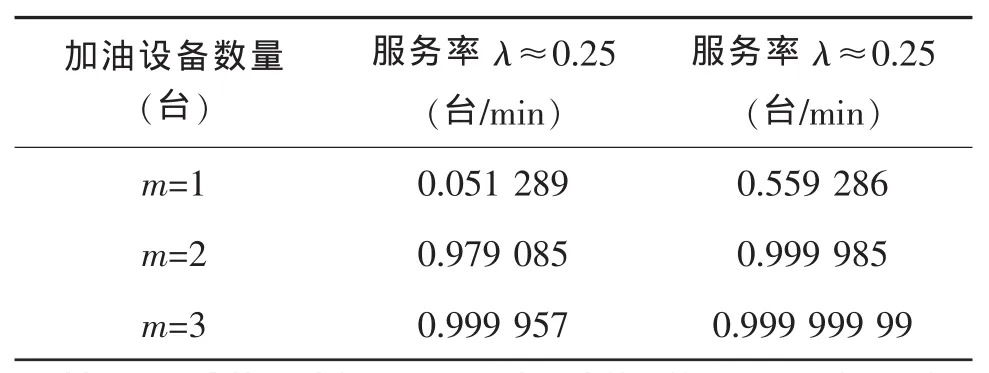
在构建多保障设备排队系统之前,我们需要先确定保障设备的初始数量。在此,我们设初始保障设备的数量为因为在实际中,出于经济的考虑,不会配备过多的保障设备,造成资源的浪费,所以,在多保障设备的排队系统中,1 当K=m时,即单队列中没有等待服务的装备,所有的保障设备参与服务。此时,工作时间最长的保障设备,其服务时间就是整个排队系统的工作时间。令Ti,i=1,…,K为第i个装备接受服务的时间,排队系统的总服务时间为Ts,则Ts=max(T1,T2,…,TK)。所以总服务时间的概率分布函数为: 证明如下: 当n=2时,因为T1,T2相互独立,max(T1,T2)不大于Ts就等价于T1,T2都不大于Ts。所以 设当n=m时,式(6)成立,则当n=m+1时,令 M=max(T1,T2,…,Tm),M′=max(M,Tm+1)则 得证。 因为保障设备的服务时间T服从参数为λ的负指数分布,所以每个保障设备的分布函数为FT(t)=1-exp(-λt),所以,总服务时间的分布函数为: 对分布函数求导,即可得到服务总时间的密度函数为: 当K>m时,即单队列中存在K-m个装备等待服务。m个保障设备同时工作时,当其中一个保障设备对一个装备完成保障作业时,等待保障的装备就逐个地进入保障设备中接受服务,直到K-m个装备全部进入保障设备中接受服务。当队列中最后一个等待保障的装备进入保障设备时,没有后续装备在队列中等待,这就演化成了K=m时的情形, 令此时的服务时间为Tm,根据前文的介绍,在这种情况下,其密度函数为: 这里主要介绍K-m>0个装备在等待时的服务时间密度函数。在这种情况下,m个保障设备同时工作且队列中存在等待服务的装备,因此,与单保障设备排队系统类似,将m个保障设备看作一个整体,其服从参数为mλ的负指数分布,根据单保障设备排队系统的服务时间密度函数,我们可以得到在此情况下的密度函数为: 又因为Tm和TK-m相互独立,令Tz=TK-m+Tm,则根据联合概率的计算公式可得: 在得到多保障设备服务时间的概率密度函数后,我们需要把规定时间内的任务可靠度与任务可靠度要求Psat进行比较,即计算: 如果P(Tz≤D)小于Psat,则需要增加一个保障设备;如果P(Tz≤D)大于Psat,则减少一个保障设备,再与任务可靠度要求比较。利用边际分析法,当D)时,符合条件的最优保障设备数量就为m台。 加油作业对于基本作战单元而言,是一个必经的保障过程,当作战装备的油料储量低于警戒线时,就需要对装备进行加油作业,以保证装备能够持续地执行任务。现假设需要为某型装备加油,运用上述模型进行计算和结果分析。 假设某型装备配备了31台,每次作战任务完成后,平均加油时间为4 min,加油作业服务率为λ≈0.25台/min,服务时间服从负指数分布。设任务时间D=90 min,任务可靠度要求为Psat=0.98。我们设初始加油设备的数量]台,在该算例中,K=31台,因此,m=2台。通过仿真模型和解析模型计算以及与任务可靠度要求的比较,其中,与任务可靠度要求进行比较的是解析计算的任务可靠度,得出加油设备的合理配置数量,结果如表1所示。 表1 任务可靠度仿真模型与解析模型计算结果对比 从表1中可以看出,对于算例,配备3台加油设备能够在规定的时间内达到所要求的任务可靠度。 由于加油作业关系到作战装备能否快速地进入机动作战状态,因此,对于加油技术的改进也比较重要,在文中即是逐渐地增大。为了便于比较,我们在原有的技术基础上,假设加油技术得到改进,加油设备服务率增大,令服务率为λ=0.35台/min,再运用模型进行计算,并与服务率为λ≈0.25台/min的情况进行比较,结果如表2所示。 表2 不同加油作业服务率情况下的任务可靠度 从结果可以看出,当加油技术改进,加油服务率提升时,在规定的时间内完成任务的任务可靠度就会提升,对加油车的数量要求也会减少。可见,本文解析模型能够为使用保障设备的配置提供一定的参考。 基本作战单元的使用保障设备配置问题,是从作战需求出发,在满足作战任务的前提下,对使用保障设备进行合理的配置,对于军队建设和战斗力的提升,具有比较重要的经济意义和现实意义。 本文根据对实际情况的分析,结合基本作战单元作战任务的需求,构建了单作业模式下单保障设备和多保障设备排队系统模型,设计算例进行计算并运用仿真方法进行验证,较好地解决了实际的使用保障设备配置问题。 实际的使用保障问题更为复杂,涉及内容也更多,在本文的基础上进一步地探讨可修保障设备,多作业多保障设备的优化配置问题将是下一步研究的重点。 [1]郭霖瀚,康锐.基本作战单元任务持续性仿真度量模型研究[J].系统仿真学报,2009(1):325-329. [2]何成铭,孔繁柯,任双英.关于装备使用保障问题的探讨[J].装甲兵工程学院学报,2001(9):12-1. [3]CAINEN L,LEVINE R A,MCGLOTHLIN W H.A Base Logistics Management Game[R].U.S.Air Force Project RAND research memorandum,1958. [4]LI LI,XU CHANGQING,TAO MEIXIA.Resource allocation in open access OFDMA femtocell.Networks[J].Wireless Communications Letters,2012,1(6):625-628. [5]刘冬,丁光超,江式伟.某型导弹装备使用保障能力评估[J].火力与指挥控制,2010,35(3):68-71. [6]王兴贵,焦争昌.基于排队论的银行排队问题研究[J].湘潭师范学院学报,2008(30):58-60. [7]叶梧,苏文,黄廉辉.爱尔朗排队系统的瞬态分析[J].华南理工大学学报,1995,23(8):58-66. [8]董婧.基于WITNESS的集装箱码头串联排队网络系统资源配置研究[D].上海:上海交通大学,2006. [9]陈永龙,王玉泉,李世英.使用保障资源的确定方法探讨[J].装甲兵工程学院学报2003,17(3):59-62. [10]宋述龙.n个服从指数分布的独立随机变量和分布的推导[J].辽宁师范大学学报,1990(4):51-58.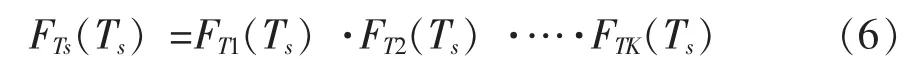








2 算例

3 结束语
