电器附件测试台运动系统的实现与分析
2013-08-14苏萌
苏萌
(工业和信息化部电子第五研究所,广东 广州 510610)
0 引言
电器附件作为介于电网和用电器具之间的一个重要支撑节点,安全取电的连接器件,其应用无处不在。电器附件测试台主要用于电器附件的检测,包括插头插座、家用开关和电器开关等。
在电器附件测试的往复运动过程中,不仅要有速度的变化控制,还要实现精确的定位控制。作为控制用的特种电机,步进电机[1]可以接收电脉冲信号并转化成与之相对应的角位移或直线位移,输入一个脉冲信号就得到一个规定的位置增量。步进电机的控制方式包括开环控制和闭环控制两种:开环控制方式的特点是控制简单、成本较低、实现容易,但是负载位置对控制电路没有反馈,在负载波动较大或速度较高的场合容易产生失步;闭环控制能直接或间接地检测出负载的位置和速度,实现很高的精度要求,但是成本上升较大,系统变得复杂,所以,现在步进电机的控制大多仍会采用开环控制方式[2]。
随着步进电机的广泛应用,对步进电机控制的研究也越来越多[3]。根据步进电机的频率转矩变化特性曲线,如果在电机启动停止或高速时步进脉冲变化太快,转子跟随不上电信号脉冲的变化就会产生失步或者过冲,因此,如何避免步进电机在高速转动或者急起急停时发生失步就成为在使用过程中的一个重要课题[4]。本文通过考虑测试台速度与负载的变化规律,拟合出线性规律与二次函数规律相结合的加减速曲线,避免了使用过程中步进电机常出现的失步问题,实现了测试台的高速运动。
1 测试台运动系统的理论建模
电器附件测试台是由步进电机带动丝杆传动机构转动,随着丝杆受到负载大小的变化,电机输出转矩也随之变化,在一定的速度下当需要输出的转矩大于步进电机的上限时就会发生丢歩或堵转[5]。
1.1 丝杆传动机构负载的分析
丝杆传动机构因其推力大、精度好和传动稳定的特点,广泛地应用在输出直线运动的场合,如图1所示,联轴器将步进电机与滚珠丝杆连接起来。要通过丝杆带动负载运动,电机输出的必需的负荷转矩为:

负荷的惯量:

式(1)、(2)中:VL——滑块运动的速度;
LB——丝杆的长度;
PB——联轴器的质量;
MC——联轴器的外径;
t1——移动时间;
M——滑动部分的质量;

图1 步进电机带动丝杆传动结构示意图
1.2 步进电机的矩频特性分析
步进电机的矩频特性可通过其动力学模型来描述:
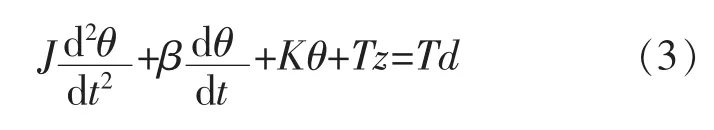
式(3)中:J——系统总转动惯量;
θ——转子转角;
β——阻尼系数;
K——与θ成某种函数关系的比例因子;
Tz——摩擦阻力矩及其他与β无关的阻力矩之和;
Td——步进电机所产生的电磁驱动转矩。
由式(3)可以看出,在升速阶段,角加速度应尽量地大一些,这样可以提高系统的快速性。如图2所示,步进电机的矩频特性使得电机起动时必须有一个逐渐升速的过程,停止时是由一个高速逐渐降速到零的过程。在起动或加速时如果升速太快,转子由于惯性而跟不上电信号的变化,就会产生堵转或失步;在停止或者减速时又会发生过冲。

从图2可以看出,步进电机的输出转矩随着频率的升高而急剧地下降,不是线性关系。步进电机经过的频率f1、f2、f3对应的输出转矩T1、T2、T3,频率变化量和输出转矩变化量分别为 Δf1、Δf2和ΔM1、ΔM2。由此得出:

为了符合步进电机的矩频特性,在步进电机进行降速时,应使频率的变化量逐次地递减,在加速时正好相反。
1.3 步进电机速度控制曲线数学模型
步进电机的输出力矩随着旋转角度的变化,角加速度也随着电机转子角速度的变化而变化,为使步进电机在不失步的条件下,以最短的时间内加(减)速到给定的速度,并且最大化地发挥步进电机的性能,如何建立合理的加减速控制曲线模型就成为控制的关键。
加减速控制规律一般有直线型和指数型两种选择,如图3所示。在直线型速度控制规律中,加速度是恒定的,快速性较好,控制简单,但是未充分考虑步进电机输出力矩随频率变化的特性,高速运动时可能会发生失步;并且在加减速和匀速之间不能光滑地过渡,存在阶跃现象,控制效果不理想。指数型控制规律虽然符合步进电机的矩频特性变化,在低频时加速度变化太小,而在高频时升速又太快。

图3 常见的步进电机加减速运行曲线
为了克服上述两种加减速运行曲线在实际控制过程中的缺点,本文将直线型和二次函数型两种加减速变化规律结合起来,如图4所示,这样既能实现步进电机快速升降速的特点,又能实现在加减速和匀速过程之间的平稳过渡,避免出现阶跃现象,最大化地发挥步进电机的性能。

图4 直线和指数相结合型加速度曲线
2 测试台运动模型分析
本文以插头插座寿命试验台为研究对象建立了实际模型,实际参数如表1所示。

表1 测试台运动机构参数
将表1的数据带入式(1)中得到电机必需的转矩:

由此选择leisai的57 HS 22-A作为测试台用的步进电机。
将上章建立的速度控制曲线分为两段,分别用方程表示。

对加减速过程曲线进行离散化分析,如图5所示,就得到单位时间间隔内要发送的脉冲数。对曲线函数进行积分,即得到各段曲线相对应的控制脉冲数。


图5 加速度控制曲线离散化

采用单片机不断地改变定时器值的大小来控制时钟脉冲的时间间隔,以拟合理想中的速度曲线,实践证明,测试台能在短时间内快速地升降速,运行平稳,定位准确,很好地实现了电器附件的测试要求。
3 结论
本文以电器附件测试台的运动机构为研究对象,建立了步进电机以及丝杆传动机构的理论运动特性模型,采用以直线控制和二次函数曲线控制相结合的加速度曲线,然后对建立的加速度曲线进行离散化处理,用单片机控制脉冲数的发送很好地拟合了速度控制曲线。
结果证明,采用此种方法能避免步进电机在高速运动以及带动大负载中常出现的丢歩及堵转问题,缩短了电机的加减速时间,最大化地发挥了步进电机的工作性能。
[1]李忠杰,万守信.步进电动机应用技术[M].北京:北京机械工业部出版社,1988.
[2]章小红,钱志良.步进电机控制系统的设计[J].苏州大学学报,2006(8): 42-44.
[3]毕绍新.步进电机驱动控制的应用研究[D].天津:天津大学,2003.
[4]ROBINSON D J,Dynamic analysis of magnetic step-ping motors[J] .IEEE Transon Industrial Electronics,1999,46(2): 370-379.
[5]荣盘祥,何志军.步进电机数字控制系统设计[J].电机与控制学报,2009,13(2): 272-275.
