基于蒙特卡罗的系统任务可靠性分析方法

刘钦文，赵品伦

（1.中国西南电子技术研究所，四川 成都 610036；2.成都军区空军司令部信息化处，四川 成都 610031）

0 引言

军用装备各项总体指标对确定和指导装备的工程设计起着关键的作用[1]，因此，对装备系统的可靠性相关指标进行分析与评定就至关重要，而大型复杂系统的可靠性分析与评定又一直是可靠性工程应用中的热点和难点[2]。目前，可靠性分析领域存在3种常用的分析方法：基于可靠性框图和故障树的图形演绎法，基于概率论和马尔可夫链的数学解析法，基于事件和时间的蒙特卡罗仿真分析法[3]。

工程上对系统可靠性进行分析的常用方法还是数学解析法，通过解析法计算公式可以快速地得到系统可靠性结果，但是数学方法因求解困难在应用时存在一定的局限性[2]，目前仅在对指数分布单元的串联系统平均寿命评定问题求解时有简化公式进行计算，对于含有其它常用分布单元（正态分布、对数正态分布和威布尔分布）构成的系统，以及结构复杂系统的平均寿命评定问题的求解因无简化公式则会存在求解困难。

故障树分析方法则是基于图形演绎和布尔运算来分析系统的可靠性问题，在对大型复杂系统可靠性分析时因受NP组合爆炸问题的困扰，同样会导致分析结果很难得到[4]，并且传统的故障树方法是静态的，因此并不能反映出系统故障发生的随机性过程[5]，而动态故障树法在处理复杂系统时同样存在求解困难。

相对于前两种方法，蒙特卡罗仿真方法通过随机抽样、概率模拟和统计分析的方式处理系统可靠性问题，因此能够处理包含不同寿命分布单元与不同可靠性模型的复杂系统的可靠性分析问题，并且能够反映出系统故障的随机性，是大型复杂系统可靠性分析领域中最为普遍的方法[6]。

1 系统任务可靠性的数学计算方法

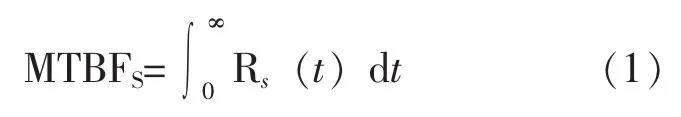
公式（1）是求解平均故障间隔时间的通用公式，适用于任何系统组成结构和寿命分布，但是在对大型复杂系统任务可靠性分析时使用公式（1）求解则会遇到困难，当系统为非串联结构时，系统可靠度Rs（t）较难确定；当系统单元分布为非指数分布时，求积分也将面临巨大的挑战，因此，使用该式对大型复杂系统的任务可靠性分析将很难得到计算结果。

在特殊的情况下，当系统为指数分布单元串联系统时，这时系统中各组成单元的寿命分布服从指数分布，因此各单元的可靠度满足Rt（t）=exp（-λit），其中为常数，从而对于串联系统就有：

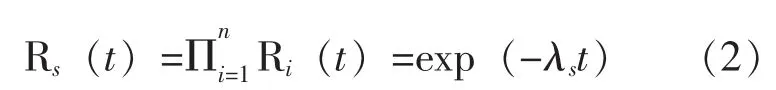
使用数学解析计算方法对系统任务可靠性进行求解时，可以使用公式（1）进行求解[1]。

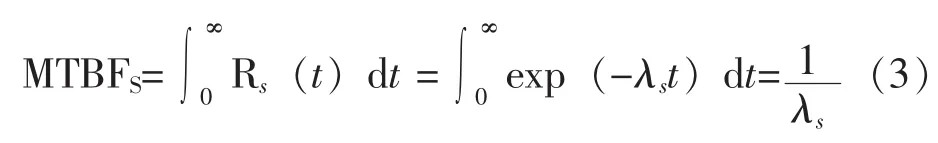
由式（2）和式（3）可得：

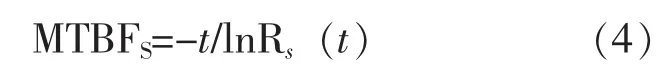
由上可知，公式（4）是系统为指数分布单元串联系统时推导出来的简化公式，该式在工程上常用于对指数分布单元系统基本可靠性的求解，因系统基本可靠性模型就是一个串联模型，这时使用该式方便、准确。但是，实际的复杂系统常含有冗余结构且单元不完全是指数分布，导致使用指数假设推导出的公式（4）存在较大的计算误差，因而在计算复杂系统任务可靠性时该式不再适用。

随着系统复杂度的增加，只能使用公式（1）进行计算，但计算时又会遇到极大的数学困难，因此在实际的工程应用时，使用数学解析计算方法有一定的局限性。

2 蒙特卡罗仿真分析

本文提出采用蒙特卡罗仿真的方法来对系统任务可靠性进行分析计算，通过随机概率抽样的方法来得到近似结果值，从而避免了采用繁杂的数学计算方法以及数学方法应用的局限性。

2.1 蒙特卡罗方法

蒙特卡罗方法（Monte-Carlo方法）亦被称为概率模拟方法，也被称为随机抽样技术或统计试验方法。它是通过随机变量的统计试验、随机模拟来求解工程技术问题的一种近似解方法。其基本思想是：为了求解一个问题，首先建立一个概率模型或随机过程，使它的参数等于问题的解，然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征，最后给出所求问题的解的近似值[5]。蒙特卡罗仿真法的优点是能够反映出系统失效的随机特性，并且使用该方法不受系统复杂性的限制以及能够处理不同概率分布类型的问题[6]。不过也由于其按概率分布随机抽样的随机特性，导致其结果是随机的，只能通过多次试验得到大样本量的试验结果数据，再对结果数据进行统计分析或拟合得到估计值，因此其值也是近似值，当然根据大数定理可知，试验次数越多，估计值也会越逼近准确值，但是，大量的试验次数又会导致程序运行时间的增加。

2.2 系统任务可靠性蒙特卡罗仿真

应用蒙特卡罗方法通常有以下3个步骤：1）构造或描述概率过程；2）实现从已知概率分布抽样；3）建立各种估计量[6]。

应用蒙特卡罗方法求解系统任务可靠性时首先应确定组成系统的各单元的失效时间概率分布，通常对于电子类产品，其失效时间分布服从指数分布，因此在确定概率分布时就是确定其概率分布参数值λ。而对于机械类或机电类产品，其失效时间分布不再服从指数分布，而通常服从其它分布（如正态分布、威布尔分布或对数正态分布），在使用蒙特卡罗仿真方法处理含有机械类或机电类产品的系统时，则需确定符合其分布的相应的分布参数。

确定组成系统的各单元的失效时间概率分布后，再对单元失效时间随机抽样，该值即为在一次试验中该单元的失效时间。

在一次试验中通过随机抽样得到所有单元的失效时间，再由系统可靠性模型得到的逻辑关系来求得该次试验的整个系统的失效时间，系统常用的可靠性模型包括串联、并联、旁联和表决等类型。式（5）-（7）分别给出了串联、并联和旁联模型系统失效时间与其组成单元失效时间的关系，表决模型则可以简化为串并联模型。

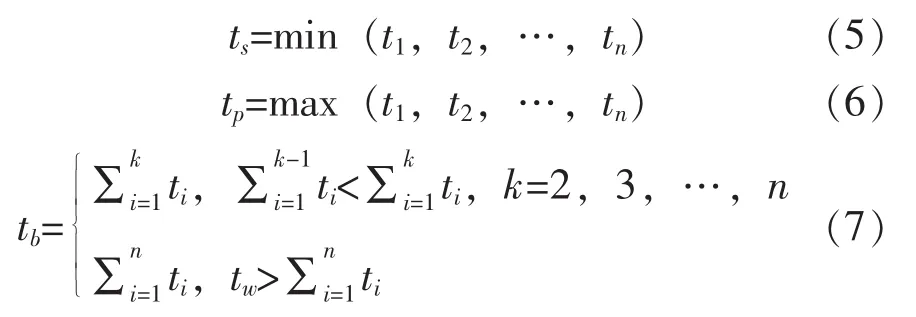
式中，ts，tp，tb分别为串联、并联和旁联系统失效时间；ti（i=1，2，…，n）为组成系统各单元失效时间；tw为旁联系统转换装置失效时间。

由于大型复杂系统的可靠性模型通常由上述几种模型组合而成，因此，式（5）-（7）进行组合就能够表达大型复杂系统与其组成单元失效时间之间的关系，如式（8）所示。

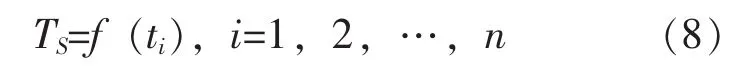
式（8）中：Ts——整个系统的失效时间；

ti（i=1，2，…，n）——组成系统各单元失效时间。

重复N次试验得到N个系统失效时间，通过对N次试验结果进行拟合求均值，得到系统平均致命故障间隔时间（可修系统）或系统寿命时间（不可修系统），最后再计算N次试验中系统失效时间大于规定的任务时间次数与总试验次数的比值，由大数定理可知，该比值在试验次数足够大时可认为是系统失效时间大于规定的任务时间的概率。

由公式（9）可知，该值即是系统任务可靠度值。

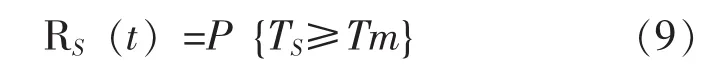
式（9）中：Rs（t）——系统任务可靠度；

Ts——系统的失效时间；

Tm——规定的系统任务时间。

2.3 蒙特卡罗仿真的程序实现

使用MATLAB软件编制了系统任务可靠性蒙特卡罗通用仿真程序，程序流程如图1所示。

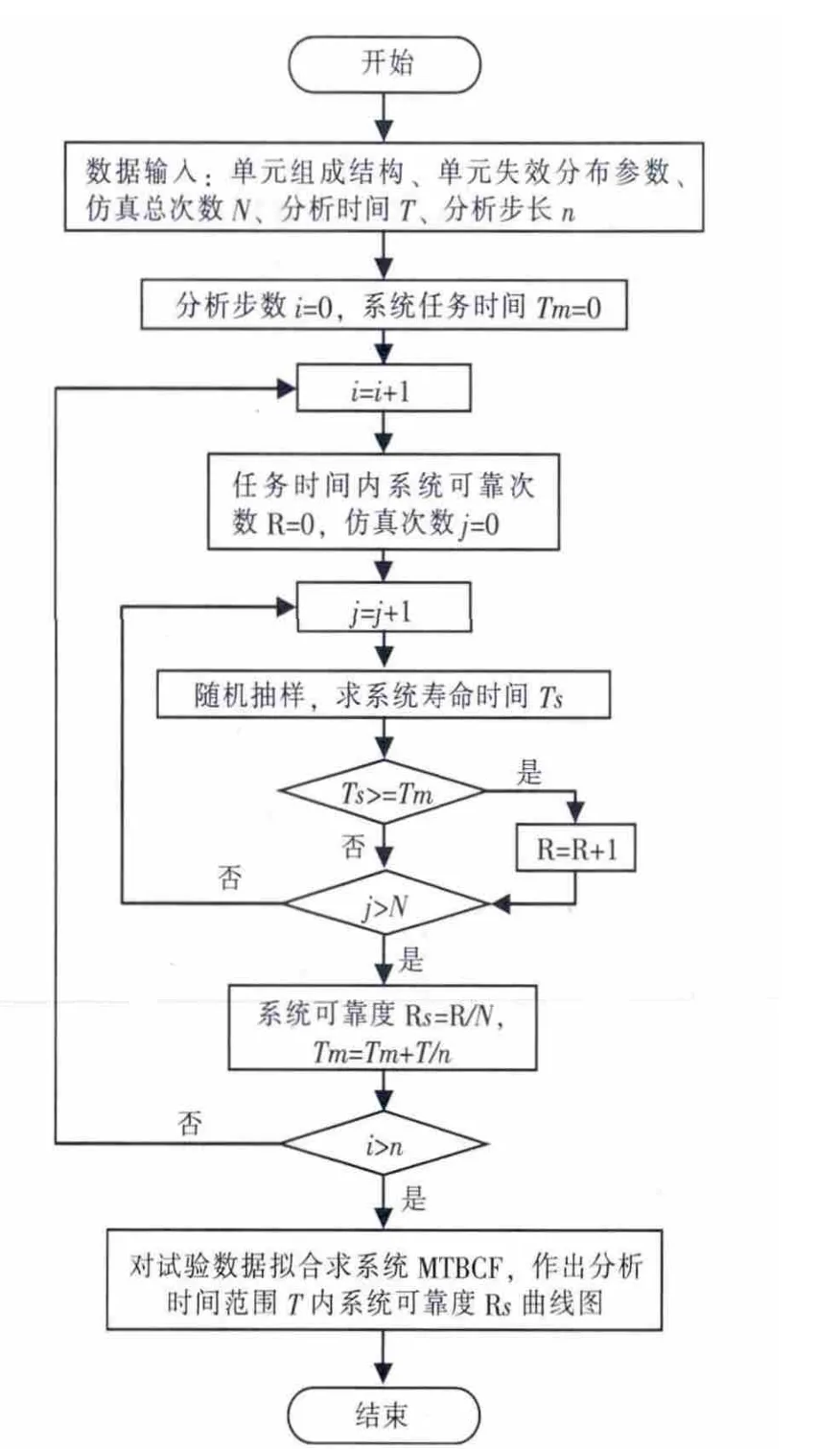
图1 系统任务可靠性蒙特卡罗仿真流程图

运行程序后，通过输入系统模型结构参数、单元失效率和仿真总次数以及分析时间和步长等参数，程序自动执行，最后输出分析结果，包括系统的MTBF值和分析时间内的系统可靠度曲线图。

3 算例分析

3.1 程序验证

分别以指数分布单元的简单串联、并联、旁联和表决模型为例，通过比较解析计算结果和仿真分析结果来验证程序的有效性。解析计算所用的数学模型来源于文献[1]，解析计算结果和仿真分析结果见表1。

表1中所有的仿真结果值都是在仿真次数为5000次时得到的结果，其值与解析计算值的误差在可以接受的范围内，证明了程序的有效性。

3.2 实例分析

3.2.1 实例 1

以文献[4]中车辆上的电动助力器系统可靠性模型为例，对系统进行仿真分析，模型图如图2所示，各单元名称、失效分布及可靠性参数见表2，旁联转换开关完全可靠。

图2 电动助力器系统可靠性框图

仿真次数为5000次时，蒙特卡罗仿真分析得到系统的平均致命故障间隔时间MTBCF为397.2 h，系统在0～1000 h内的可靠度曲线如图3所示。

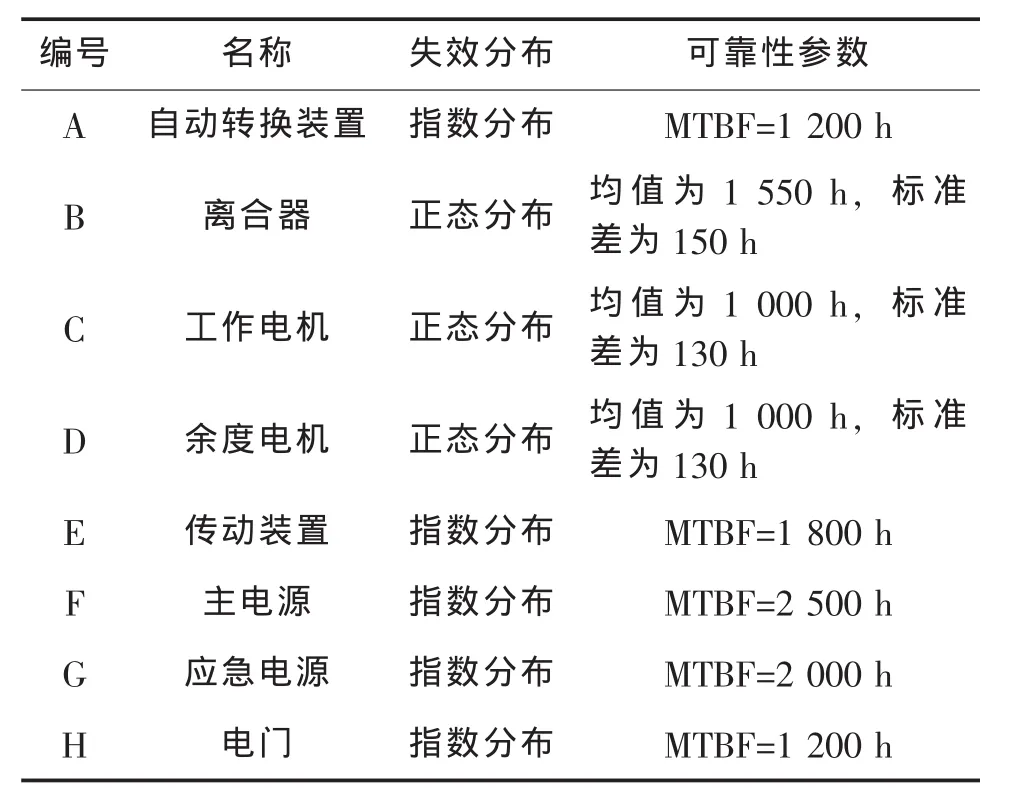
表2 电动助力器系统单元失效分布和参数列表

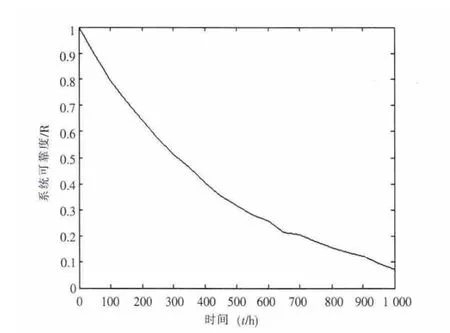
图3 电动助力器系统可靠度曲线

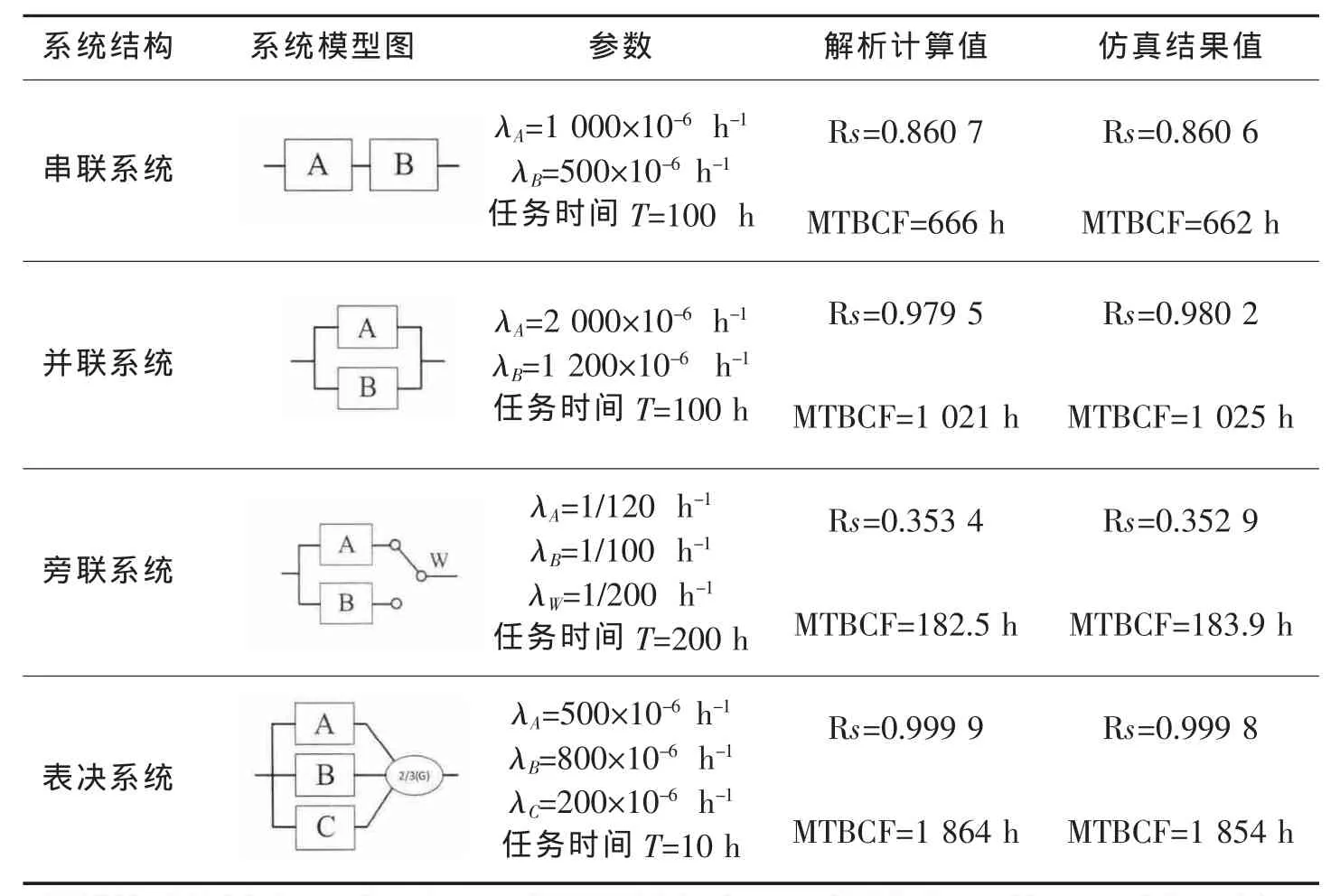
表1 仿真结果和理论结果比较

该实例中组成单元不再仅仅服从指数分布，而是包含了正态和指数分布类型，这时使用数学解析方法进行计算会相当困难；但是，如果利用蒙特卡罗仿真方法则较为简单，最后分析得到电动助力器系统的平均致命故障间隔时间为 397.2 h，该值与文献[4]中得到的分析结果一致，验证了程序的有效性，也证明了蒙特卡罗仿真分析法在大型复杂系统的可靠性分析中的可用性。

3.2.2 实例 2

以文献[8]中给出的某型机载交流电源系统为例，对系统进行仿真分析，模型图如图4所示，各单元名称、失效分布及可靠性参数见表3。

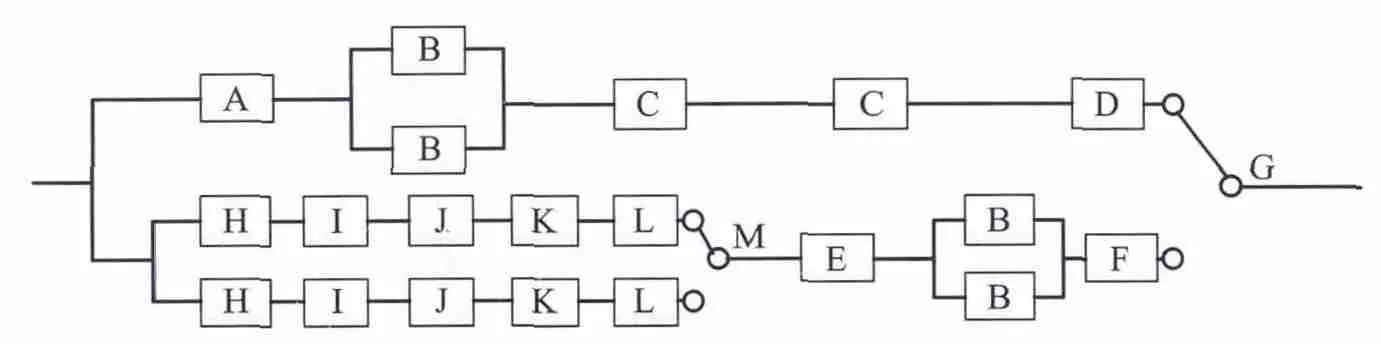
图4 某型机载交流电源系统可靠性框图

表3 某型机载交流电源系统单元失效分布和参数列表

仿真次数为5000次时，蒙特卡罗仿真分析得到系统的平均致命故障间隔时间MTBCF为781.5 h，系统在0～1000 h内的可靠度曲线如图5所示。

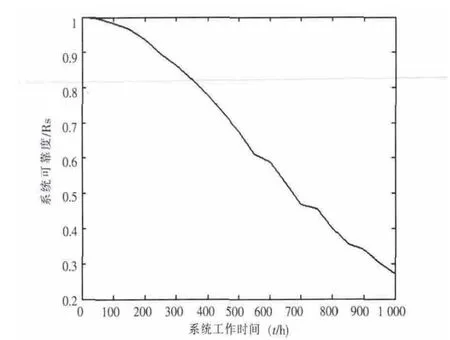
图5 某型机载交流电源系统可靠度曲线

通过该例说明了蒙特卡罗仿真分析法在大型复杂系统的可靠性分析中的应用。

4 结束语

本文使用蒙特卡罗仿真技术对系统的任务可靠性进行分析和评定。通过蒙特卡罗的随机概率分布抽样来模拟系统单元的失效过程，不仅能更好地描述系统失效的随机性过程，同时还能处理单元分布不为指数分布的情况，其应用范围几乎包括各种分布类型各种组成结构的大型复杂系统，相比于工程上主要使用的数学解析方法，应用范围更广。

利用MATLAB软件编制的系统任务可靠性蒙特卡罗通用仿真程序，使用简单，只需按系统结构并根据程序要求输入各结构单元分布参数和仿真信息参数，程序即可自动地进行仿真分析，并显示分析结果。该程序通过了多个算例的验证，证明了程序的有效性。

但是蒙特卡罗方法本身属于一种随机抽样方法，所以其结果值也是一个随机值，虽然这种随机处理方法和实际系统失效的随机性相似，但在最后对数据处理时，会由于结果的随机性导致最终所求估计值的误差，因此在使用中为了减少误差，会采用提高仿真试验次数的方法，但这样同时也会导致程序分析时间的增加，在使用中需要找到这两个矛盾的平衡点。

[1]丁定浩，陆军.装备寿命周期使用保障的理论模型和设计技术[M].北京：电子工业出版社，2011.

[2]金星，洪延姬.大型复杂系统平均寿命评定的Monte Carlo方法[J].系统仿真学报，2005，17（1）：66-68.

[3]张玉涛，唐俊，张明清，等.基于蒙特卡罗方法的可靠性仿真过程模型研究[J].系统工程与电子技术，2008，30（7）： 1374-1377.

[4]喻华，魏来生.改进的故障树Monte-Carlo数字仿真[J].车辆与动力技术，2006（3）：35-37.

[5]杨为民，盛一兴.系统可靠性数学模拟[M].北京：北京航空航天大学出版社，1990.

[6]任文杰，王伟，王丽君，等.蒙特卡罗仿真在飞控系统可靠性评估中的研究[J].计算机仿真，2009，26（4）：63-66.

[7]肖刚，李天柁.系统可靠性分析中的蒙特卡罗方法[M].北京：科学出版社，2003：36-44.

[8]陆中，孙有朝.基于Monte Carlo法与GA算法的复杂系统可靠度求解[J].系统工程与电子技术，2008，30（12）： 2519-2522.