精密单点定位的数学模型选择
2013-08-13鲍建宽陈伟荣高成发
鲍建宽,陈伟荣,高成发
(1.黑龙江工程学院 测绘工程学院,黑龙江 哈尔滨150050;2.东南大学 测绘工程系,江苏 南京210096)
GPS技术为测量定位带来了巨大的进步,目前常用的主要有传统单点定位和差分GPS定位。传统的标准单点定位(Standard Point Positioning,SPP)尽管只需1台GPS接收机就可以进行实时的导航定位,且在导航领域具有广泛的应用,但精度低(数米至数十米),满足不了许多高精度定位用户的精度要求;差分GPS定位(DGPS)技术虽然精度高,但需要布设至少1个基站,作业时,不仅受作业距离的限制,仪器成本和劳动成本都相应增加不少。
Zumbeger于1997年提出精密单点定位技术(Precise Point Positioning,PPP),利用IGS提供的精密星历和精密卫星钟差,对单台GPS接收机所采集的相位和伪距观测值进行定位解算,在一定条件下能够达到与差分GPS技术相当的定位精度,在处理单机静态观测数据时取得了厘米级的定位结果。
GPS精密单点定位技术单机作业,机动灵活,作业不受作用距离的限制。它集成了标准单点定位和差分定位的优点,克服了各自的缺点,具有广阔的应用前景。作为一项GPS定位新技术,精密单点定位技术在高精度静态定位、精密时间确定和时间传递以及对流层参数估计等方面都有成功的应用。目前,主要有3种定位模型,即传统消电离层组合模型、UofC模型和无模糊度模型。
1 GPS精密单点定位常用模型
1.1 传统模型
传统模型采用码和相位的消电离层组合作为观测量,每颗卫星对应2个观测量,Zumberge、Kouba和Heroux等人均使用该组合值作为精密单点定位的函数模型。双频观测值P1,P2线性组合,得到消除电离层影响的伪距组合观测值和相位组合观测值,具体形式如下:
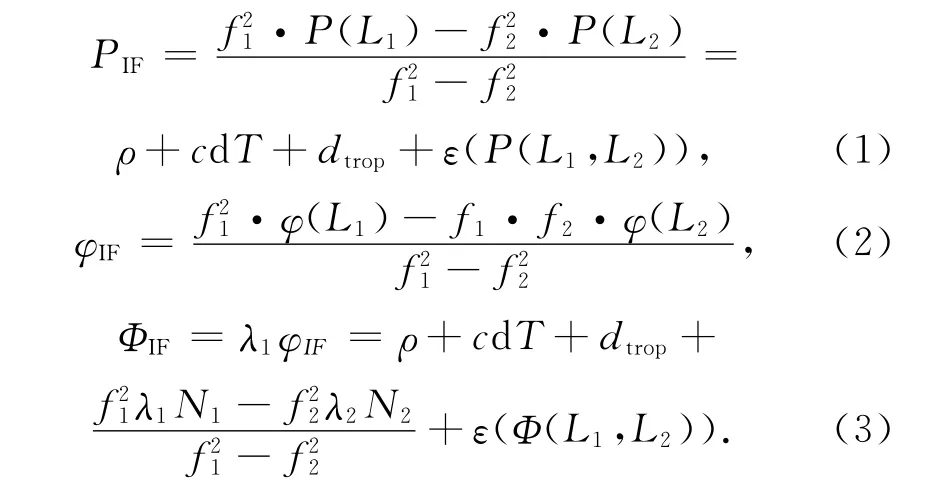
式中:P(Li)为Li上的伪距观测值,Φ(Li)为Li上的载波相位观测值,PIF为无电离层延迟的伪距组合值,ΦIF为无电离层延迟的载波相位组合值,ρ为站星几何距离,c为光速,dT为接收机钟差,dtrop为对流层延迟,λi为Li波长 ,ε(.)为包括多路径影响等观测噪声。
1.2 UofC模型
UofC模型采用伪距和相位的半和组合以及相位的消电离层组合作为观测量,每颗卫星对应3个观测量,由Calgary大学的Gao Yang于2002年提出[3]。具体形式如下:
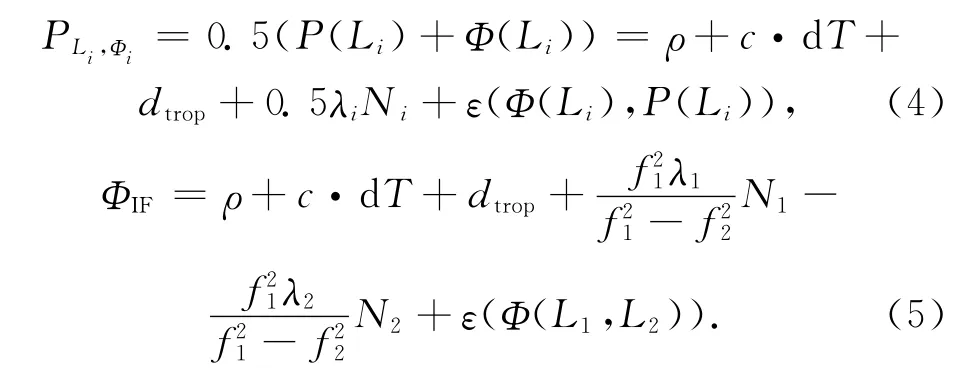
式中:PLi,Φi为伪距和载波相位观测值平均值,半和组合。
在UofC模型中,2个载波上的模糊度是分别估计的,采用模糊度伪固定(Pseudo-Fixing)的方法加速模糊度收敛,由于观测量作了半和组合,观测噪声只有伪距噪声的0.5倍。
1.3 无模糊度模型
传统模型与UofC模型都是非差模型,每颗卫星都可以对应列出2个或3个方程;而无模糊度模型是差分模型,它在传统模型的基础上,对相邻历元间的载波相位观测值差分,从而消除模糊度项,不必再考虑模糊度的估计。模型具体形式为
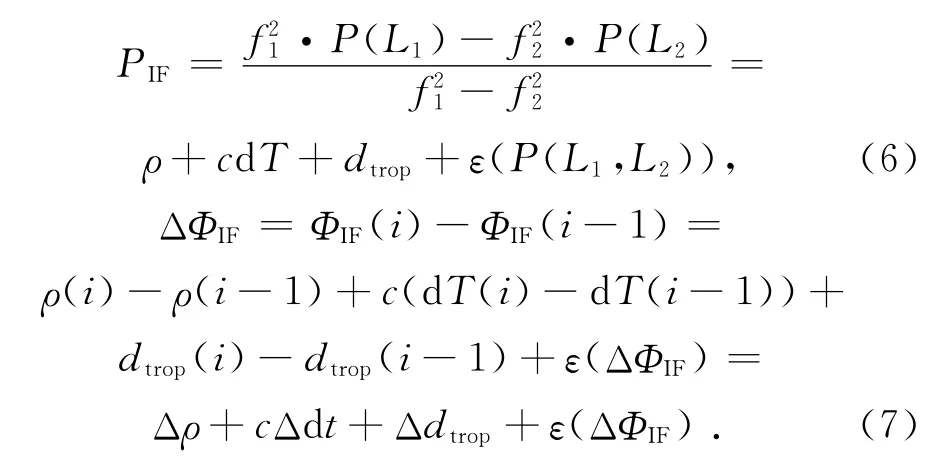
式中:ΔΦIF为历元i与i-1时刻无电离层相位组合观测值之差,Δρ为站星几何距离之差,Δdt为接收机钟差之差,Δdtrop为对流层延迟之差。
1.4 3种常用模型的比较
3种常用模型的比较见表1。

表1 3种常用模型的优缺点分析
2 差分观测值的GPS精密单点定位
传统模型和UofC模型都是非差观测值的模型,是目前最常用的精密单点定位模型。借鉴GPS相对定位中,采用单差、双差和三差观测值来消除和减弱各种误差影响,在精密单点定位中也可以采用差分观测值的方法。
2.1 星间差分
同一历元不同卫星之间求差,组成单差模型的精密单点定位观测方程。某历元时刻,卫星l的载波观测方程

同一时刻,卫星k的载波观测方程
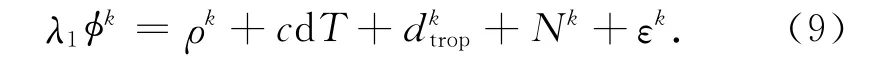
式(8)和式(9)两式相减,得到星间差分观测方程
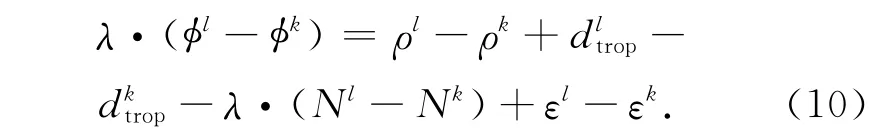
由方程(10)可以看出,接收机钟差项被消除。
2.2 历元间差分
即常用定位模型中的无模糊度模型,相邻历元间求差,组成单差观测方程。具体方程见式(7),历元间做差后消除了模糊度参数项。
2.3 星间历元间二次差分
在星间差分的基础上,相邻历元间再做差,组成二次差观测方程。历元i时刻星间单差方程
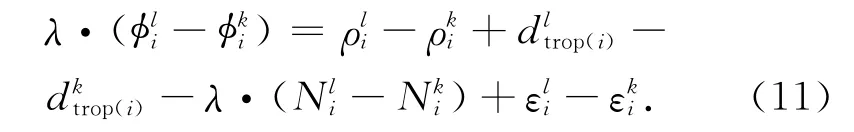
相邻下一历元j时刻星间单差方程

二次差分是最简单的观测模型,模糊度参数和接收机钟差都被消除了。
2.4 不同差分模型的比较
不同差分模型的比较见表2。

表2 差分模型的优缺点分析
差分模型相比于非差模型的优势是很明显的,减少未知数的个数,简化计算,减少参数的估计收敛时间。但同样地,差分模型的缺陷也很突出,观测值的相关性是一大难题。
3 组合新模型
通过上述对现有模型各自优缺点的分析,在此基础上引入星间历元间二次差,即对传统模型同一历元不同卫星求差,然后相邻历元间再做差;因二次差模型大大增加观测量的相关性,所以二次差模型求解的测站坐标与权阵仅作为卡尔曼滤波器的初始值,然后以星间一次差为模型求解测站坐标和模糊度等参数,即二次差 — 一次差组合新模型。
3.1 模型推导
假设在历元i与历元j都能观测到n颗卫星,下面分析和推导组合新模型。
步骤一:历元i观测卫星l的消电离层组合观测值的观测方程
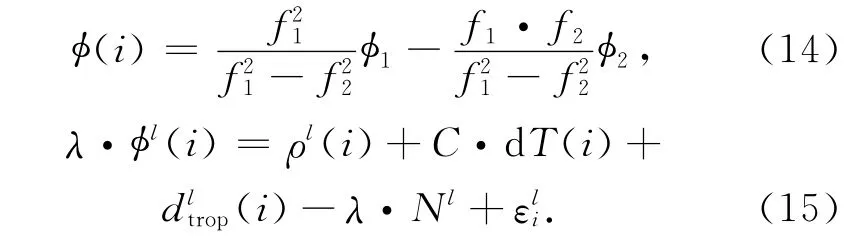
步骤二:选取历元i中高度角最大的卫星k作为参考卫星,则参考卫星的消电离层组合观测方程为

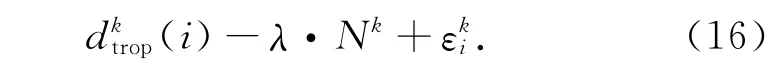
步骤三:式(14)与式(15)两式相减,得到历元i时刻卫星之间求差后的观测方程

步骤四:两个历元i与j之间再做差,组成星间历元间二次差的观测方程
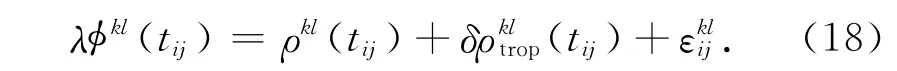
步骤五:以方程(18)为模型,线性化后用卡尔曼滤波方法求解,解算结果作为滤波初始值,再以方程(17)为模型,线性化后求解。
利用二次差—一次差组合新模型进行GPS精密单点定位,克服了星间历元间二次差模型的缺点,即观测值的相关性。二次差的结果仅仅作为滤波初始值,以较精确的初始值来加快卡尔曼滤波的收敛时间,达到快速收敛的效果。而星间一次差则消除了接收机钟差的影响,减少了未知数个数,解决方程病态和奇异问题,利用少量历元就可以估计参数,大大提高了观测资料的利用率。
3.2 精度分析
二次差— 一次差组合新模型的实质还是星间差分模型,二次差仅用作计算滤波初值。采用星间差分,就会存在观测值相关性问题。
传统消电离层组合观测值ΦIF观测噪声是原始伪距和载波相位观测噪声的3倍,卫星间差分模型是在传统模型基础上,同一历元不同卫星之间求差,观测噪声是传统模型的倍,也就是原始观测噪声的4倍多,可以满足厘米级定位精度的需要。
4 定位试验及结果分析
4.1 试验资料综述
为了分析差分模型与传统非差模型在精密单点定位的精度、收敛时间方面差异,本文取2007年4月,用Leica530GPS在南京已知基准点上采集的静态观测数据,历元间隔为5s,观测时卫星数目为6~8颗,卫星截止高度角为10°。从IGS网站下载同一时段的精密星历与精密钟差文件,用自己编写的精密单点定位软件,使用不同的模型分别进行单点定位的解算,并对解算结果进行对比分析。
由于GPS观测的历元间隔为5s,需事先对精密星历与钟差文件进行拉格朗日差值,观测数据文件也需要预处理,剔除粗差和修复周跳。另外,各项能够模型化的误差也已通过计算得到。
4.2 试验结果
图1是采用传统非差模型进行精密单点定位的空间坐标收敛情况。由图1可以看出,1 000s以后,空间坐标趋于收敛,而具体数据表明,2 500s以后,该点位在XYZ3个方向上的定位精度达到厘米级。
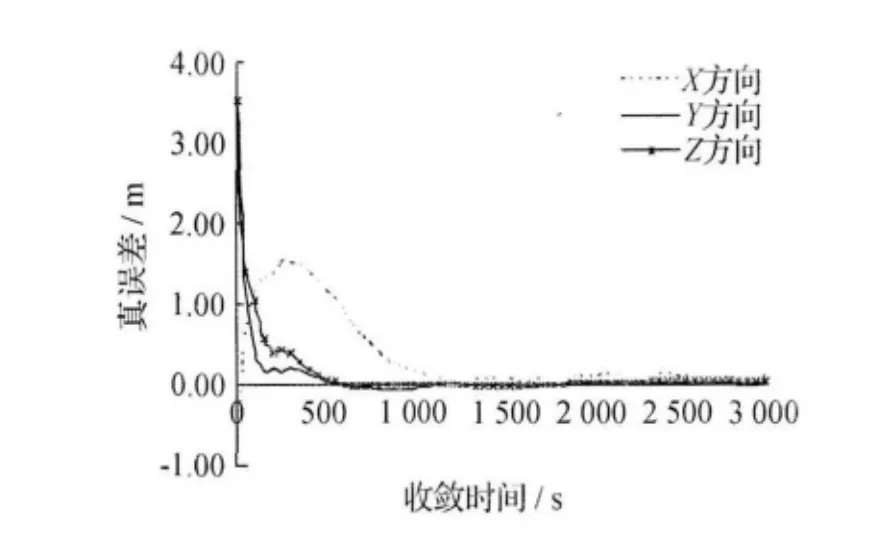
图1 传统模型(非差)精密单点定位在空间坐标XYZ的残差
图2 是采用星间单差模型进行精密单点定位解算的坐标收敛统计图。由于消除了接收机钟差的影响,未知参数只剩下点位坐标,模糊度和对流层延迟。与非差模型相比,稳定性不足,在600s附近X方向残差有变大趋势,到2 000s附近收敛到厘米级精度,收敛时间相比非差模型要快一些。
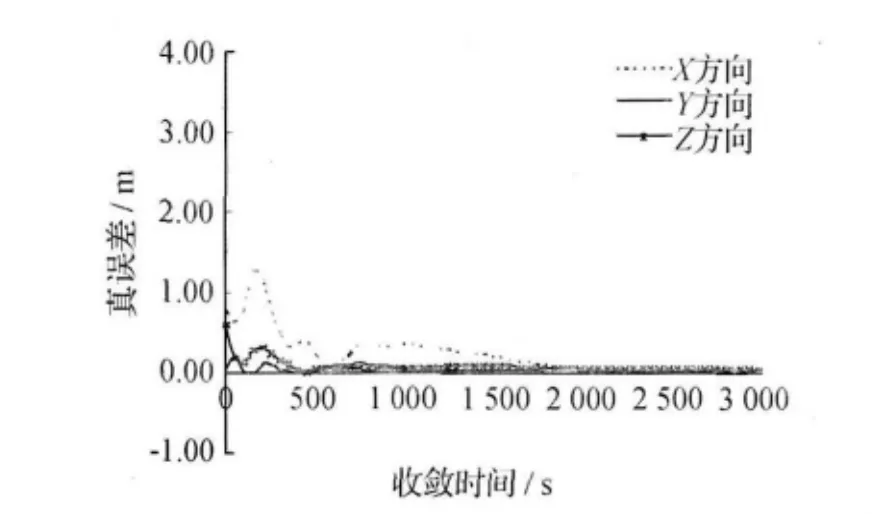
图2 星间单差模型精密单点定位在空间坐标XYZ的残差
图3 是采用星间历元间二次差模型,相比于非差和单差模型,二次差模型的参数项更少,无模糊度项,无接收机钟差项,是最简单的观测模型。结果显示:X 方向残差在1 000s附近有反弹,且3 000s的时候还没有收敛到厘米级,YZ方向收敛比较稳定快速。这主要是因为二次差观测值之间的相关性大大增强,不利于解算。
图4采用组合新模型的精密单点定位结果统计,因同样是采用的差分模型,收敛在1 000s附近有反弹,不到2 000s的时候达到厘米级精度。
表3是几种试验模型收敛到厘米级精度的时间统计。根据表3数据,传统非差模型收敛时间长,星间单差模型收敛时间较短,而二次差模型在3 000s的时候还没有收敛到厘米级精度,组合新模型比星间单差收敛时间更快,近30min的时间就能达到厘米级精度要求。
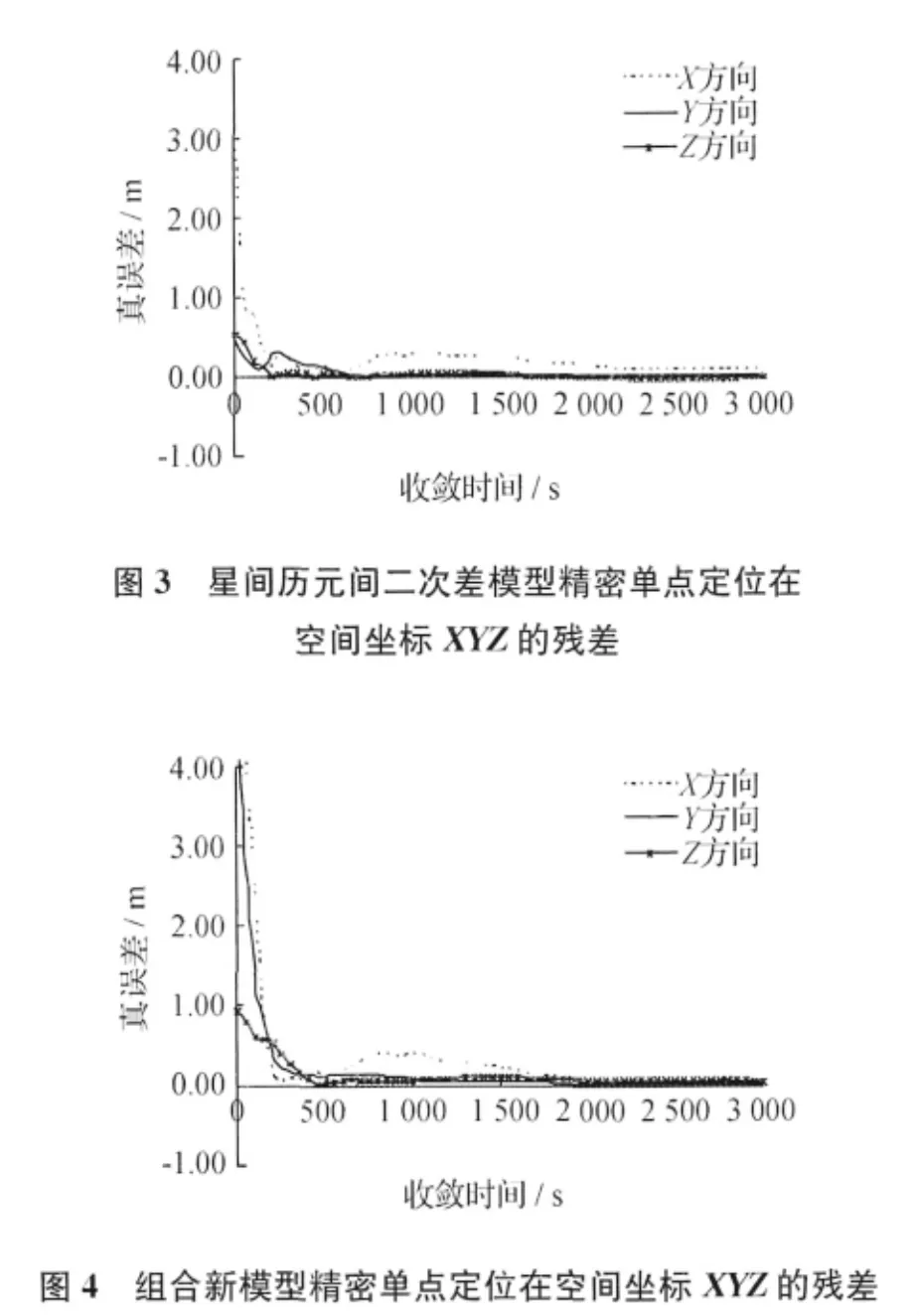

表3 4种试验模型收敛到厘米级精度的时间统计
比较结果可以看出,由于各种模型的组合观测值的构造方式不同,在定位结果收敛速度上稍有差异,传统模型稳定,而组合新模型定位快。虽然定位过程中,组合新模型的收敛有反弹过程,总体影响不大,是一种比较好的单点定位模型。
5 结束语
精密单点技术是目前GPS研究领域的热点方向之一,具有很强的技术优势。特别是在一些不适合建立CORS基站的地形复杂或地域庞大的地区,精密单点定位技术不依赖于基站,大大提高作业效率。然而,精密单点定位目前仍然存在不少问题,包括定位模型、误差改正、数据预处理、参数估计等。本文对精密单点定位的定位模型方面做了一些尝试,在分析比较几种非差和差分模型之后,提出二次差 — 一次差组合新模型。通过精度分析,组合新模型能够满足厘米级单点定位的要求。试验结果也表明,采用组合新模型能改善单点定位的作业效率,更快速地达到精度要求。
[1]Zumberge J F.,Heflin M B.,Jefferson D C.,et al.Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J].Journal of Geophysical Research,1997,102(B3):5005-5017.
[2]Liu Jingnan,Ye Shirong.GPS Precise Point Positioning Using Undifferenced Phase Observation[J].Geomatics and Information Science of Wuhan University,2002,27(3):234-240.
[3]Gao Yang,Shen Xiaobing.Improving ambiguity convergence in carrier-based precise point positioning[C].ION GPS 2001,Salt Lake City,USA,2001:1532-1539.
[4]郑作亚,卢秀山.基于加权的伪距和历元间相位差分模型GPS单点定位方法[J].测绘科学,2007(5).
[5]李浩军,王解先,胡丛玮,等.基于历元间差分技术的精密单点定位研究[J].宇航学报,2010(3).
[6]祁芳.卡尔曼滤波算法在GPS非差相位精密单点定位中的应用研究[D].武汉,武汉大学,2003.
[7]曹相,高成发.GPS精密单点定位(静态)影响收敛速度的因素分析[J].现代测绘,2007,30(1):19-21.
[8]郝明,丁希杰.GPS精密单点定位的数据处理方法综述[J].测绘工程,2008,17(5):60-62.
[9]吴江飞,黄珹.GPS精密单点定位模型及其应用分析[J].大地测量与地球动力学,2008(2):96-100.
[10]林瑜滢,阮仁桂,黄健,等.动态精密单点定位传统模型与UofC模型的比较[J].测绘科学技术学报,2010(2):31-34.
