考虑弯曲刚度的悬索自由振动解析解
2013-08-13卓卫东范立础
肖 一,卓卫东,范立础
(1.福州大学 土木工程学院,福建 福州 350108;2.同济大学 桥梁工程系,上海 200092)
悬索的自由振动是一个古老的问题,而自1940年Tacoma桥风毁后,其又吸引了众多学者的关注。Pugsley,Saxon,Goodey等人[1]对悬链的自由振动进行了深入研究 ,Simpson[2],Irvine[3],Triantafyllou[4]等人则推导了弹性索的自由振动解析解,尤其是Irvine的工作对其后的研究影响深远。但是,这些研究均未考虑弯曲刚度的影响。为更准确地计算悬索的自振频率,有时应计入弯曲刚度的影响,尤其对于截面较大的拉索[5-6],而关于振动法测索力的研究[7-9]一般均考虑了弯曲刚度的影响。文献[10-11]则用半解析方法对考虑弯曲刚度的斜索固有振动问题进行了研究。
最近,文献[6]在抛物线假设下推导了考虑弯曲刚度的悬索面内自由振动解析解,但其仅考虑了两端固接边界条件;文献[12]在其已有研究基础上计入弯曲刚度影响推导了斜索面内固有振动解析解,但其仅考虑了两端铰接边界条件。从文献[13]的图中可知,锚固端的约束条件可能为固接(直接锚固连接),也可能为铰接(如锚头和锚板采用铰接形式),如文献[5,14]就对两种情况进行了分析,而实际的情况往往是处于两种状态之间[8]。
当不考虑弯曲刚度对静力构形的影响时,悬链线是较抛物线更接近实际情况的表达。本文以悬链线为索静力构形,分别考虑两端固结和两端铰接两种边界条件对考虑弯曲刚度影响的悬索自由振动解析解进行了推导,对已有的结果进行了补充并纠正了文献[6,12]中的不当之处,最后对结果进行了讨论。
1 理论推导
如图1所示的做微幅运动的空间悬索,其坐标原点置于左端点。

图1 悬索计算图示
当考虑弯曲刚度时,在不计阻尼和动力荷载情况下,悬索的面内和面外线性运动方程分别为[6]:

其中:w和v分别为索z和y方向运动分量;H为索静拉力水平分量;h为H的动力增量;EI为截面抗弯刚度;m为单位长度质量。这里假设索截面在面内和面外有相同的抗弯刚度。由式(1)和式(2)可知,面内和面外运动不耦合。


由于索以承受轴向力为主,这里仅考虑由轴力产生的应变而忽略弯曲应变,此时有线性化的索方程[3]:

其中:u为x方向运动分量;s表示弧长。对其进行无量纲化并考虑到两端为固定的边界条件可得:

其中,λ2=(mgl/H)2l/(HLe/EA)为 Irvine[3]引入的参数,其反映了索弹性效应和几何效应的影响;Le为索有效长度[3];EA为索轴向刚度。
1.1 面外振动
文献[6,12]中并未给出面外振动解,这里首先对其做一个补充,以便于后文的讨论。
易知式(4)的通解为:

其中:

两端固接时有:

两端铰接时有:

可见,其解与受拉梁的结果[15-16]一致。这也体现了线性振动时,垂度效应对面外运动是无影响的。
1.2 面内振动
由于结构和边界条件是对称的,分别按反对称和对称两种情况讨论。当振型为反对称形式时=0[3,6,12],此时式(3)的通解为:

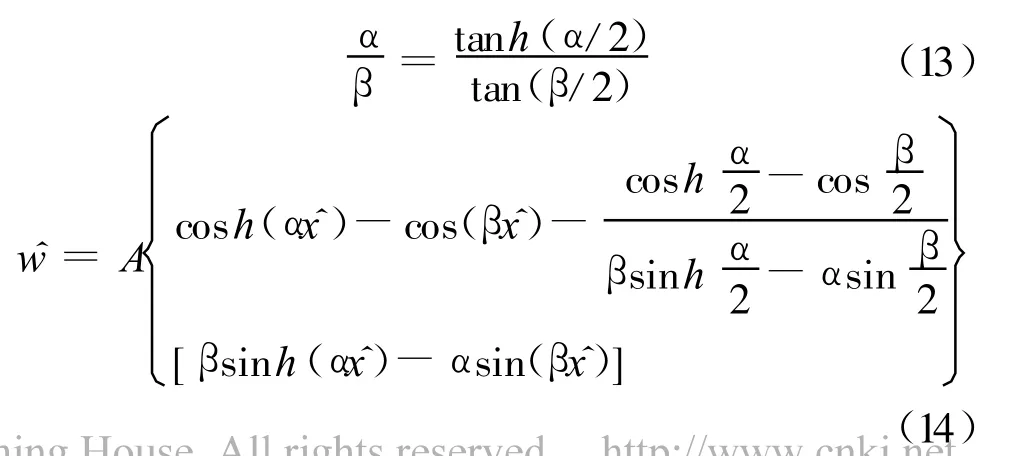
文献[6]也给出了两端固接索面内反对称振动解析解,通过对比发现,其频率方程与本文相同,但振型函数并不满足两端的边界条件。经验证,本文结果是正确的。

这与文献[12]中的结果是不同的,由于采用了不合适的边界条件,其频率和振型中实际上包含对称和反对称部分,而式(15)和式(16)则仅为反对称部分。
这里顺便指出,由于实际上没有考虑垂度的影响,这里求出的反对称解实际上就是受拉梁在相应边界条件下的反对称振动部分,当把上面的中点处的边界条件换为(1/2)=(1/2)=0时,就可得到受拉梁固有振动解的对称部分。当两端固接时有:

两端铰接时则有:

把相应的对称和反对称频率方程相乘即可得到受拉梁固有振动的完整解,由于这里假设面内和面外弯曲刚度相同,其就是式(8)和式(10),这也进一步体现了上面结果的正确性。
当振型为对称形式时,如图1所示,为求解方便,首先将坐标原点移至弦的中点,并沿用原来的符号表示。与文献[6,12]采用的抛物线不同的是,这里采用更为准确的悬链线索形。此时,悬链线表达[17]经坐标变换和无量纲化后得:

其中,k=mgl/H。由此可得式(3)的一个特解为:

则其通解可表示为:


而C2=C4=0,将其带入通解中即可得到振型函数。然后,将所得振型函数带入索方程中(此时由于坐标系的移动,需要修改积分限)并消去≠0后,可得频率方程为:


而C2=C4=0,将其带入通解中即可得到振型函数,而相应的频率方程为:

值得指出的是,式(24)和式(26)只是一种表达形式 ,利用关系式 ξ2=α2-β2,ξˆω=α β 和k4-ξ2k2-ξ2=(k2-α2)(k2+β2),其还可以有其它等效的表达形式。
2 讨 论
文献[6]和文献[12]分别对两种边界条件下的结果进行了数值验证,在λ2的实际取值范围内都有良好的精度。其中,文献[12]的数值方法采用的索静力构形与本文相同。但实际上,由于他们得到的是解析解,这种验证不但是对解的验证,更是对近似运动方程的验证,所以这里就不再对此进行重复。
2.1 边界条件的影响
图2表示参数 ξ分别取20、50、75和200[5-6]四种情况时,两种边界条件下前六阶无量纲频率(ˆω/π)随参数 λ2的变化情况。CC表示两端固接,HH表示两端铰接,Irvine表示文献[3]的解。从图中可见,考虑弯曲刚度的悬索同样会发生Crossover现象[6,10];显然,考虑弯曲刚度的频率要高于不考虑弯曲刚度的情况,两端固结情况则要高于两端铰接情况;频率阶数越高,三者之间的差别越大;参数 ξ越小,也就是弯曲刚度的比重越大时,两种边界条件下的频率差别越大。
由此可见,对于需要考虑弯曲刚度的悬索的动力分析,考虑不同形式的边界条件是必要的。
另外,正如文献[8]指出的,拉索的实际约束情况往往处于固接和铰接之间。本文的两端固结和两端铰接情况相当于实际约束情况的上下界,当需要考虑更精确的约束条件时,由此可以对实际的拉索频率进行近似估计。
2.2 悬链线解与抛物线解对比
文献[6,12]采用的静力解实际上与Irvine[3]相同,其并未考虑弯曲刚度的影响。在忽略该影响的假定下,由于本文采用的是更准确的悬链线索,所以从理论上讲,其精度要高于文献[6,12]的结果。
令文献[12]中的参数ε=0时,就可得到相应的水平索的频率方程。这样,在本文的无量纲表示下,考虑弯曲刚度的抛物线索的两端固接和两端铰接面内对称频率方程分别为[6,12]:

相比于其原始表示,式(27)、式(28)略为简洁。

图2 两种边界条件下参数ξ取不同值时前六阶频率对比

图3 两种边界条件下参数k取不同值时前四阶对称频率对比
图3给出了 ξ=75时 ,k取 0.1、0.5、0.85和1.0时与抛物线解的前四阶对称无量纲频率(ˆω/π)随参数λ2的变化情况。由图3可见,两种构形表达的结果相差很小,仅上升段略有差别,其基本可以忽略(所以图中未标出各曲线的意义),对于ξ取其它值的情况,也可得出类似的结果,这从另一个角度也验证了式(27)和式(28)的正确。所以,相比而言,在实际应用中可以采用式(27)和式(28)。
3 结 语
本文在已有研究基础上考虑了更准确的悬索静力构形——悬链线,推导了在两端固接和两端铰接边界条件下考虑弯曲刚度的悬索面外和面内自由振动解析解,对已有文献结论进行了补充并修正了其不当之处。通过讨论认为,当分析中需要计入悬索的弯曲刚度时,应该要考虑不同边界条件的影响,而本文结果可以看作是实际情况的上下界。通过与已有结果对比发现,本文结果虽从理论上更精确,但其与已有结果的差别在实际应用中基本可以忽略,从这个角度来讲,本文结果也可以看作是对已有理论的一个补充。
[1]Rega G.Nonlinear dynamics of suspended cables,Part I.Modeling and analysis[J].Appl.Mech.Rev.,ASME,2004,(57):443-514.
[2]Simpson A.Determination of the inplane natural frequencies of multispan transmission lines by a transfer matrix method[C]//Proceedings of the IEEE,1966,113(5):870-878.
[3]Irvine H M,Caughey T K.The linear theory of free vibrations of a suspended cable[C]//Proceedings of the Royal Society of London Series A,1974,341:299-315.
[4]Triantafyllou M S.The dynamics of taut inclined cables[J].Quarterly Journal of Mechanics and Applied Mathematics,1984,37(3):421-440.
[5]Ni Y Q,Ko J M,Zheng G.Dynamic analysis of large-diameter sagged cables taking into account flexural rigidity[J].Journal of Sound and Vibration,2002 ,257(2):301-319.
[6]Ricciardi G,Saitta F.A continuous vibration analysis model for cables with sag and bending stiffness[J].Engineering Structures,2008,30(5):1459-1472.
[7]Zui H,Shinke T,Namita YH.Practical formulasfor estimation of cable tension by vibration method[J].Journal of Structural Engineering,ASCE,1996,122(6):651-656.
[8]Kim G H,ParkT.Estimation of cable tensionforce using the frequency-based system identification method[J].Journal of Sound and Vibration,2007,304(3-5):660-676.
[9]任伟新,陈 刚.由基频计算拉索拉力的实用公式[J].土木工程学报,2005,38(11):26-31.
[10]赵跃宇,周海兵,金 波,等.弯曲刚度对斜拉索非线性固有频率的影响[J].工程力学,2008,25(1):196-202.
[11]吴 晓,黎大志,罗佑新.斜拉索非线性固有振动特性分析[J].振动与冲击,2003 ,22(3):37-39,11.
[12]吴庆雄,李 浏,陈宝春.考虑弯曲刚度的拉索面内固有振动的理论计算公式[J].工程力学,2010,27(11):9-15,27.
[13]严国敏.现代斜拉桥[M].成都:西南交通大学出版社,1996:60-68.
[14]Mehrabi A B,Tabatabai H.Unified finite difference formulation for free vibration of cables[J].Journal of Structural Engineering,ASCE,1998,124(11):1313-1322.
[15]Bokaian A.Natural frequenciesof beams under tensile axial loads[J].Journal of Sound and Vibration,1990,126:481-498.
[16]Humar J L.Dynamicsof Structures[M].AA Balkema Publishers,2002:829-876.
[17]Pugsley A.The theory of suspension bridges[M].Edward Arnold,Paris,1957:21-25.
