块体滑落模型实验与三维数值分析
2013-12-20饶文杰金冬梅
饶文杰,汪 江,金冬梅
(东北大学 资源与土木工程学院,辽宁沈阳110819)
随着岩体隧道、边坡等工程的大量新建,工程岩体稳定性和安全性问题成为理论研究和现场施工中重点关注的焦点和难点,尤其碎裂岩体是工程中常见的不良岩体[1],既是非连续体也是非均匀体,在扰动的过程中都极易发生岩体结构损伤,诱发工程灾害。因此,对于岩体开挖诱发的关键块体识别十分重要,现场开挖方案选择和支护措施充分考虑关键块体的规模、大小和方位,这些关键块体[2-5]的形成除了与工程岩体结构面的存在方位密切相关,也与工程因素密不可分。
岩体是一种典型的非连续介质,发育于岩体中各种不同成因的断层、节理、破碎带等结构面相互切割,形成了具有非连续特征的岩体结构,这种结构决定了岩体的宏观变形、强度特征[6]。边坡工程主要设计施工对象即为工程岩体,其开挖及支护方案和参数的选取跟其开挖临空面的岩体与其结构和力学性质密切相关[7],而工程岩体主要与结构面的发育程度、发育位置、产状、组合特征及其工程性质有着十分密切的内在联系[8],如何反映工程岩体的结构面分布以及岩体开挖后的变形破坏,对于边坡工程的开挖及支护十分重要。
本文在211实验室变角度空间块体滑落模型平台实验的基础上,利用基于离散元法开发的3DEC程序对岩质边坡进行三维模拟,建立关键块体的非连续变形动态分析模型,得到动态位移图,对边坡工程的开挖支护有一定借鉴意义。
1 变角度空间块体滑落模型实验
1.1 实验平台
工程中的碎裂岩块在空间受力复杂,所处的自然环境变幻莫测,对岩块滑落分析有限,而模型平台可以模拟工程中不同部位块体滑落过程。它的创新之处在于可改变空间角度,两次变角,进行微小的调动,可观察楔块是否滑落,也可利用不同的模具来模拟工程中不同的岩体情况,进而对岩体的稳定性进行相关研究。
变角度空间块体滑落模型试验平台由主体空间变角度装置和试块以及与试块接触模拟的结构面组成,如图1。主体装置主要是底板和倾斜台两块钢板组成,倾斜台上设有直径为500 mm的圆形加工钢板旋转台,上附0°~360°的圆形刻度盘,模拟的结构面和块体可以通过旋转台上的固定装置进行调整,结构面的产状可以由底板和倾斜台之间的标尺定量的读出。通过改变平台的转向转角,实现了结构面倾向、倾角任意变换的功能。可以模拟不同产状的结构面,并且可以分析在这个过程中块体的稳定性和滑落过程。
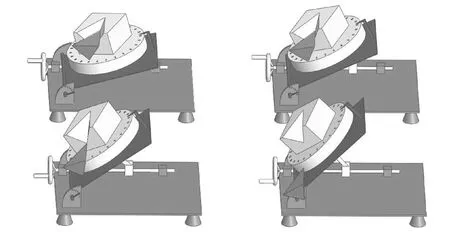
图1 变角度空间块体滑落实验平台
1.2 块体试样及材料选择
岩质边坡失稳模式有平面、圆弧、楔体、倾倒、溃决等多种失稳模式,工程中常见的是平面滑动、圆弧滑动、楔体破坏和倾倒破坏。而楔体破坏是岩质边坡的一个主要的失稳模式,其滑动有两种模式,即单面滑动和双面滑动[9]。楔形块体组成的基本边界条件主要是各种结构面与边坡坡面,由两种结构面组成的楔形体,四面体是最基本的几何体。
本试验以四面体为研究对象进行分析,不计入动力学影响,通过改变块体结构面的倾向和倾角模拟块体的滑落过程,进而研究结构面上块体的稳定性。考虑实验条件及工程岩体的特性,试验中采用的楔形块体与结构面为精磨的大理岩材料以及自制的模具和浇筑的水泥砂浆试件,如图2。

图2 实验试样
1.3 试验过程及结果分析
选择一种横断面角为60°的一组试块和结构面,试样分别采用大理岩和水泥试样,将楔形块体与模拟的结构面固定到变角度空间块体滑落模型试验平台,调试装置的地脚使整个模型处于水平状态。通过控制变量的方法进行试验,按照10°为单位旋转钢板旋转台,再转动手轮,使倾斜台在竖直方向进行角度改变,直至楔形块体滑落,选择4组同样的试块,通过底板与倾斜台之间的角度标尺,分别记录滑落时的空间角度,取其平均值,结果见表1,其中 α表示旋转角,β表示倾斜角。
按照上述方法,选取断面角为60°的砂浆模具和同种材料的水泥砂浆试样,分别做4组实验,记录块体滑落的旋转角、倾斜角,取其平均值,结果见表2。

表1 大理岩块体的滑落角度

表2 水泥砂浆块体的滑落角度
两种材料试块滑落时的旋转角、倾斜角如图3,从图3中可以看到试验模型旋转角处于0°~40°时,试块滑落时的倾斜角度增幅不大;当旋转角度处于50°~80°时,滑落时的倾斜角与旋转角近似呈线性增长,因此可以初步断定当旋转角处于40°~50°之间的某个角度时,为楔形块体双面滑落与单面滑落的分界角度,当旋转角度处于 90°~180°之间时,块体沿一侧的结构面滚落,在数据结果中并未处理。实验结果表明浇筑的水泥砂浆试样总体滑落的倾斜角度要大于大理石材料试样滑落的倾斜角度,一是因为两组材料各自之间的摩擦系数不同,二是浇筑的水泥砂浆试样中由于养护的原因出现不平滑的表面,在滑落的过程中会与接触的模具有一定的咬合力,从而阻止了块体的滑落。
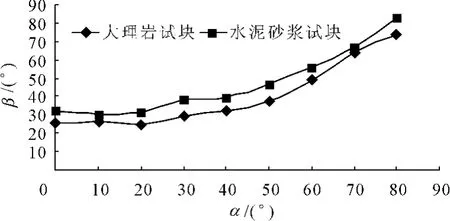
图3 大理岩和水泥砂浆块体的滑落角度比较
2 块体滑落实验数值分析
2.1 数值分析思路和方法
结合变角度空间块体滑落模型实验的实验结果,应用基于离散单元法作为基本理论的程序3DEC对其滑落过程及结果进行模拟分析验证。离散元法允许岩块之间滑动、平移、转动和岩体断裂等复杂过程,具有宏观上的不连续性,可以较真实、动态地模拟边坡块体在开挖过程中应力、位移和变形状态的变化特征以及岩体破坏过程[10]。具体方法可以参考相关文献[11-12],下面列出其相关的计算分析要点:
(1)运动方程:将块体离散化为有限差分三角形,网点由三角形的顶点组成,每个网点的运动方程为:
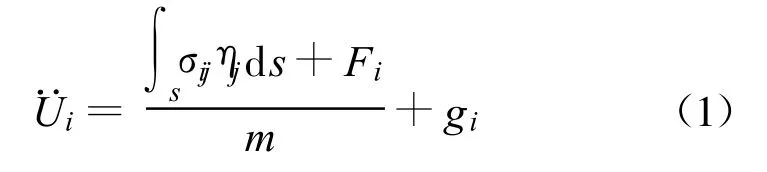
式中:¨Ui为网点i的运动加速度;σij为应力张量;s为包围块体集中的网点的面;ηj为s面的单位法向矢量;Fi为作用于网点i的外部荷载;gi为i点的重力加速度;m为岩块的质量。
(2)求解过程:单元受节理等不连续面的控制,在以后的运动过程中,单元节点可以分离,即一个单元与其临近单元可以接触,也可以分开。将求解空间离散为离散元单元阵,并根据实际问题用合理的连接元件将相邻两单元连接起来,单元间相对位移是基本变量单元之间相互作用的力,可以根据力和位移的关系求出,而个别单元的运动则完全根据该单元所受的不平衡力和不平衡力矩的大小按牛顿运动定律确定。从而得到所有单元在任意时刻的速度、加速度、角速度、线位移和转角等物理量。
2.2 模型建立
建立3DEC计算模型,模拟实验平台中的水泥砂浆试块,模型尺寸为:x方向80 cm,y方向50 cm,z方向110 cm。计算中节理为贯通平直节理,两组节理的性质相同,被节理切割的岩体为符合Mohr-Coulomb准则的弹塑性可变形块体。
2.3 变形参数和力学参数的选取
变形参数主要为杨氏模量E和泊松比ν,强度参数主要为粘聚力c和摩擦角φ。由于E和ν不能有效的反映材料的力学行为,如变形等[13]。因此,采用体积模量(K)和剪切模量(G),计算如下:
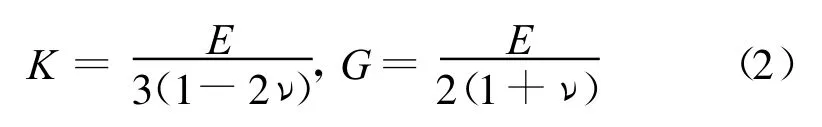
节理岩体中要求输入节理面法向刚度Kn,节理面剪切刚度Ks,以及粘聚力c,摩擦角 φ,抗拉强度T等参数见表3、表4。

表3 岩体力学参数取值

表4 结构面力学参数取值
2.4 计算过程及结果分析
模拟块体滑落时模型试验平台中旋转角按照10°为单位在0°~80°之间模拟块体的滑落过程。旋转角为α=0°时的计算块体的滑落过程如下(图4),当倾斜角β=0°时,楔形块体处于稳定状态,而当倾斜角 β=31°时,楔形块体开始滑落,此时,取 β=31°为块体滑落的临界角。

图4 α=0°时块体的滑落过程
计算过程中在楔形块体内设置一固定点,用以监测块体滑落时的速度,图5为楔形体内一点Y方向的速度随计算时步的变化图。从图5中可以看出,楔形块体的速度基本上趋于0,说明此时块体是稳定的,没有发生滑落破坏。逐渐增加倾斜角,当 β=31°时,从图6速度变化图中可以看出,该点的速度出现上下波动的不稳定变化,说明楔形块体开始滑落。
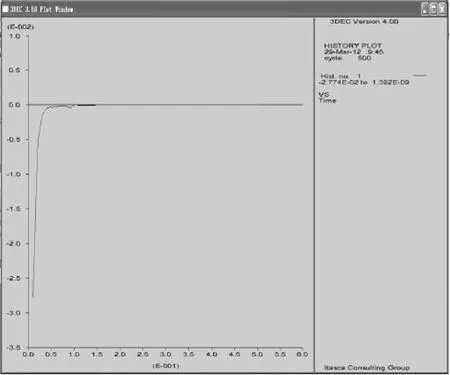
图5 β=0°时关键块体中速度随时步变化的曲线

图6 β=31°时关键块体中速度随时步变化的曲线
按照上面的模拟方法,分别模拟实验平台的倾斜角 α为 10°,20°,30°,40°,50°,60°,70°,80°时 ,块体的滑落过程,并记录楔形块体开始滑落时平台的倾斜角。
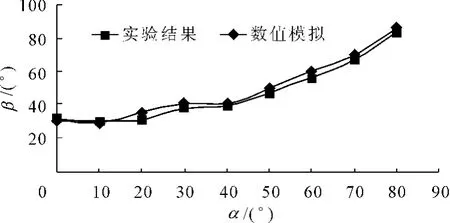
图7 块体滑落模型实验与数值模拟比较
数值模拟结果与平台模型实验结果显示(图7),旋转角 α为0°,倾斜角 β 为 31°时,楔形块体开始滑落,其余角度旋转角的数值模拟结果相差在5°以内,分析其原因一方面是由于模具模型浇筑出的模块表面是粗糙的,这就为试块提供了不确定的咬合力,另一方面已经浇筑好的模型无法提供其内摩擦角和粘聚力,总体上结果基本一致,说明实验结果的合理性。
3 结 论
本文利用自行开发的实验平台和三维数值方法主要研究了边坡开挖过程楔体的滑落过程,从实验和数值分析角度,分析了实验平台在不同的旋转角和倾斜角时对块体滑落的影响,研究结论如下:
(1)选用大理岩和水泥砂浆的试块进行实验,水泥砂浆表面粗糙,楔形块体滑落时的倾斜角度略大于大理岩的倾斜角度,而且当旋转角处于40°~50°之间,楔形块体滑落时的角度变化较大,因此,认为楔形块体双面滑落与单面滑落的分界角度在这个区间。
(2)实验结果与数值模拟的结果计算基本一致,在实验过程中存在一定的误差,导致数值模拟的假定与实验不能完全相符,总体上结果验证了实验过程的合理性。
[1]于青春,薛果夫,陈德基.裂隙岩体一般块体理论[M].北京:中国水利水电出版社,2007.
[2]王国新,徐令宇.自由场地液化振动台实验结果分析与数值模拟[J].防灾减灾工程学报,2010,30(增):45-49.
[3]刘明贵,岳向红,杨永波,等.岩石锚杆拉拔实验的数值分析[C]//第二届全国岩土与工程学术大会论文集.武汉,2006.
[4]赵 文.块体理论中关键块滑落的概率分析[J].中国有色金属学报,1998,8(2):356-359.
[5]陈祖煜,汪小刚,杨 建,等.质边坡稳定分析——原理·方法·程序[M].北京:水利水电出版社,2005.
[6]张 航,王述红,郭牡丹,等.岩体隧道三维建模及围岩非连续变形动态分析[J].地下空间与工程学报,2011,8(1):43-47.
[7]王 隽.块体理论分析与软件开发[D].上海:同济大学,2009.
[8]韩 梅.块体理论在边坡稳定分析中的应用[J].西北水电,2009,(5):13-16.
[9]王彦东.岩质高边坡关键块体的确定及稳定性评价研究——以汤屯高速公路为例[D].成都:成都理工大学,2007.
[10]孙 宁,杨文柱,姜清辉.三维块体分析方法及有效性验证[J].中国水运,2007,5(9):127-129.
[11]刘锦华,吕祖晰.块体理论在工程岩体稳定分析中的应用[M].北京:水利电力出版社,1988.
[12]王述红,张靖杰,李云龙,等.工程岩体开挖过程全空间块体搜索及其系统研制[J].东北大学学报(自然科学版),2010,31(7):1026-1029.
[13]周正义,曹 平,林 杭.3DEC应用中节理岩体力学参数的选取[J].西部探矿工程,2006,18(7):163-165.
