优化教育投入以促进经济发展的实证研究

王敬华

（天津市红桥区职工大学 天津 300131）

“坚持教育优先发展”是我国现阶段的教育方针，然而，2012年我国教育经费投入达到GDP的4%，却仍然低于世界平均水平，我国财政收入增长缓慢，而教育经费大部分来源于财政，面对资源的“稀缺性”，是搞好经济建设，还是进一步增加教育经费投入？教育经费投入是如何促进经济发展的？有限的教育经费投入，如何才能更好地进行分配？本文将利用实证方法，对以上问题进行探讨。

一、教育经费与人均GDP的VAR模型

VAR模型又称向量自回归模型，它并不通过经济学理论，而是通过时间序列进行模型建立，将有相互关系的变量包含到模型中，进而确定滞后期k，从而使模型反映出变量之间相互影响的绝大部分。本文选取近20年的教育经费投入和人均GDP作为相互影响的两个变量。

1、格兰杰因果检验

遵照数据处理原则，为了消除模型异方差，我们在建立模型前对教育经费和人均GDP两个变量进行取对数处理，同时可使变量关系更加线性化。

运用Eviews软件进行格兰杰因果性检验，通过尝试，进行滞后期为4的格兰杰检验，在以0.05为显著性水平的条件下，使得检验结果为“INPUT does not Granger Cause GDP”（INPUT 表示教育经费），这时概率定义 P（F＞10.13）=0.25落在原假设接受域，这表明接受“教育投入不是GDP的格兰杰原因”；同时推翻“GDP does not Granger Cause Input”（P（F＞179.3）=0.052，接近临界值0.05）的假设检验，也就是说，在教育经费和人均GDP的因果关系中，人均GDP在VAR模型中占的重要性较高，影响未来教育经费投入。这个结论符合“经济基础决定上层建筑”的原理，同时说明“经济发展水平决定教育水平”。

2、数据模型的稳定性检验

图1

通过计算我们发现，原变量的特征根在单位圆外，因此VAR模型不具有稳定性。运用经济学原理，我们建立两个变量先取对数然后再进行差分的VAR模型，这样形成的新变量的可以将其看作原变量的增长率序列，其优势为通过VAR模型的建立，更好说明其中一个变量的增长速率的变化对另一变量的影响，在经济学的分析中更为常见，有利于我们进一步分析问题。

VAR模型的稳定性要求特征方程|A1-lI|=0的全部根必须在单位圆以内，用Eviews软件分析新的时间序列得到两对共轭复根，每个根的模均小于1，通过图1看出所有根均在单位圆内，这就表明我们用新的变量建立的VAR模型是稳定的。VAR模型对稳定性的检验，其目的是保证变量变化的冲击对模型的影响会逐渐消失，这一假设条件的存在，才能使基于VAR模型的经济学分析具有实际意义，即任何经济内变量的变化对经济主体的影响不能无限制延续下去。

3、模型的脉冲响应分析

前面已经谈到，本文最终建立的变量反映增长率之间的关系，那么，对于图2而言，当教育投入增长变化1个单位量时，对人均GDP的影响将滞后在一个时期以后，也就是说，在第2期开始，人均GDP反方向变化1%，但在第3期开始有个折点，表明这种变化从第3期开始减弱，从第4期开始，这种影响变为正向促进作用，在第7期达到峰值后逐渐消失。因此我们可以认为教育经费投入的增长对经济在初期有一个挤出效应，并且这个挤出效应将滞后1个时期，然后持续2个时期后会消失。

类似的，图3表示人均GDP的增长率变动一个单位的标准差时，教育经费投入增长率在当期就迅速做出反应实现同向增长，第2期的折点表明这种影响更大，第3期的折点表明影响逐渐减小，最终逐渐消失。

脉冲响应分析的结论是：经济增长和教育经费投入这两个变量的影响是相互的，当经济增长率增加时，对教育经费的增长是正面的，迅速的，教育经费投入会随之增加，但这种增加首先反映出的是经济的挤出效应，教育投入对经济增长的正影响需要至少3个时期才能显现出来；同时经济增长还可以视为教育直接或间接产出，这样我们就可以进行下文的工作，即将相互作用的两个变量中的教育经费投入作为经济发展的自变量进行模型建立，从而进行教育资源的合理配置，促进经济增长。

二、教育生产函数的建立

1、教育生产函数的提出

经济学认为，国民产出主要与劳动力数量、资本投入量以及土地数量有关，而在当期土地数量不断减少，土地的产出相对于国民经济而言的影响越来越小，因此，将经济增长水平由函数Y=f（L，K）表示（其中L表示劳动力数量；K表示资本投入量）。假定国内生产总值Y与劳动力L和资本K之间的关系满足柯布一道格拉斯生产函数的形式，即：

这里，α，β分别表示资本和劳动力的产出弹性，t为时间变量，r为技术进步系数，A0为常数，表示基年技术水平。

为了进一步进行最小二乘法分析，对公式（2）两边同时取对数，得到：

图2

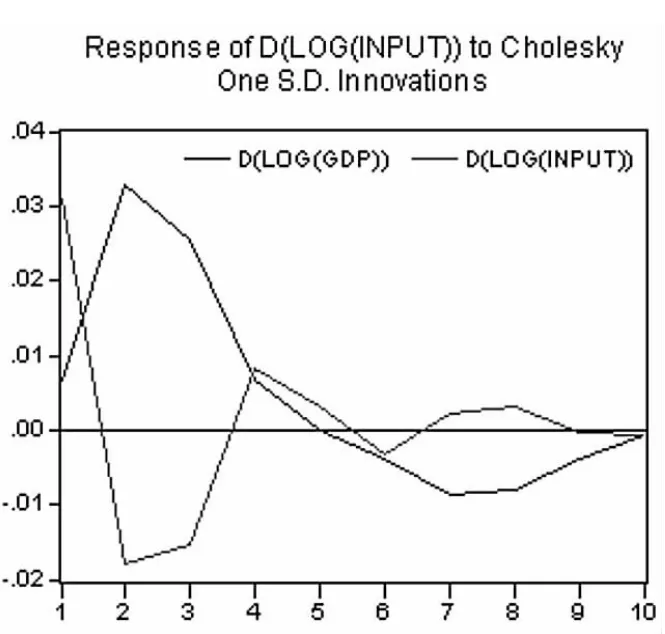
图3

考虑到国民生产总值的取得取决于两项投资，一项是资产投资，一项是人力资本投资，而教育投资是人力资本投资的主要来源，这样我们将人力资本投资划分为初等教育、中等教育和高等教育三个阶段，从而可将生产函数转变为，为了深一步揭示人力资本投入对国民经济的影响，进一步忽略技术进步的影响，此时：

公式（3）的得出，主要基于柯布一道格拉斯生产函数，但是更加重视不同教育层次对经济增长的贡献和作用，本文将之称为教育生产函数。

2、教育生产函数参数估计

（1）指标的选取。对于因变量Y而言，能够反映经济增长水平的最普遍的指标就是GDP水平，因此采取人均GDP（元/人）作为教育生产函数的产出指标；对于固定资本投入K，本文选取人均社会固定资产投资（元/人）；对于教育资本投入L，考虑到前面教育经费与经济增长的VAR模型，教育经费投入可以在一定程度上说明经济增长水平，同时由于取得数据的局限性，因此本文分别选取小学L1，中学L2，和大学L3的人均教育事业费支出作为自变量指标，这一指标可以衡量在我国普遍提高劳动者受教育程度的力度，从一定角度反映人力资本水平。

（2）参数估计。为了更好地进行最小二乘法估计，本文同样参照生产函数对公式（3）进行处理：

最小二乘法的回归结果为：

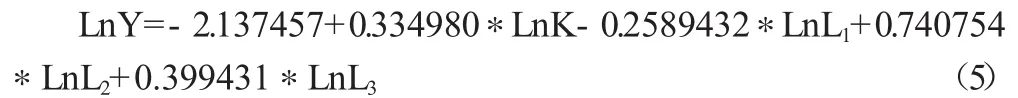
在这一结果中常数项和小学教育的DW值分别为-2.967830和-2.865042，小于2，表明不能通过杜宾检验，说明函数的变量之间存在着强烈的自相关现象，需要进一步优化模型。

通过不断修正，只有剔除小学教育投入和常数项，并修正自相关，才能通过杜宾检验，最终得到的回归模型为：

公式（6）进行了一阶自相关修正分析，各个自变量的DW值均大于2，基本消除了自相关现象，并且整个函数的拟合优度R2=0.992463非常接近1，所以模型的建立较为理想。

3、教育生产函数的结论

公式（5）说明，我国小学教育经费支出与人均GDP的经济产出关系不显著，并且呈负相关，这说明我国小学新入学人口已呈下降趋势，但是我国小学教育的人均投入依然呈快速上升趋势，以致对经济发展表现为抑制作用；公式（6）说明，中等教育的产出弹性大于高等教育，说明我国目前正处于中等教育发展水平，中等教育投资的增长对经济的促进效果更为明显。

三、政策和建议

1、重视教育对经济的作用

通过前面的VAR模型，我们首先了解到一个重要信息：经济增长时，对教育经费的影响是迅速的。从教育生产函数看，教育投资同社会固定资产投资相比，其产出弹性明显大于社会固定资产投资。这就要求我们从政策角度重视教育对经济的作用，这个重视作用不仅表现在当经济增长时，应通过政策建议我国各级各类政府保证教育经费投入持续增长，使其增长的力度至少不得低于地区GDP及政府运行经费增长比例；尤其当国民生产总值出现波动时，应警惕对教育投资可能出现的抑制作用，更应该充分贯彻“教育优先发展”原则，保持或适度提高教育经费的投入比例，从而维系国民经济发展的内在动力，切实实现科教兴国的战略目标。

2、关注教育投资对经济影响的敏感性

从VAR模型看，教育投资对经济发展具有滞后性，教育对科技进步的影响需要一个时间过程，教育对社会劳动力素质的影响也需要时间，所以，各级政府对于教育投入的作用应该更具发展眼光看问题。同时，要分析教育投资的脉冲响应分析，教育投资的增长在第4期才能对经济产生正方向的影响，第7期达到峰值，理想状态下的政策的制定应把握教育投资对经济影响的敏感性，也就是说，在我国教育投资水平低于世界平均水平的前提下，教育投资的增速控制应通过科学计量并且不是一成不变的，要在教育对经济增长的作用有所衰退时提前进行政策改变，使其能够契合对经济影响的脉冲影响效果，保持持续的增长效应。

3、把握教育发展水平，优化教育经费投入

我们应该看到，教育投资水平的增速需要一个逐渐增加的过程，才能既保持经济增长速度，又持续提高教育水平，因此，面对目前我国教育投资整体水平偏低，通过实证分析把我国教育水平定义在“中等发展水平”就显得尤为重要。我国一贯重视的九年义务教育中，对于其中的小学部分，是教育的基础，虽然重要，但是在教育生产函数中却表现为负相关，因此应降低教育投资的增长速率，保持其稳定发展；而教育中的中等教育，在教育生产函数中占据较大的份额，应适度增加其教育投资，以提高对经济增长的促进作用；对于高等教育，关系到国民素质的整体提高，科技型社会的内涵式发展，在经费不足的现状下，更要重视资金的合理运用，避免学科重复性建设和资金浪费，努力提高高等教育软实力，合理优化教育经费的投入，全面促进经济发展。

[1]吴云勇：中国教育经费与国民经济增长的适应度分析[J].教育学术月刊，2010（10）.

[2]郭甲蕾、肖骞、李俊江：我国财政性教育经费投资与经济增长的关系[J].中国外资，2011（6）.

[3]薛海平：中国西部教育生产函数研究[J].教育与经济，2008（2）.

[4]张志耀、梁嘉骅、芦彩梅：教育投入产出生产函数分析[J].管理工程学报，2000（1）.