一种PSK/QAM数字调制方式识别方法*

杨 敏,王金庭,朱 静

(1.中国地质大学（武汉）机电学院，湖北，武汉，430074；2.湖北经济学院 电子系，湖北，武汉，430502；3.中国地质大学（武汉）计算机学院，湖北，武汉，430074)

近年来，在无线广播、卫星通信、蜂窝移动通信等无线通信领域中，PSK和QAM两类调制方式得到了广泛应用。这两大类调制方式都是用不同的相位或联合相位及幅度来表示不同的符号，而星座图可以反映信号的相位和幅度特征,可用于信号分类[1]。Mobasseri[2-3]提出利用信号星座图形状作为判决的标志，该算法扩展性好，但是聚 类计算 复杂 。 Swami[4]、Hsiao-Chun[5]、Orlic[6-7]和田上成[8]等研究了高阶累积量值的调制识别方法，这些研究表明，高阶累积量相对于高阶矩具有抑制高斯噪声优点，适合用于信号调制类型的分类，但对于星座图相同的子类，用高阶累积量无法将其分类。

本文首先基于星座图对 BPSK、QPSK、OQPSK、UQPSK、π/4-QPSK、8PSK、方形 16QAM、星形 16QAM、16APSK、32APSK等信号的星座特征进行分析，然后给出基于高阶累积量以及信号差分后的高阶累积量进行信号调制识别的特征值构造方法，最后给出算法流程，并分析仿真结果。

1 常用数字相位调制信号及其星座图

MPSK信号的星座图为单位圆上均匀分布的M个点。OQPSK是QPSK的一种改进形式，其正交支路码元与同相支路码比在时间上偏移了一个比特间隔Tb。两信号的星座图完全一样，但差分后，QPSK信号星座图有9种位置点，而OQPSK信号星座图只有5种位置点 （如图1所示)。

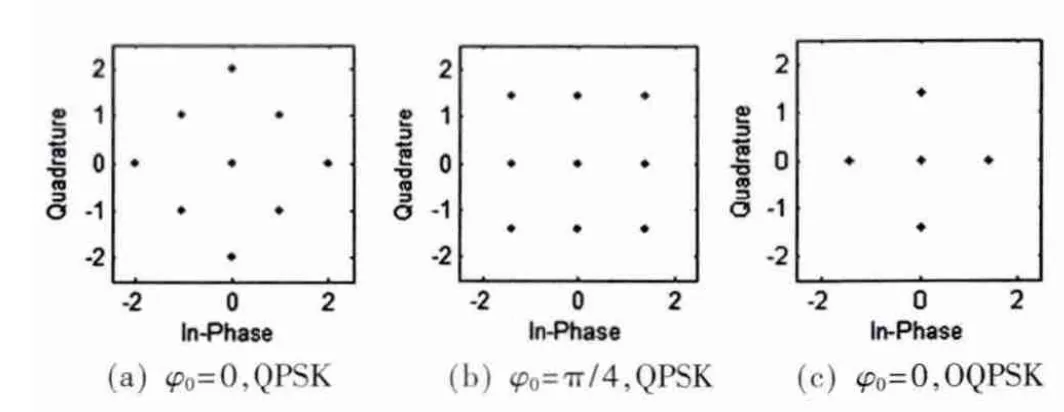
图1 QPSK信号与OQPSK信号差分后星座图

UQPSK信号通过对QPSK载波的两个正交分量分配不同的功率，来同时传输两种不同类型及速率的数据流。QPSK信号的星座图为正方形的四个顶点，随着非均衡因子的增大，UQPSK星座图对应的 4个点界定的正方形长变长，宽缩短，逐渐压缩。

π/4-QPSK信号是由两个相差π/4的QPSK星座图交替产生的，其星座图与8PSK信号的星座图相同。差分后的π/4-QPSK信号星座图上有16个位置点，而差分后的8PSK信号星座图上有33个位置点（如图2所示）。

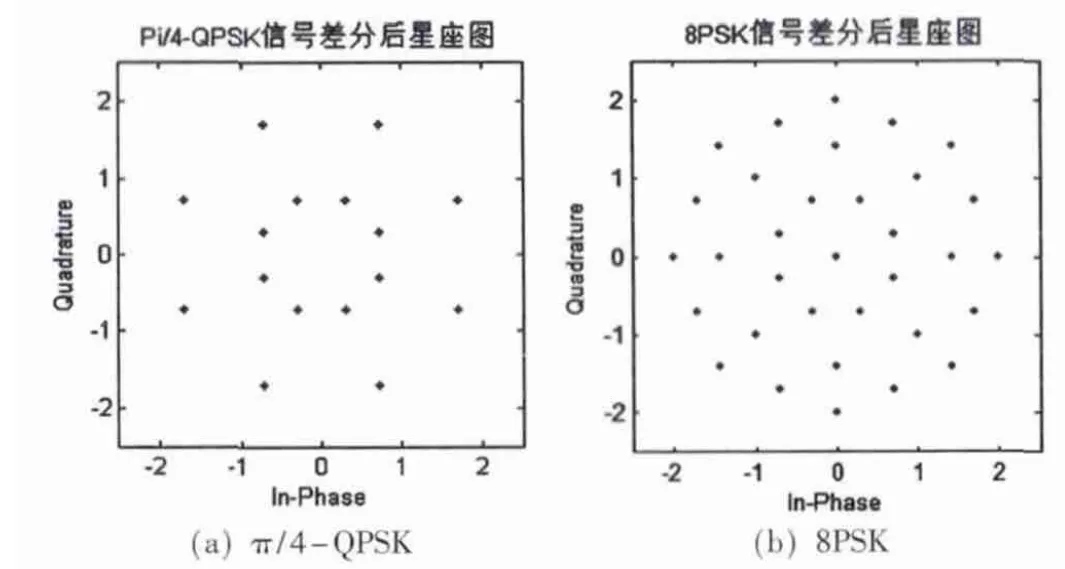
图2 π/4-QPSK与 8PSK信号差分后星座图

方形16QAM信号的星座图位置点的分布成方形，星形16QAM星座图的位置点分布成星形。星形16QAM仅有8种相位，两个振幅，而方形16QAM有12种相位，3个振幅。

M-APSK星座图由n个同心圆组成，每个圆上等间隔均匀分布PSK星座点。DVB-S2标准中，16APSK调制方式由2个同心圆构成，圆上星座个数各为 4和12。16APSK调制星座内环半径为R1，外环半径为 R2，内外半径比率(γ=R2/R1)有5 种,分别是 2.57、2.60、2.70、2.85和3.15。

DVB-S2的32APSK调制方式是由3个PSK同心圆构成，圆上星座点数各为 4、12和 16，其内环、中间环、外环半径分别为R1、R2和 R3。表1列出了 3个半径之间的 5 种比率(γ1=R2/R1，γ2=R3/R1)。

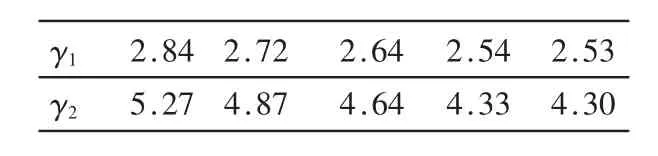
表1 32APSK内外半径比率

2 特征值的构造

高阶累积量能很好地表征信号的星座图分布情况，同时高斯白噪声大于二阶的高阶累积量的值为零，因此采用高阶累积量对信号进行分类具有很好的抗噪声性能。对于复平稳信号X(t)，其高阶累积量表示为[9]：

通过式(1),并用时间平均代替统计平均,可求得PSK、QAM各子类信号的高阶累积量。为避免接收信号的平均功率对识别的影响，采用高阶累积量的4种比值(F1=|C40|/|C42|，F2=|C41|/|C42|，F3=|C63|/|C42|3/2，F4=|C80|/|C42|2)作为分类特征。一些常用的PSK、QAM子类信号高阶累积量特征值如表2所示。

QPSK与OQPSK信号的高阶累积量特征值完全相同，π/4-QPSK与8PSK信号也是如此。将信号差分后再计算高阶累积量，并计算特征值，如表3所示。

由表3可知，采用特征值DF4可将识别QPSK与OQPSK信号，同样也可识别8PSK和π/4-QPSK信号。

BPSK信号与UQPSK信号的各个高阶累积量特征值都相差不大，用这些特征值分类识别效果不好。观察这两子类信号的星座图，BPSK星座值点离两分量坐标轴(I分量和 Q分量)的理论距离一个为0，另一个为 1，分别计算星座值点离两坐标轴的距离的最大值，然后计算两最大距离的比值L(大的除以小的)，此距离比是一个较大的数值。而UQPSK信号星座值点离两分量坐标轴距离比值的理论值在之间。利用这个特征值L可以有效地对此两子类信号进行分类。

3 算法流程及仿真结果

基于高阶累积量和星座图的调制方式识别算法流程如图3所示。

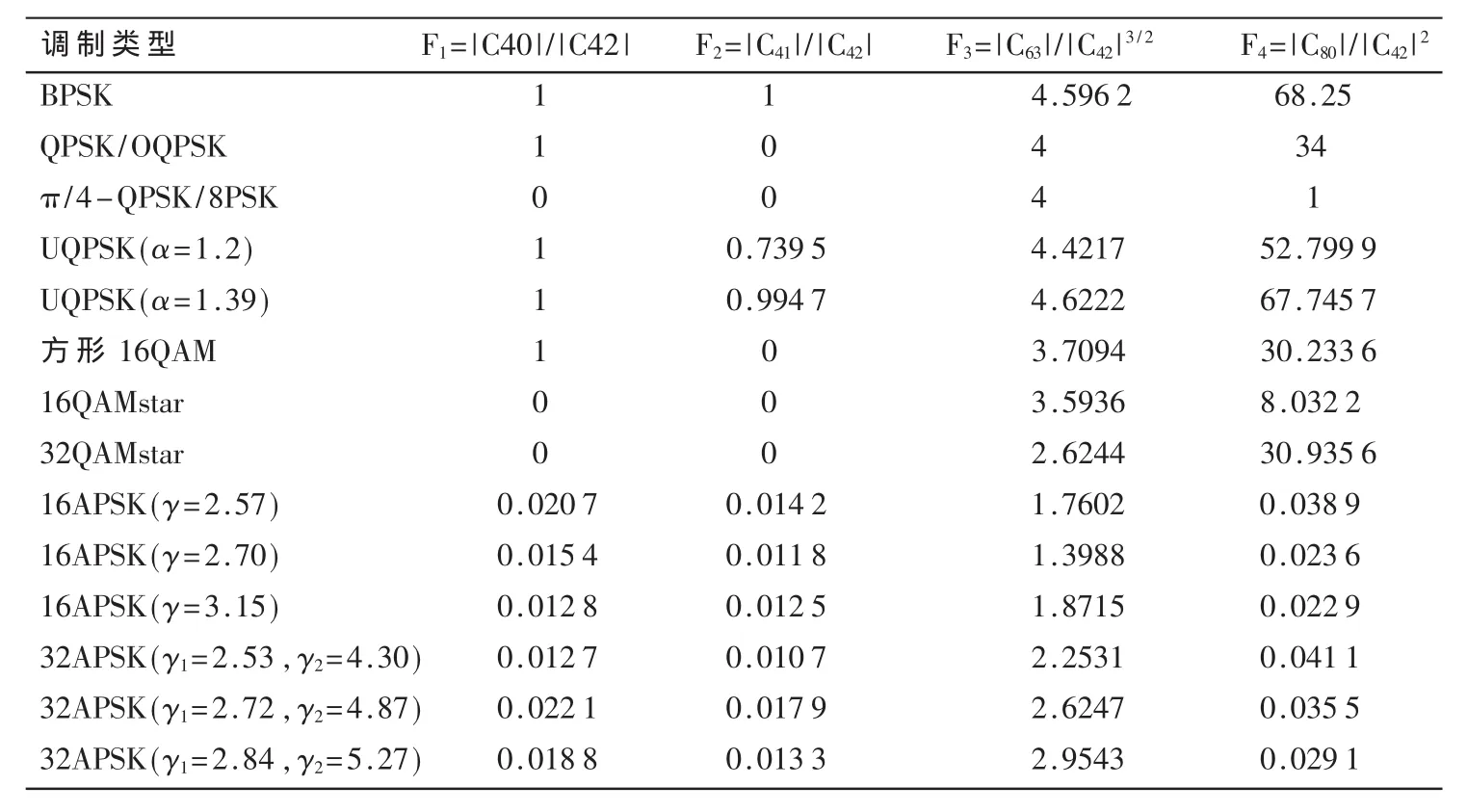
表2 PSK、QAM子类信号高阶累积量特征值

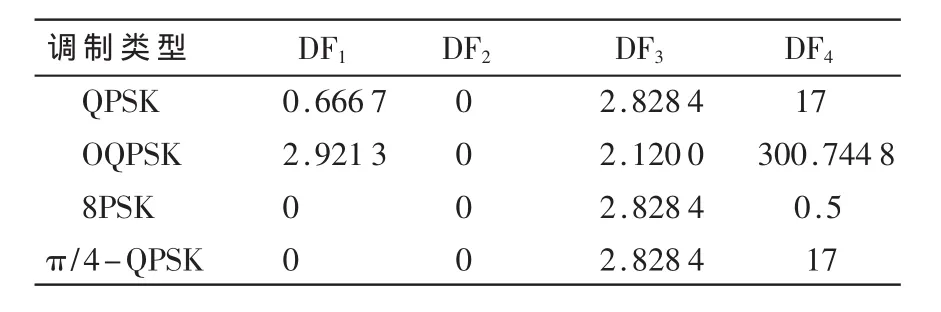
表3 信号差分后的高阶累积量特征值

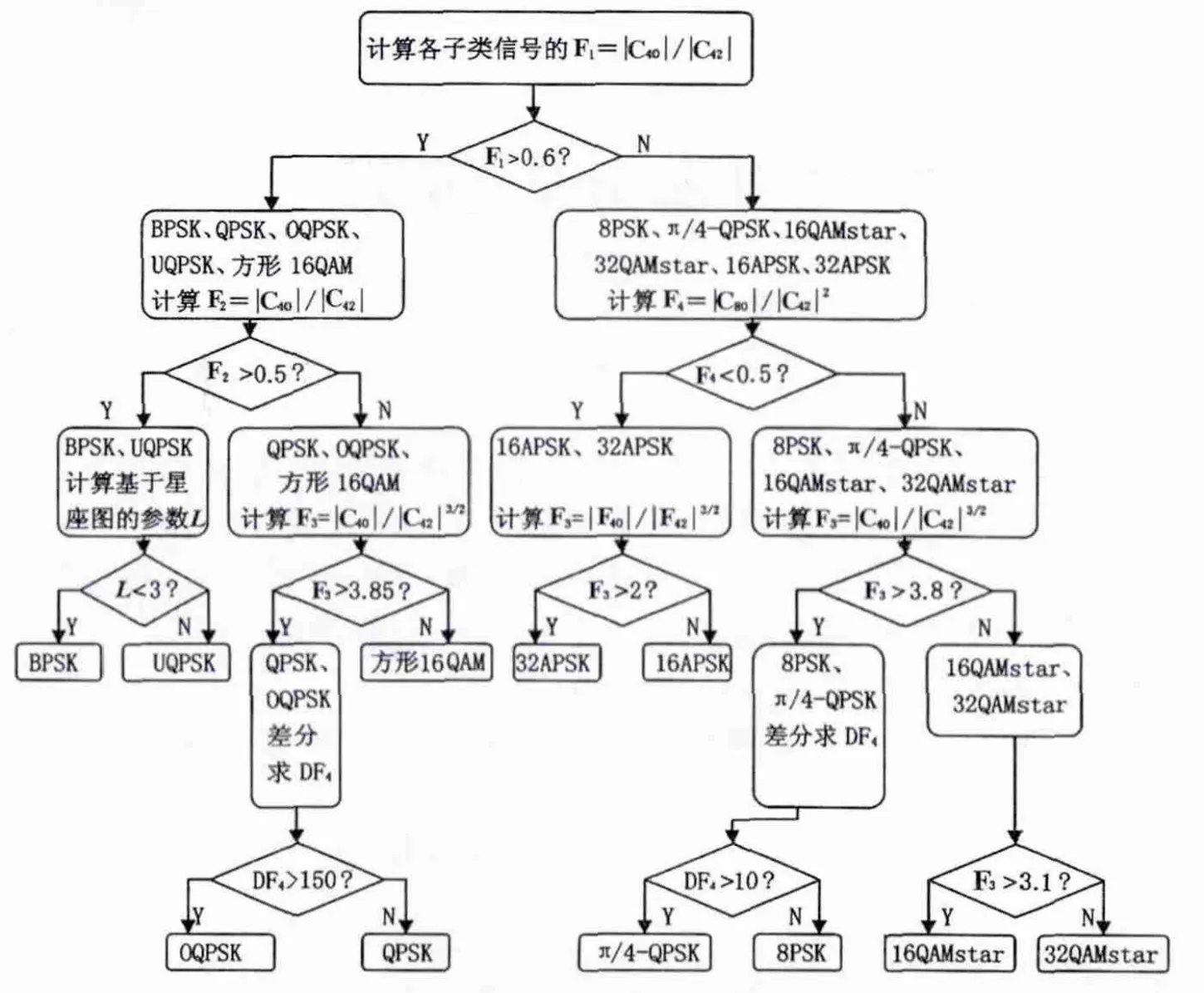
图3 基于高阶累积量和星座图的调制方式识别算法流程

仿真时，输入符号数Len=10 240，载波频率为符号率的2倍，采样速率为载波频率的8倍，在不同信噪比下对各种调制信号的正确识别次数和错误识别次数进行了大量的测试，各类信号的识别率曲线如图4所示。

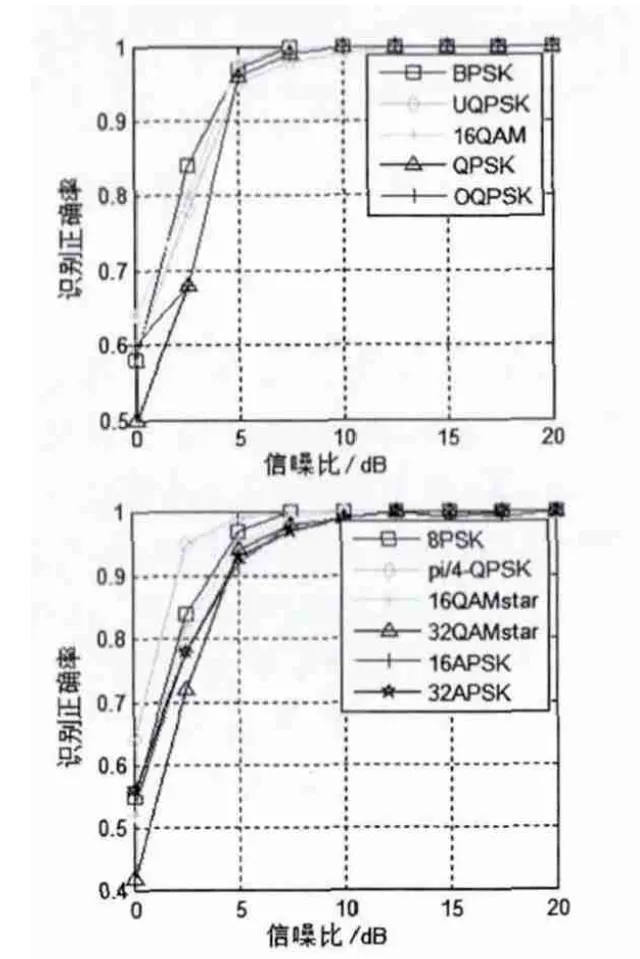
图4 各类信号的识别率曲线

仿真结果表明，在SNR为3 dB时所有信号的正确识别率均达90%以上，随着SNR的增加，识别率也相应地增加，到SNR为 5 dB时，识别率均达94%，到SNR为10 dB时，识别率均达99%。

本文针对常用PSK和QAM子类信号的调制识别问题，提出了一种基于高阶累积量和星座图的识别算法对PSK和QAM调制各子类信号进行识别。本文算法不需要精确同步，在较低信噪比下也能达到较好的识别性能。

[1]SHAHMOHAMMADI MOHAMMAD.Modulation classification for QAM/Psk using a soft clustering algorithm[A].ISIT，2002,19.

[2]MOBASSERI B G.Digital modulation classification using constellation shape[J].Signal Processing,2000,80(2):251-277.

[3]MOBASSERI B G.Digital modulation classification using constellation shape[EB/OL].//www.yahoo.comsearchmodulation classification.

[4]SWAMI A,SADLER B M.Hierarchical digital modulation classification using cumulants[J].IEEE Transactions on Communications,2000,48(3):416-429.

[5]WU H C,SAQUIB M,YUN Z F.Novel automatic modulation classification using cumulant features for communications via multipath channels[J].IEEE Transactions on Wireless Communications,2008,7(8):3098-3105.

[6]ORLIC V D,DUKIC M L.Automatic modulation classification algorithm using higherorder cumulants under realworld channel conditions[J].IEEE Communications Letters,2009,13(12):917-919.

[7]ORLIC V D,DUKIC M L.Multipath channel estimation algorithm for qutomatic modulation classification using sixthorder cumulants[J].Electronics Letters,2010,46(19):1349-1349.

[8]田上成,王可人,金虎.卫星通信中数字调相信号调制方式识别方法研究[J].信号处理，2012,27(2):271-275.

[9]张贤达．时间序列分析—高阶统计量方法[M]．北京：清华大学出版社，1996．