电力线通信中OFDM同步改进算法研究

谢志远，罗 蕾

(华北电力大学电气与电子工程学院，河北 保定 071003)

责任编辑:薛 京

随着我国智能电网建设的不断深入，电力线通信技术已经成为支撑智能电网建设的重要技术之一，为了提高电力线通信系统的传输速率和可靠性，电力线通信中需采用合适的调制解调方案。正交频分复用技术是一种高效调制和多载波传输的技术，其频谱利用率高，且能有效地对抗电力线载波通信存在的频率选择性衰落、多径和各种噪声［1－2］。但OFDM对系统的频偏和定时误差敏感，对各子载波之间的正交性要求也十分严格，微小的频偏都会破坏子载波之间的正交性，从而引入ICI(Inter－Channel Interference)信道间干扰，这将导致OFDM系统的性能急剧恶化，若将频偏以子载波间隔为单位，其可分为整数部分和小数部分［3］，整数部分的频偏不会产生ICI，其影响表现为输出子载波循环移位，小数部分的频偏将会引起ICI［4］。当OFDM系统中存在定时误差，就会导致数据相位旋转，从而形成ISI(Inter－Symbol Interference)符号间干扰。因此，在OFDM中准确的符号定时和频偏估计是一个关键的问题。

对于OFDM的同步问题，不少研究学者均提出各自的解决方法，文献［4］中Schmidl提出S＆C算法，此算法使用2个训练序列，第1个用来完成OFDM符号定时和小数频偏估计，第2个完成整数频偏估计，但是由于循环前缀的影响，符号定时的估计曲线存在平台效应，使得符号定时不够准确，从而影响频偏估计。文献［5］中Minn针对S＆C算法的不足提出一种改进的定时算法，其使用的训练结构与前者不同，该方法的优点是定时测度曲线具有尖峰。但其仍存在多个副峰，有时错误时刻的峰值也会超过正确时刻的峰值，这将影响定时同步的准确性。文献［6］中为了克服文献［4－5］中出现问题，Park提出一种训练符号结构，使测度曲线具有尖峰，但是在低信噪比或信道复杂的情况下，Park定时估计测度曲线会出现侧峰或者峰值过小的情况，从而影响符号定时同步。在电力线信道中，由于其信道的固有特点(频率选择性衰落、多径及富含噪声)，上述3种方法应用到电力线信道中同步精确度均比较低。

通过分析电力线信道和OFDM系统的模型，本文采用CAZAC序列为训练序列的OFDM系统时频同步算法，该算法使用一个训练序列能同时完成符号定时和频偏估计。仿真表明，改进的算法克服了文献［4－6］中存在的问题，在电力线通信中OFDM符号同步更加精确，在此基础上频偏估计更加准确，算法更加稳定可靠。

1 电力线信道模型

当用电力线信道传输高频信号时，会出现多种衰减，但主要包括两种衰减:耦合衰减和线路衰减。一般耦合器的内阻可以做得非常小，所以信道的衰减主要由线路衰减决定。本文将从下面两个方面来分析考虑线路衰减:多径传播造成的频率选择性衰减和线路损耗衰减。通过对单分支结构的线路模型分析获得电力线信道模型，单个支路的传输模型如图1所示。

图1 单分支信道传播模型

信号由点A传送到点C，在点B处有一分支BD，传输线路由AB，BC和BD三段组成。为简化分析，假设点A和点C与线路的阻抗相匹配，三段的长度分别为L1，L2和L3，相应的阻抗为Z1，Z2和Z3，r为反射因子，t为传输因子。信号从点A传送到点C存在多种可能性:A→B→(D→B)(N－1)→C，其中N为整数且N≥1，路径的衰减由衰减因子gi表征，其为反射因子和传输因子的乘积，因电力线信道中反射因子、传输因子的值均为小于1的数，所以传输距离越长，gi的值越小，线路衰减越大。路径延时为τi=di/vi，τi为第i条路径的延时，di指路径i的长度;vi=c0/，c0为光速，εr是PVC绝缘材料的介电常数。综合每条线路自身衰减及信道多径造成的衰减、延时，得到多径信道的传递函数为

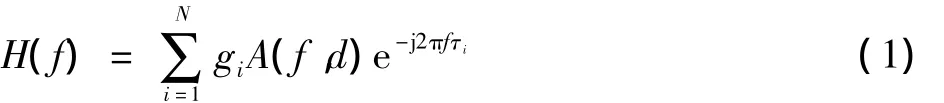
式中:A(f，d)为电力线信道用来传输高频信号时线路的损耗衰减，根据传输线理论推导可知A(f，d)=e－(a0+a1fk)d，即信道的传输函数可表示为

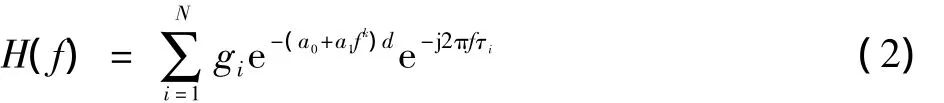
式中:a0，a1为衰减参数。

本文仿真信道采用如图1所示的单分支线路电力线信道，并假设点A和点C阻抗与线路的阻抗相匹配，点D开路，即r3D=1。线路的衰减参数和多径衰减参数如表1、表2所示。

表1 线路衰减参数

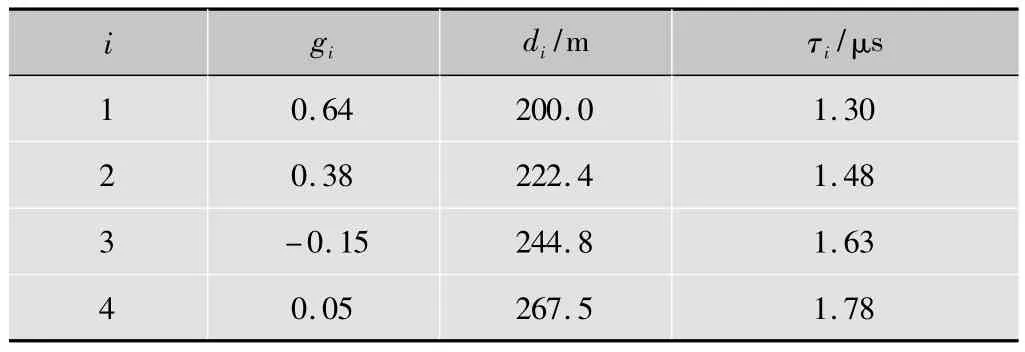
表2 多径衰减参数

利用表1和表2中的数据，通过仿真工具可以得到信道的频率响应和脉冲响应如图2所示。

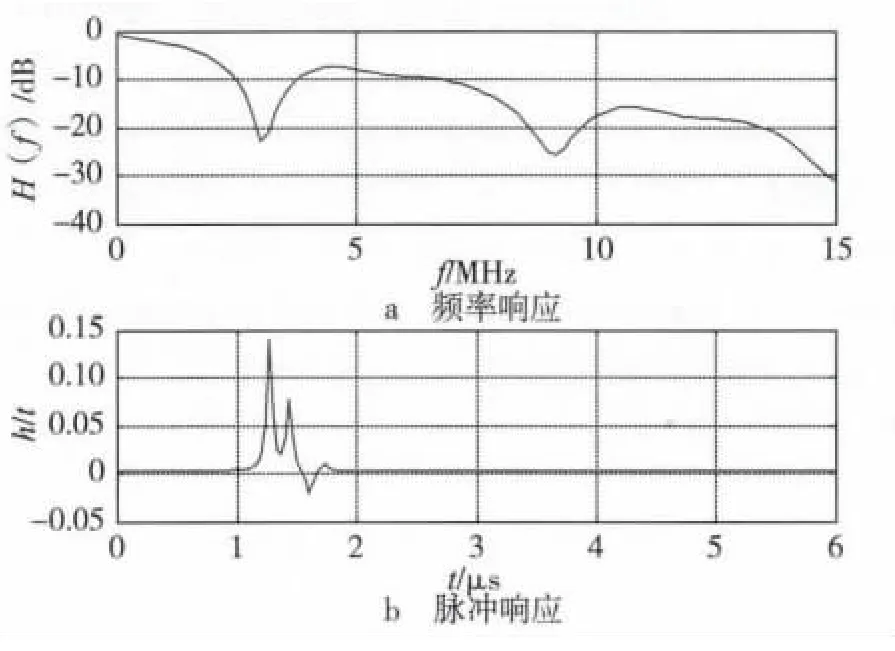
图2 信道的频率响应和脉冲响应

2 OFDM系统

图3所示为一个典型的OFDM传输系统，信号经过信道编码、交织、信号映射、插入导频信号之后进行串并变换，通过N点IFFT计算之后，信号从频域变化到时域，再经过并串变化。为了避免ISI，将在数据的前部添加长度为Ng个点循环前缀，构成长度为N+Ng的OFDM数据。信号通过信道之后，经过定时和频率同步模块，估计出符号定时和频偏，去掉循环前缀，经过FFT变化后，再通过信道估计以及一系列的反变换恢复数据。

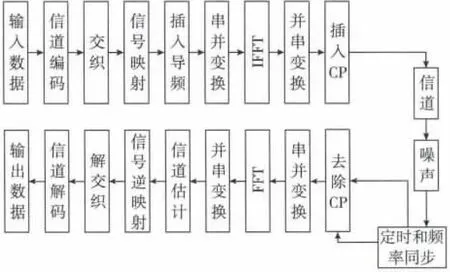
图3 信道的频率响应和脉冲响应

OFDM系统中，OFDM时域信号的表达式为

式中:N为系统子载波的个数;X(k)为第k个子载波上调制的复数据。加入循环前缀之后，OFDM符号可表示为［x(N － Ng)，…，x(N － 1)，x(0)，x(1)，…，x(N －1)］，信号经过信道传输，信号受到噪声和频率偏移的影响，接收端和发送端的定时以及载波频率会产生偏差，接收端的信号表示为

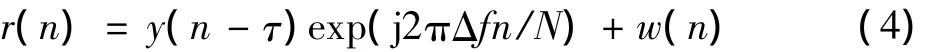
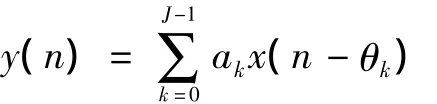
3 同步算法

对于文献［4－6］的算法中存在的问题，究其原因是因为循环前缀是训练序列的复制，循环前缀与训练序列有较强的相关性。电力线通信中信道情况复杂，采用不合适的同步方法将使OFDM系统同步性能急剧下降。为了提高电力线信道中定时估计的准确度，需要改进定时测度的曲线，使其只出现唯一的尖峰且不出现副峰。相对于文献［4－6］算法，本文算法训练序列使用的是CAZAC序列，且改变训练序列结构，增加定时测度函数的计数点。

长为Nc的CAZAC 序列［7］μ(k)满足

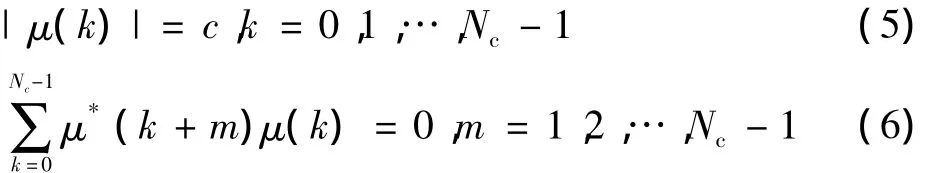
CAZAC序列经过FFT/IFFT变换之后仍然为CAZAC序列。根据文献［7］取CAZAC序列为

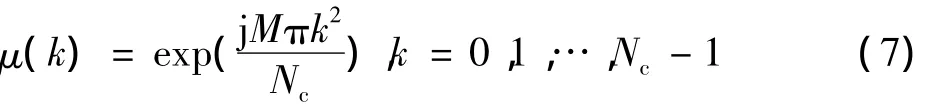
式中:M为正整数，且M与Nc互质。

本文中采用的训练符号的结构为ST=［AN/4，BN/4，AN/4，－BN/4］，其中N为子载波的个数，M取值为1，Nc取值为N/2 ，BN/4(k)=AN/4(k)V(k)，k=0，1，…，N/4 －1 ，AN/4(k)=V(k)= μ(k)。

改进的算法符号定时估计是通过寻找相关函数的最大值来完成的，根据ST的结构定义相关函数为

式中:

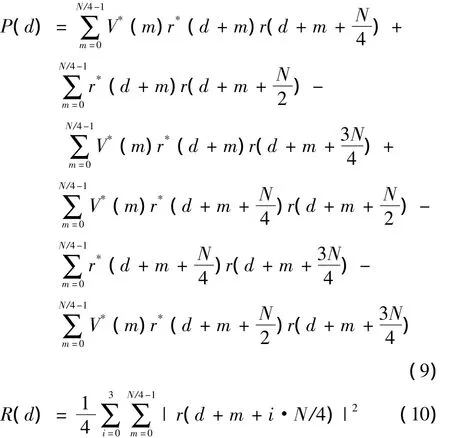
相比于文献［4－6］中的算法，改进的算法通过增加P(d)，R(d)的计数点，在正确的定时时刻，每个相关运算值都最大，多个叠加使正确符号定时峰值凸显并削弱非正确符号定时的影响。且由于CAZAC序列具有恒定的包络和良好的自相关性质，这就减小了循环前缀对符号定时估计曲线的影响。

估计出定时同步位置之后，在时域中确定符号的起始位置，根据ST结构求小数频偏，定义

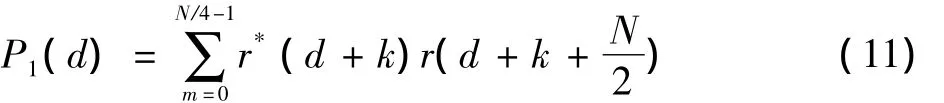
则归一化小数频偏估计为

由式(12)可知，小数频偏估计范围为［－1，1］。

进行小数频偏补偿之后，频偏中只含有整数频偏。设经小数频偏补偿之后的信号为r1(k)，则定义

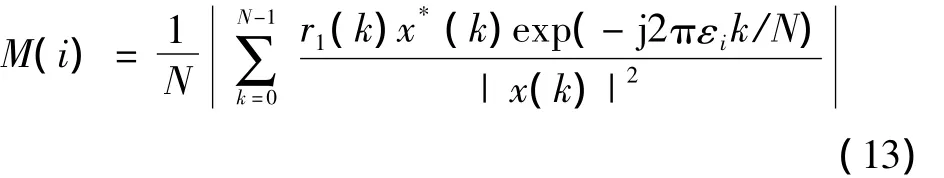
式中:εi= － N/2，－ N/2+1，…，0，1，…，N/2 － 1，N/2 。从式(13)可知，εi越接近整数频偏时，M(i)值越大，当εi达到整数频偏的值时，M的值达到最大，即在式(13)中得到最大相关值的移动位置，从而得知整数频偏为

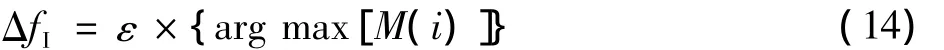
归一化整数频偏的估计范围是［－N/2，N/2］。

4 仿真分析

为了验证本文算法在电力线载波通信中OFDM同步的准确性，在MATLAB中对该算法进行仿真分析。电力线信道选用上述所分析的电力线信道，电力线信道的随机噪声采用加性高斯白噪声模拟，OFDM电力线通信仿真参数如下:基带时钟为200 kHz，子载波N=128，循环前缀Ng=32，子载波间隔为1.562 5 kHz，OFDM 符号的总点数为160，频率偏移为14.5。对10 000个OFDM帧进行仿真。

电力线信道下，信噪比为5 dB时S＆C算法、Minn算法、Park算法及改进算法的符号定时测度曲线如图4所示。从图中可以看出，由于CAZAC序列具有尖锐的自相关峰值和零旁瓣的特性、改进的ST的结构和P(d)的计算点增多，在电力线信道中改进算法的定时测度曲线只有一个尖锐的峰值，且避免了S＆C算法在整个循环前缀上的平台效应、Minn算法的多峰现象。图中可明显看出在电力线信道中，S＆C算法的定时测度曲线图基本上已经失去正确估计正确符号位置的能力，Minn算法中仍然存在副峰的现象，且其定时测度曲线的峰值远远小于改进算法的峰值。Park算法虽能正确地符号定时，但是它的峰值也小于改进算法定时测度曲线的峰值，并且它的定时测度曲线在距离正确的符号定时点N/4处有一个副峰，与主峰值相差不大，将会对系统的同步性能产生一定影响。

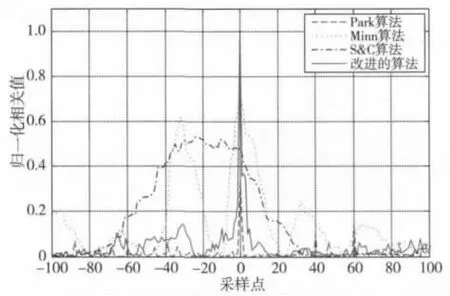
图4 定时比较

根据文献［6］可知，Park算法的符号定时性能优于S＆C算法和Minn算法，所以本文中只比较Park算法与改进算法的符号定时性能，通过估计均值和均方误差(MSE)大小来完成性能比较。不同信噪比的情况下，Park算法和改进算法仿真得到符号定时估计误差均值和MSE如图5、图6所示。从图中可以看出，在低信噪比的情况下，改进的算法具有较好的定时同步估计均值和均方误差，在信噪比大于－7 dB时就可以实现精确的定时同步，而Park算法应用在电力线信道中时，在整个仿真的信噪比范围内均不能实现准确无误的符号定时。综合文献［6］可知，改进算法符号定时的性能优于文献［4－6］中提出的算法。在同步算法中，频偏估计的精确度取决于符号定时估计的准确性，而S＆C算法中的定时估计的平台效应使符号定时估计准确度下降。同样，经过改进的Minn算法及Park算法的定时估计也存在一定的问题，频偏估计必然会受到影响。本文提出的改进算法在保证符号准确定时的情况下完成频偏估计，将很大程度上提高频偏估计的性能。

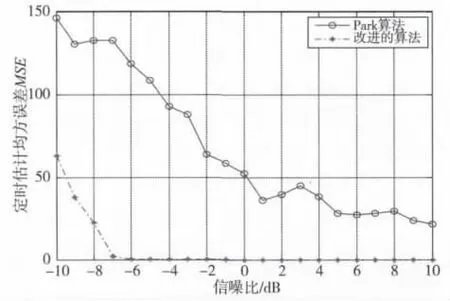
图6 电力线信道中两种算法的定时估计MSE

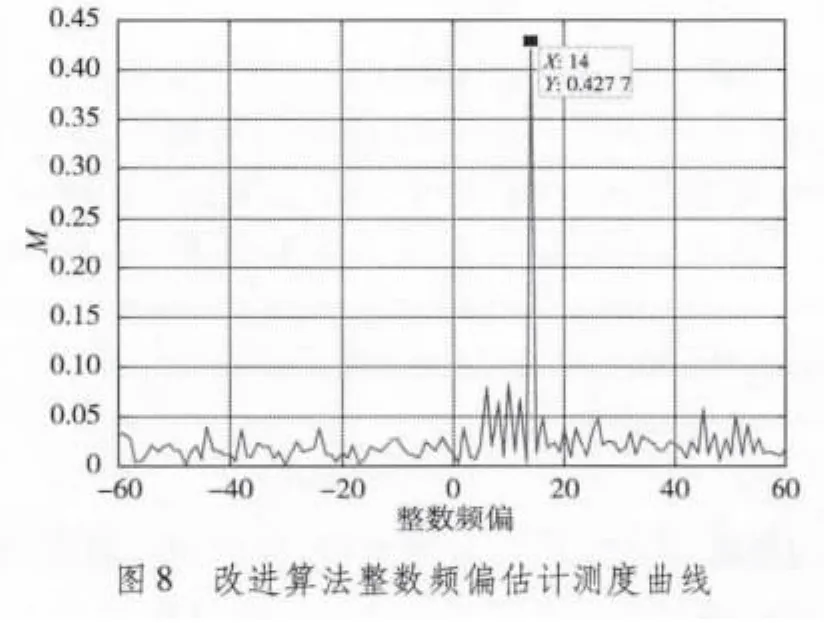
图7为不同信噪比时改进算法和S＆C算法的小数频偏估计性能比较。在AWGN信道下，OFDM系统要求频偏不大于子载波间隔的4%，在衰落信道中要求不大于子载波间隔的2%～3%。由图中可知，在信噪比较低的情况下，两者小数频偏估计MSE的值相差不大，且频偏都在要求的范围之内。但当信噪比逐渐增大，S＆C算法的曲线变化缓慢，而改进算法的均方误差值迅速减小。图8为信噪比为5 dB情况下的改进算法在时域进行整数频偏估计的测度曲线图，从图中可以看出即使在信噪比不高的情况下，整个测度曲线图只有一个峰值，且峰值明显，可看出峰值正好移动到14的位置。与S＆C算法不同的是，本算法的整数频偏估计是在时域完成的，省去了不必要的运算，而S＆C算法是在频域完成，有效地减小了计算复杂度。

5 总结

本文对OFDM在电力线通信环境中的同步问题进行了研究，仿真表明，本文提出算法的同步性能明显优于文献［4－6］提出的算法，该算法在提高符号定时精确度的同时，为下一步提高频偏估计性能打下了良好的基础，使频偏估计精度上升，且改进的算法频偏估计范围较大，而且改进的算法计算量减少。该算法仅利用一个训练序列同时实现符号定时和频偏估计，大大提高了数据传输的效率，同时满足电力线通信中准确、高效的传输要求，能较好地适应电力线通信的要求。

［1］赵海龙，张健，周劼，等.数据辅助的OFDM联合同步算法［J］.电视技术，2011，35(15):30－33.

［2］李琦，李宏伟，邓东虎，等.一种基于训练序列的改进OFDM联合同步方法［J］.电视技术，2012，36(19):146－150.

［3］SHI K，SERPEDIN E.Coarse frame and carrier synchronization of OFDM systems:a new metric and comparison［J］.IEEE Trans.Wireless Communications，2004，3(4):1271－1284.

［4］SCHMIDL T M，COX D C.Robust frequency and timing synchronization for OFDM［J］.IEEE Trans.Communications，1997，45(12):1613－1621.

［5］MINN H，ZENG M，BHARGAVA V K.On timing offset estimation for OFDM system［J］.IEEE Communications Letters，2000，4(7):242－244.

［6］PARK B，CHEN H.A novel timing estimation method for OFDM systems［J］.IEEE Communications Letters，2003，7(5):239－241.

［7］YAN Chunlin，LI Shaoqian，TANG Youxi.New frequency offset estimation method for OFDM systems by using CAZAC sequence［J］.Journal of Electrics ＆Information Technology，2006，28(1):139－142.