基于Retinex的低照度图像增强

程芳瑾，杜晓骏，马 丽，夏紫欣

(中国地质大学机械与电子信息学院，湖北 武汉 430074)

责任编辑:时 雯

图像因受退化因素影响，会导致质量严重下降，对比度、色彩、清晰度等出现明显失真。特别是因照度不足引起的图像退化问题始终是该领域研究的热点。

色彩恒常性是指在不同的外界环境中，人眼对物体色彩的感知在一定程度范围内总是保持恒定，色彩恒常理论模拟人类视觉系统的这一特殊功能实现对图像的处理，提高图像的可识别度，使图像具有更好的视觉效果。

第一个描述人类视觉系统的色彩恒常性的算法是由Land和McCann提出来的［1－2］。该彩色理论通过组合两个词retina(视网膜)和cortex(皮层)而称为Retinex理论。而后Land提出随机步行算法用来解决图像中照度不均匀的问题。由于随机步行算法复杂度较高，Jobson等人提出了经典的中心/环绕理论(SSR)［3］来降低复杂度。但SSR由于尺度不同会产生不同的问题，因此有学者提出多尺度Retinex(MSR)［4］用来解决不同尺度带来的问题。由于MSR色彩失真较大，后来提出了带色彩恢复的Retinex(MSRCR)，相对于MSR在色彩保持方面具有很大优势。在对环绕函数的选择上，Jobson在详细考察了各种不同环绕函数的性质和效果后发现:高斯形式的环绕函数综合效果最好。在尺度的选择上提出了自适应的参数选择。

本文将针对MSRCR算法在低照度图像处理中存在的颜色恢复失真问题，研究色彩恢复函数对处理后图像的影响。通过改进色彩恢复函数，提高图像的信息熵以及清晰度。

1 Retinex数学模型

1.1 单尺度Retinex算法

SSR算法是在Land提出的中心/环绕Retinex的基础上发展起来的，由于该算法数学形式以及物理实现都相对简单，因此应用较广泛。其数学形式为

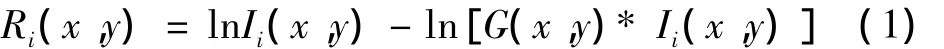
式中:Ii(x，y)为输入图像的第i个颜色通道;*表示卷积;Ri(x，y)表示Retinex的第i个通道的输出;G(x，y)为归一化中心/环绕函数。即

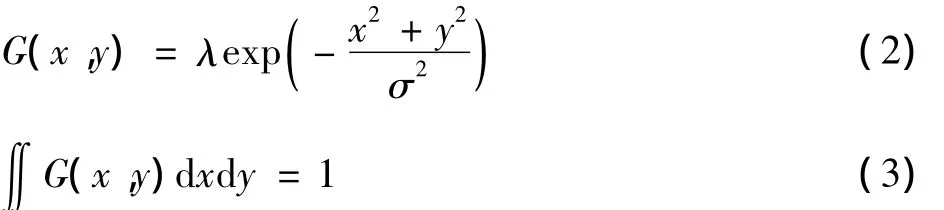
式中:σ为尺度参数，在离散情况下满足

1.2 多尺度Retinex算法

由于单尺度Retinex算法存在色彩保持和细节突出等方面的矛盾，因此提出了多尺度Retinex算法解决上述矛盾。许多文章提到了MSR与SSR以及直方图均衡等方法的效果对比［5－6］。多尺度Retinex是对单尺度Retinex的发展和延伸，它是几个单尺度Retinex的加权组合。其数学形式为

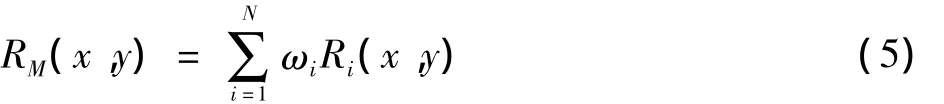
式中:Ri(x，y)为第i个尺度的SSR结果;ωi是第i个尺度的加权系数，并且满足ωi之和为1;N为尺度数，一般是3个尺度，分别是大尺度、中尺度、小尺度。根据文献［5］其经验值为:小尺度为图像的1% ～5%;中尺度为图像大小的10% ～15%;大尺度为图像大小的30% ～50%。

1.3 带色彩恢复的Retinex算法

SSR或者MSR算法处理RGB图像时，分别处理R，G，B这3个分量图，由于R，G，B各个分量图单独处理，在这个过程中3个通道有各自对应的补偿和增益，因此它们之间的比例关系会发生改变，造成颜色失真。将带色彩恢复的多尺度Retinex算法方法引入原始图像中3个色彩通道之间的颜色比例，对MSR结果进行处理，通过乘性色彩恢复函数的作用克服图像颜色的不饱和或失真，从而使得图像具有更好的颜色呈现。

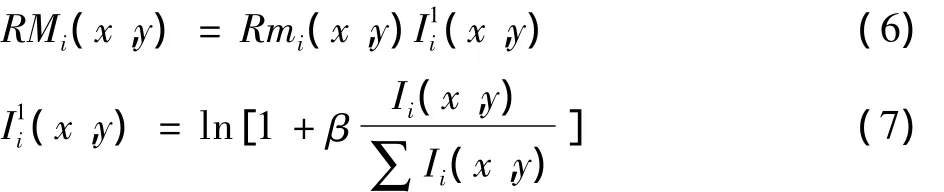
1.4 自适应补偿/增益

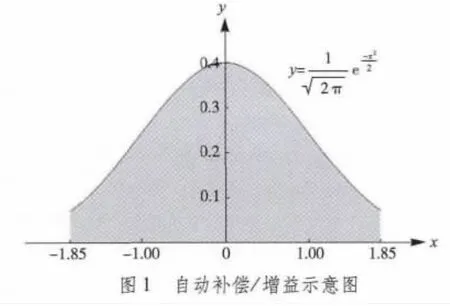
无论以上哪种Retinex算法都在对数域中进行，经常会出现负值，这时候需要通过补偿/增益［7］将像素值转换到显示器的显示范围内。补偿/增益的重点是找到起点和增益的倍数。假设处理后的图像所有像素值分布服从高斯分布，经过模拟仿真在均值上下1.85倍标准差左右截取，并将在这一区间的像素值线性地映射到0～255是一个效果较好的选择，如图1所示。这时处理后的图像信息熵较大，从而实现了处理后图像的自适应补偿增益。

2 余弦色彩恢复函数

Rahman等人认为Retinex不是作为人类视觉颜色常性的模型，而是作为数字图像增强的一个平台，从而不仅对比度得到了改进，颜色常性、亮度或色彩再现也得到了改善［7］。

在MSRCR中采用了色彩恢复因子，使得处理后的图像颜色更加接近原始图像的颜色。根据Rahman等人的论述，可以设计不同类型的色彩恢复方案用来恢复处理后图像的颜色。

在式(6)、式(7)中，通过MSR处理结果乘以恢复因子，以达到处理后图像颜色与原始图像颜色相接近的效果，从而以使颜色接近。通过式(6)和式(7)得到的图像有些像素颜色与原始图像出入较大。这是因为式(6)中每个像素均与色彩恢复因子相乘，而且β为一个常数，对于与原来颜色差别不大的像素也乘以一个比例因子，所以颜色会发生较大的失真，所以β应该为一个随色彩失真程度而变化的数值［8］。

传统做法是单独处理每个颜色通道，割裂了颜色本身，同时也受到光照的影响。将图像中每个像素的颜色看作三维矢量空间中的1个矢量，其中R，G，B分别是这个矢量的3个分量，这样把颜色当作1个矢量处理，而不是分开处理。再去掉光照影响，3个分量的比值就代表该颜色，可以考虑用色彩矢量之间的夹角余弦值来描述不同颜色之间的区别［9］，这个夹角范围是［0，π/2］。若夹角为0，余弦值为1，此时认为两个颜色相同;若夹角为π/2，余弦值为0，则两个颜色差异最大。本文设计的方案即根据夹角余弦值对MSR结果进行调整，使之与原始图像的颜色更加接近。当处理后图像像素矢量与原始图像像素矢量夹角较小时，说明颜色改变不大，因此只进行小幅度调整;当夹角较大时，说明处理后颜色失真很大，根据实际实验观察，这往往体现在亮度上，因而要大幅度调整其亮度以及颜色。

2.1 算法步骤

本文所提算法步骤如下:

1)假设原始图像为I，根据原始算法计算出单尺度处理结果I1;

2)计算I1与I对应像素的夹角余弦值矩阵cosθ(i，j);

3)计算i通道的色彩恢复函数

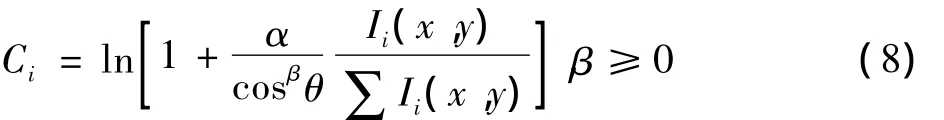
5)将几个尺度处理图像加权相加得

2.2 算法分析

若令算法里的β=0，则色彩恢复函数可以化简为

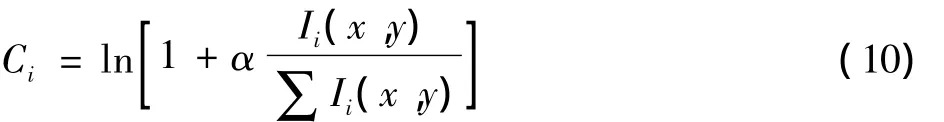
这就变成了经典的色彩恢复函数，因此本文色彩恢复函数是原始恢复函数的一个推广。它在处理低照度图像的时候具有更加优良的性质。

3 实验分析

图2采用了4幅具有一定代表性的低照度图像进行比较和分析，根据文献［7］从均值、标准差、信息熵、清晰度4个角度对原始色彩恢复函数(图3)与本文的余弦色彩恢复函数(图4)进行了对比和分析。

图2 原始图像

通过表1可以看出:本文的色彩恢复函数在标准差、信息熵和清晰度不同程度上优于原始算法，即图像的层次比原算法更加鲜明，图片中纹理较复杂，所含信息量较高，清晰度也高于原始算法。

表1 余弦恢复函数与原始恢复函数效果对比

4 小结

本文在对基于Retinex理论的图像增强算法研究的基础上，给出了余弦色彩恢复函数。在余弦恢复函数中使用了颜色的矢量夹角，较好地解决了因光照不均匀产生的颜色失真问题，使得图像颜色与原始图像更加接近，提高了图像的清晰度。对比仿真实验显示:相对于原始带色彩恢复的Retinex算法，本文的色彩恢复函数具有更好的色彩恢复能力和效果。同时原本不清晰的图像层次感、纹理细节、清晰度也得到改善。

［1］LAND E，MCCANN J.Lightness and retinex theory［J］.Journal of Optical Society of America，1971，61(1):7－21.

［2］LAND E.An alternative technique for the computation of the designator in the retinex theory of color vision［J］.Proceedings of the National Academy of Sciences of the United States of America，1986，83(10):3078－3080.

［3］JOBSON D J，RAHMAN Z U，WOODELL G A.Properties ans performance of a center/surround Retinex［J］.IEEE Trans.Image Processing，1997，6(3):451－462.

［4］RAHMAN Z U，JOBSON D J，WOODELL G A.A multiscale retinex for color redition and dynamic range compression［EB/OL］.［2012－12－02］.http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.55.6939.

［5］朱静.色彩恒常性理论及其在图像增强中应用研究［D］.北京:中国矿业大学，2011.

［6］刘高平，赵萌.基于亮度的自适应单尺度Retinex图像增强算法［J］.光电工程，2011，38(2):71－77.

［7］赵晓霞.基于Retinex理论的视频图像增强系统研究［D］.北京:中国矿业大学，2011.

［8］李建彬，韩军，邱君华.基于Retinex的旧视频序列增强算法［J］.电视技术，2011，35(5):21－24.

［9］袁兴生，王正志.亮度补偿变换矩阵的颜色恒常性算法［J］.中国图象图形学报，2012，17(9):1055－1060.