基于压缩传感的自同步图像水印算法

崔得龙，弓云峰，左敬龙

(广东石油化工学院a.计算机与电子信息学院;b.广东省石化装备故障诊断重点实验室，广东 茂名 525000)

责任编辑:时 雯

近年来，随着一种新的数据采集技术——压缩传感理论［1－2］的提出和发展，其在模拟信息转换、压缩成像、生物传感等领域已取得了一系列重要的研究成果。压缩传感理论利用信号的稀疏性先验知识，通过构造合适的测量矩阵，对信号进行线性随机投影，得到极少量的压缩测量值。由于测量值保留了信号的原始结构，因此可通过适合的优化算法精确重建原始信号。

在数字图像水印领域，压缩传感理论也得到了初步的应用［3－7］。文献［4］提出了一种基于压缩传感和LPDC码的图像水印算法。算法通过对原始图像进行线性随机投影，得到的压缩测量值经过LDPC编码，以水印方式嵌入到原始图像中;水印检测时，对篡改图像同样进行线性随机投影，得到的测量值作为边信息并进行LDPC译码。通过比较原始图像和篡改图像之间的压缩测量值实现篡改检测，实验结果表明该算法具有较强的抗攻击能力和较好的篡改检测能力。之后，周燕又提出一种基于哈希消息认证码的压缩传感水印算法［5］。文献［6］提出一种基于分块压缩感知的图像半脆弱零水印算法。算法先将图像划分成若干分块，分块大小可以根据水印数据量和篡改定位精度调整。再按照压缩感知理论对各个图像块进行观测，并将观测值作为零水印信息注册保存。实验结果表明，该算法可以准确定位非法篡改并借助水印信息恢复被篡改的区域。文献［7］提出一种基于压缩传感的视频篡改检测水印算法。算法采用压缩传感生成I帧图像的半脆弱认证水印并嵌入到I帧图像的中高频系数中，采用哈希运算生成P帧序号的完整性水印并嵌入到P帧的运动矢量中，实验结果表明该算法对视频帧间篡改和帧内篡改均具有很好的检测能力，能够精确到图像帧的子块。

针对目前基于压缩传感水印算法存在的抗几何攻击性能不足的现状，提出了一种基于压缩传感的自同步图像水印算法。算法将水印信息和同步信号嵌入原始图像稀疏化后的观测域中，使水印具有自同步能力。同时利用观测值局部特性，有效提高了在观测域中搜索同步信号的效率，较好地解决了同步信号鲁棒性和搜索量之间的矛盾。

1 压缩传感

压缩传感(Compressive Sensing，CS)的核心思想是对一类具有稀疏先验的信号，经过非线性采样得到小部分观测值，只要观测值包含足够的良好逼近信号，则原始信号可通过一定类型的线性或非线性解码机制高概率精确重建。CS理论由信号的稀疏变换、稀疏信号的非相干测量以及稀疏信号的重建3个要素构成。其中快速稳定的重建算法是CS的主要研究内容，也是CS走向实用化的关键。

设x∈Rn为原始信号，通过y=Φx得到随机投影信号y∈Rm，其中Φ∈Rm×n称为测量矩阵，满足限制等容条件［8］(Restricted Isometry Property，RIP)。若原始信号x是k－稀疏(有k≪n个非零元素)，则压缩传感的目标是通过随机投影的测量值y精确重建原始稀疏信号x。这一目标可等价为如下的优化问题

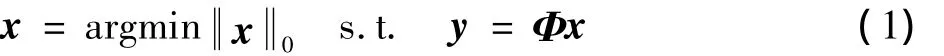
即信号x是式(1)最小化问题的解。

通常，基于线性规划的解码器求解需要cK个投影，其中 c≈ lb(1+N/K)［9］，重建复杂度为 O(N3)［10］。Cand和Tao［11］证明得到了限制等容条件下的稀疏恢复定理:若测量矩阵Φ具有参数(2n，0.2)的等容限制条件，则每一个n－稀疏向量x能够作为凸优化问题的唯一解从其测量Φx中被精确重建。

2 水印算法

2.1 同步信号

本文采用m序列作为同步信号。设{an}和{bn}是具有相同周期T的两个m序列，an，bn∈{－1，1}，则序列{an}和{bn}之间的互相关函数定义为

m序列{an}的自相关函数具有如下性质

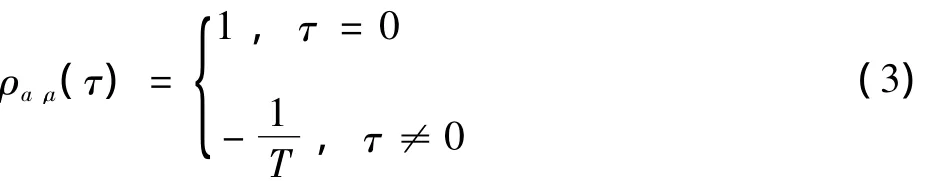
若τ=0时，m序列{an}和{bn}的互相关系数为

式中:h为阈值，取奇数。阈值h的含义为:如果序列{bn}最多只有(T－h)/2个比特与{an}不相同，则认为{bn}是一个同步信号。

2.2 水印嵌入

将水印序列和同步m序列都转换为{－1，1}序列，并按照图1方式构造序列{mi|mi∈{－1，1}}，其中同步m序列放在{mi}的前部，水印序列放在{mi}的后部［12］。

图1 隐藏数据结构

本文算法水印嵌入流程图如图2所示。

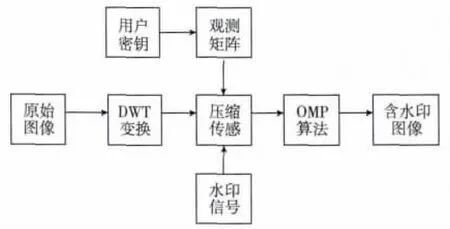
图2 水印嵌入流程图

详细的水印嵌入过程如下:

1)将原始图像I进行小波分解，得到稀疏小波分解系数矩阵A1。

2)对稀疏后的小波分解系数A1乘以用户密钥生成的观测矩阵，得到观测域压缩信号A2。

3)将观测域压缩信号A2一维化，根据式(5)进行水印嵌入［13］

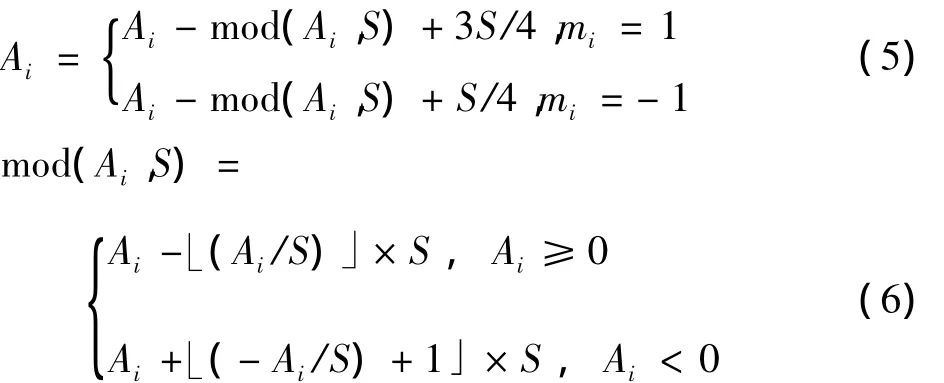
4)将得到的含水印序列重构为二维矩阵，采用OMP算法恢复得到含水印信息的稀疏信号A3。

5)对A3进行小波逆变换，得到含水印图像Iw。

2.3 水印提取

本文算法在进行水印提取时不需要原始图像，是一种盲水印算法，详细水印提取过程如下:

1)将含水印图像Iw进行小波分解，得到小波分解系数稀疏矩阵B1;

2)对稀疏后的小波分解系数B1乘以观测矩阵，得到观测域压缩信号B2;

3)将观测域压缩信号B2一维化，根据式(7)进行水印提取［12］

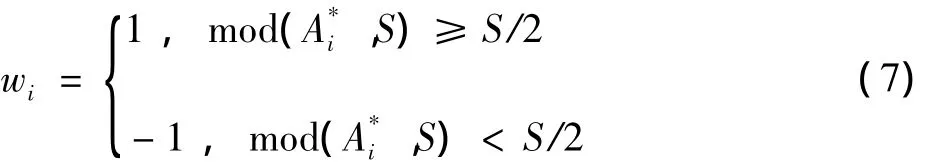
4)从提取的序列{wi}中确定同步信号后，然后进行水印信号的提取。

从式(7)可得，在Ai发生改变d时，即A*i=Ai±d，只要d∈(nS－S/4，nS+S/4)区间，都能够从A*i正确地提取到mi。

3 实验仿真

实验中使用Windows XP操作系统和MATLAB7.0作为实验仿真平台，选用Lena，Baboon，Peppers，Barbara 作为测试图像，同步序列为周期为63的m序列，水印序列为长度为1 024的随机序列，详细实验结果及分析如下。

3.1 透明性测试

本文算法使用PSNR衡量算法的透明性，定义为

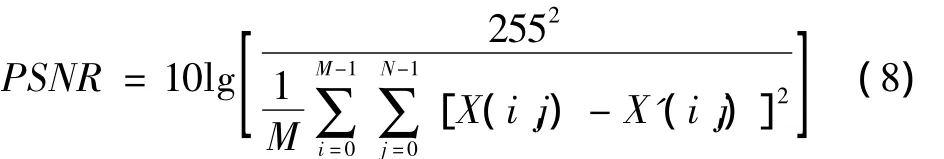
式中:X为原始图像;X′为嵌入水印后的图像。

图3a～图3d为原始标准测试图像，图3e～图3h为本文算法下的含水印图像。从图3的实验结果可见，本文算法含水印图像的平均PSNR为33.21 dB，满足不可见性要求。

3.2 稳健性测试

表1给出了本文算法在常见图像处理攻击下的鲁棒性，为了比较本文算法的性能，表1同时列出了文献［14］在相同实验条件下的实验结果。从表可见，本文算法和文献［14］算法对常见图像处理攻击下均具有较强的鲁棒性，同时本文算法在高斯噪声、JPEG压缩、高斯滤波等攻击下的性能优于对比文献［14］。

图3 算法透明性测试

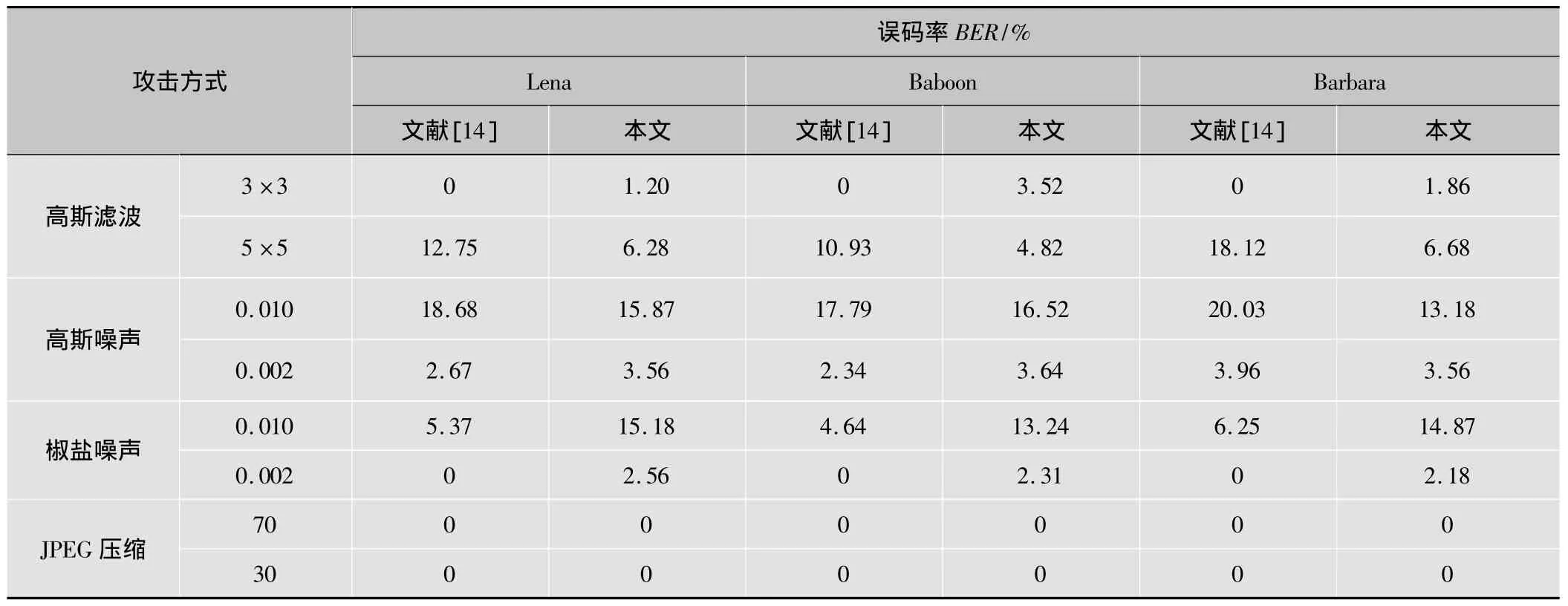
表1 数字水印对常规信号处理的抵抗能力

表2列出了本文算法抵抗几何攻击的能力，为了便于比较，表2同时列出了文献［14］在相同实验条件下的实验结果。从表2可见，无论是单一几何攻击还是联合几何攻击，本文算法的性能均优于对比文献算法。由于本文算法在进行水印嵌入时使用了同步码m序列，有效提高了算法抵抗各种几何攻击的性能。

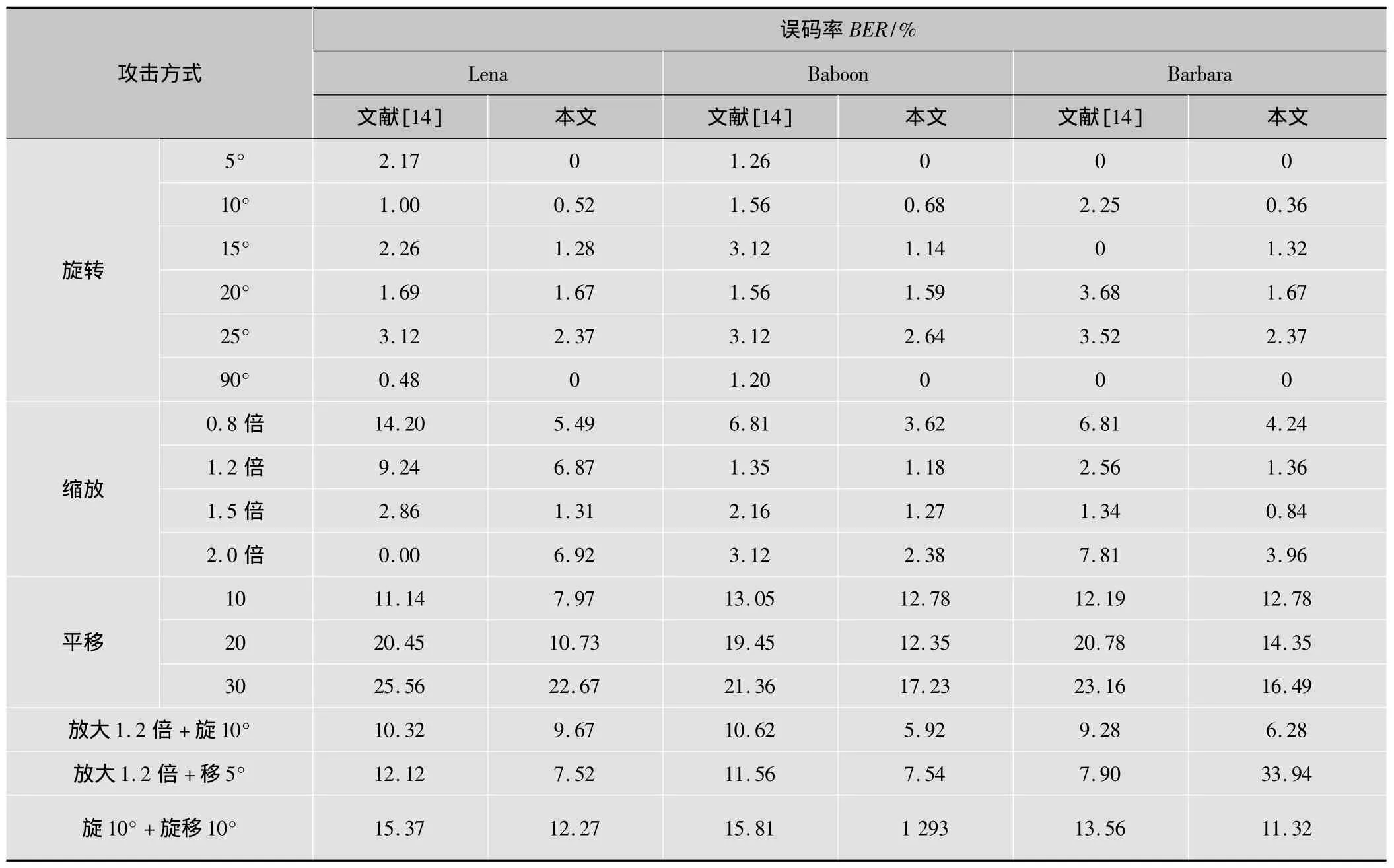
表2 数字水印对几何攻击及联合攻击的抵抗能力

3.3 提取测试

本文算法的安全性取决于用户密钥生成的观测矩阵，不同的用户密钥产生不同的高斯随机矩阵，因而提取的水印序列也不相同。为验证算法的安全性，随机生成1 000组用户检测密钥进行水印提取，并设置第500组为原始用户密钥，用户密钥与提取水印之间的相关系数NC关系如图4所示。

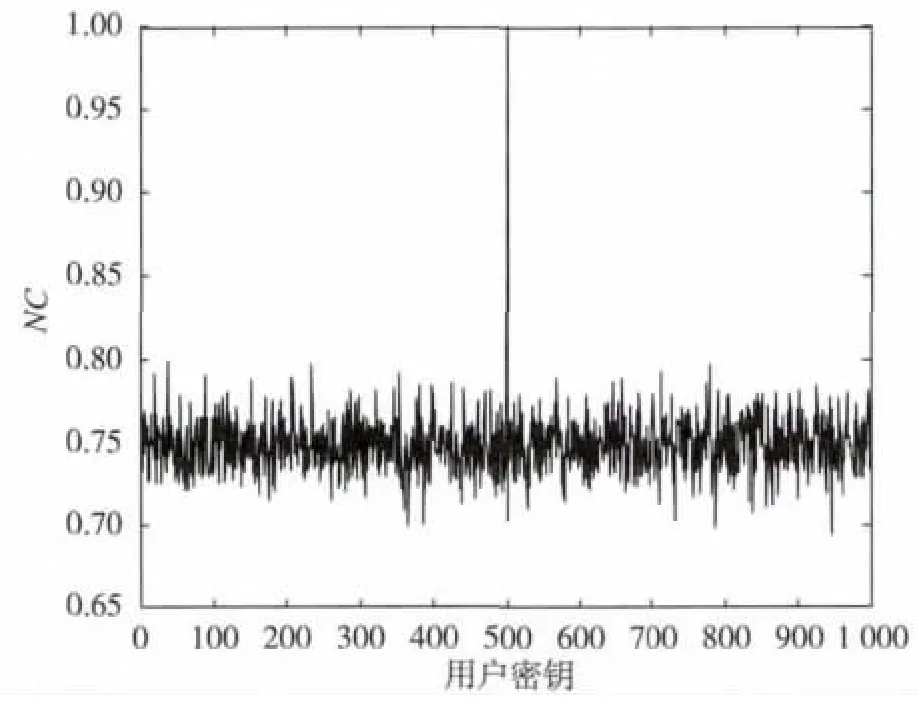
图4 安全性分析测试结果

相关系数NC的定义为

式中，x(i)和x′(i)分别为原始水印序列与提取的水印序列。从图4可见本文算法对用户密钥敏感，是一种安全的数字水印算法。

4 结论

针对目前基于压缩传感水印算法存在的抗几何攻击性能不足的现状，提出了一种基于压缩传感的自同步图像水印算法。算法主要特点是:1)将水印信息和同步信号嵌入原始图像稀疏化后的观测域中，使水印具有自同步能力;2)利用观测值局部特性，有效提高了在观测域中搜索同步信号的效率，较好地解决了同步信号鲁棒性和搜索量之间的矛盾。此外，本算法在提取水印时无须原始图像，是一种盲水印算法，因此本文算法具有较强的实用性，具有一定的应用价值。今后的研究将深入分析压缩传感观测域变换系数的统计特性，设置更合适的嵌入算法，进一步降低算法的鲁棒性和抗几何攻击性能。

［1］DONOHO D L.Compressed sensing［J］.IEEE Trans.Information Theory，2006，52(4):1289－1306.

［2］童露霞，王嘉.基于压缩传感的重构算法研究［J］.电视技术，2012，36(11):38－40.

［3］VALENZISE G，TAGLIASACCHI M，TUBARO S.A compressive sensing based watermarking scheme for sparse image tampering identification［C］//Proc.ICIP 2009.［S.l.］:IEEE Press，2009:1265－1268.

［4］周燕，周灵.基于压缩传感和LPDC码的图像水印算法研究［J］.小型微型计算机系统，2011，32(3):572－576.

［5］周燕，张德丰，马子龙.基于压缩传感的图像哈希水印算法研究［J］.中山大学学报:自然科学版，2010，49(6):58－63.

［6］赵春晖，刘巍.基于分块压缩感知的图像半脆弱零水印算法［J］.自动化学报，2012，38(4):609－617.

［7］曾凡智，卢炎生，周燕.基于压缩传感的半脆弱水印的视频篡改检测算法［J］.电路与系统学报，2011，16(4):87－93.

［8］BLUMENSATH T，DAVIES M.Iterative hard thresholding for compressed sensing［J］.Applied and Computational Harmonic Analysis，2009，27(3):265－274.

［9］方红，章权兵，韦穗.基于亚高斯随机投影的图像重建方法［J］.计算机研究与发展，2008，45(8):1402－1407.

［10］CANDES E，TAO T.Error correction via linear programming［C］//Proc.FOCS 2005.［S.l.］:IEEE Press，2005:295－308.

［11］CANDES E，TAO T.Decoding by linear programming［J］.IEEE Trans.Inform.Theory，2005，51(12):4203－4215.

［12］吴绍权，黄继武，黄达人.基于小波变换的自同步音频水印算法［J］.计算机学报，2004，27(3):365－370.

［13］刘九芬.小波理论及其在图像压缩和数字水印中的应用［D］.杭州:浙江大学，2001.

［14］王向阳，朱丹丹.基于非下采样Contourlet变换的伪Zernike矩水印算法研究［J］.计算机应用与软件，2011，28(5):278－280.