基于点集拓扑群分形变幻的云计算加密方法

郎登何

(重庆电子工程职业学院，重庆 401331)

责任编辑:魏雨博

云计算建立在资源虚拟化数据中心的基础之上，通过协商与用户建立服务层协议，以服务的形式向用户提供按需的、可扩展的、满足QoS要求的计算资源，而用户只需付费即可。在这样的一种环境中，用户不再需要自备一台功能完善的个人PC来处理自己的数据和运算，而是通过使用简单的、功能有限的上网设备，例如手机、PAD等与云建立联系，可以把数据信息存入云中，或从云中获取强大的计算能力或是使用最新版本的服务，从而可以随时随地进行相应的工作。而企业也不需要再维护自己的数据中心，而是可以租用云中的可扩展存贮及计算资源，从而可以更专心于自己的业务。

云计算具有如此强大的优势，但因为云计算特有的数据和应用外包、虚拟化、多租户跨域共享等特点，带来了前所未有的安全挑战。

云计算加密系统已经成为云计算安全的重点研究领域［1－2］，而加密系统中密钥和算法又是加密系统最为关注的部分，本文运用点集拓扑群分形变幻的方法实现密钥生成，这比不同密钥的随机生成更具有发散性与随机性，因此采用该方法生成的密钥进行加密更在很大程度上能加强云计算数据交互的安全性。如人脸、语音、指纹等生物特征点，在相关可控和不可控点集拓扑变换方法驱动下都可以成为相应的可信加密/解密算法和密钥。

1 云计算安全体系结构

云计算是定制与交付服务的超级计算，其最大的优点是虚拟服务平台高效且定制服务总类丰富，具有广阔的市场应用前景，但是安全性问题一直是云计算的一大难点［3］。云计算的不安全性表现在多个方面，比如信息体的伪造、变造、假冒、抵赖、木马攻击、病毒损毁等，这些使得云计算的应用推广受到阻碍。

其实不信任、不安全对云计算的危害不仅发生在服务定制和交付这两个出入口，也发生在中间过程，即服务的组织、加工、整理、包装等过程，因此在整个云空间，云可信、云安全对正常的网络社会经济秩序构成了巨大的挑战［3］。图1描述了云计算安全防护体系结构。

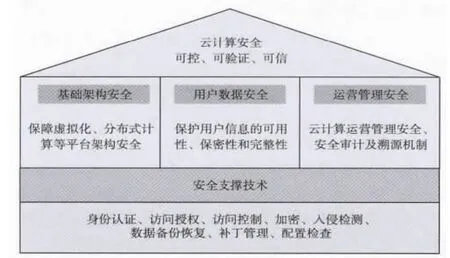
图1 云计算安全防护体系结构图

要实现可控、可信、可验证的云计算安全系统必须保证基础架构安全，用户数据安全级运营管理安全。作为云计算的使用者来说，用户数据安全是最为关注的问题，保护用户信息的可用性、保密性和完整性是云计算必须攻克的难题，而身份验证、访问授权、访问控制及加密则是用户数据安全需要解决的具体问题。

本文从云计算加密系统方面展开研究，密钥生成是加密系统最关键的部分，其次是加密算法，采用点集拓扑分形变幻的密钥生成随机性强、安全性高，而且分形变幻效率高，适合作为密钥生成运算方法。同时采用人脸、语音、指纹等生物特征点作为分形变幻的数据源［4］，具有唯一性，进一步提高了加密系统的安全性，能给不同用户数据打上用户特有标签，有助于保护用户数据隐私。

2 点集拓扑群分形变幻的云计算加密实现

2.1 点集拓扑分形变幻密钥生成

2.1.1 随机码生成

在密码学中，随机序列的作用不言而喻，它的生成一般使用伪随机生成器，包括给定长度为K的一个随机二进制序列(称为种子SEED)作为算法的输入，算法输出一个看上去似乎随机的二进制序列［5］。

随机数是指用数学递推公式所产生的随机数。不同的开发环境提供的生成随机数的函数和方法不同。在典型情况下，它会输出一个均匀分布在0和1区间内的伪随机变量的值。随机数发生器是在计算机中产生随机数的方法，经常采用如下公式

式中:b，c，d为正整数，d称为由式(1)所产生的随机序列的种子，an是随机数序列。

由式(1)可以看出，所产生的随机序列的值与b，c，d有一定的关系。这种只在一定程度上满足随机性的序列称为伪随机数。用这个公式产生0～65 536的a1，a2，…，an随机数序列，故称为232步长的倍增谐和随机数发生器［6］。

2.1.2 点集拓扑群对象的模型

如图2所示，点集“拓扑群论”对象可以表示为由矩形框包围点集的对象BioTPM［N］。

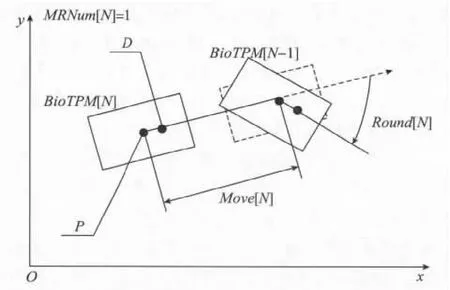
图2 点集拓扑群对象运算模型

点集拓扑群论运算模型说明如下:

1)设定基准点和基准方向点

设定该对象模型的基准点和基准方向点步骤，图2中的P、D所示，子集也如此。

2)设定坐标系

设定该对象模型的坐标系，如图2中xOy坐标系所示，子集也如此。

3)设定环运算特征

点集“拓扑群论”对象运算特征表示为，首先进行加法交换群位移操作，再进行乘法对称群旋转操作，也可在该乘法对称群旋转操作的同时增加乘法对称群翻转操作。当然规则要事先确定，子集也如此。在图2中，位移方向由P、D连线的箭头指示，位移量由P、D箭头连线长度Move［N］指示，Move［N］是BioTPM［N］到BioTPM［N+1］的基准点P位移值;旋转由 Round［N］弧线箭头指示，旋转量由Round［N］弧长指示，Round［N］是BioTPM［N+1］的旋转值。

需要说明的是，先设定加法位移后，再乘法旋转，该两项操作为一次组合操作，在“群论”中称为环运算。该环运算次数为MRNumber［N］。图2只进行了一次加法位移和乘法旋转，因此MRNumber［N］值为1，该环的运算次数不改变点集“拓扑群论”对象的属性。

上述基于点集“拓扑群论”对象的定义中，涉及该环运算特征参数的确定，即加法位移量Move［N］、乘法旋转量 Round［N］、环运算次数 MRNumber［N］。同时，该点集“拓扑群论”对象的非线性变换和变幻要求该环运算特征参数非线性。Move［N］、Round［N］、MRNumber［N］的初始化值来自于节点“子集自组织”，这些值的确定是点集拓扑群论运算的关键点。

2.1.3 点集拓扑群分形变幻环运算

特征图像点的集合用G［K］表示，G［K］中又有子集G1［K］，G2［K］，…，Gn［K］，设定 Gn［K］为最后一个子集。提取自组织于集合G［K］的两个子集G1［K］、Gn［K］，参与基于混沌的散列运算。设定位移量 Move［K］是子集G1［K］的散列运算值、乘法旋转量Round［K］是Gn［K］的散列运算值、环运算次数 MRNumber［K］是 G1［K］⊕Gn［K］或 G1［K］%Gn［K］的散列运算值。

基于群特征的运算是点集“拓扑群”分形变幻环运算，设定点集“拓扑群”分形变幻环运算由单位拓扑群分形变幻环运算构成，是该单位群的加法运算。设定单位群是连续的单位环运算。其中，单位环运算是单位点集拓扑群环运算的简称，是该点集先加法位移后，再乘法旋转的运算，而该分形变幻则是反复的“单位环”运算。具体运算流程如图3所示。

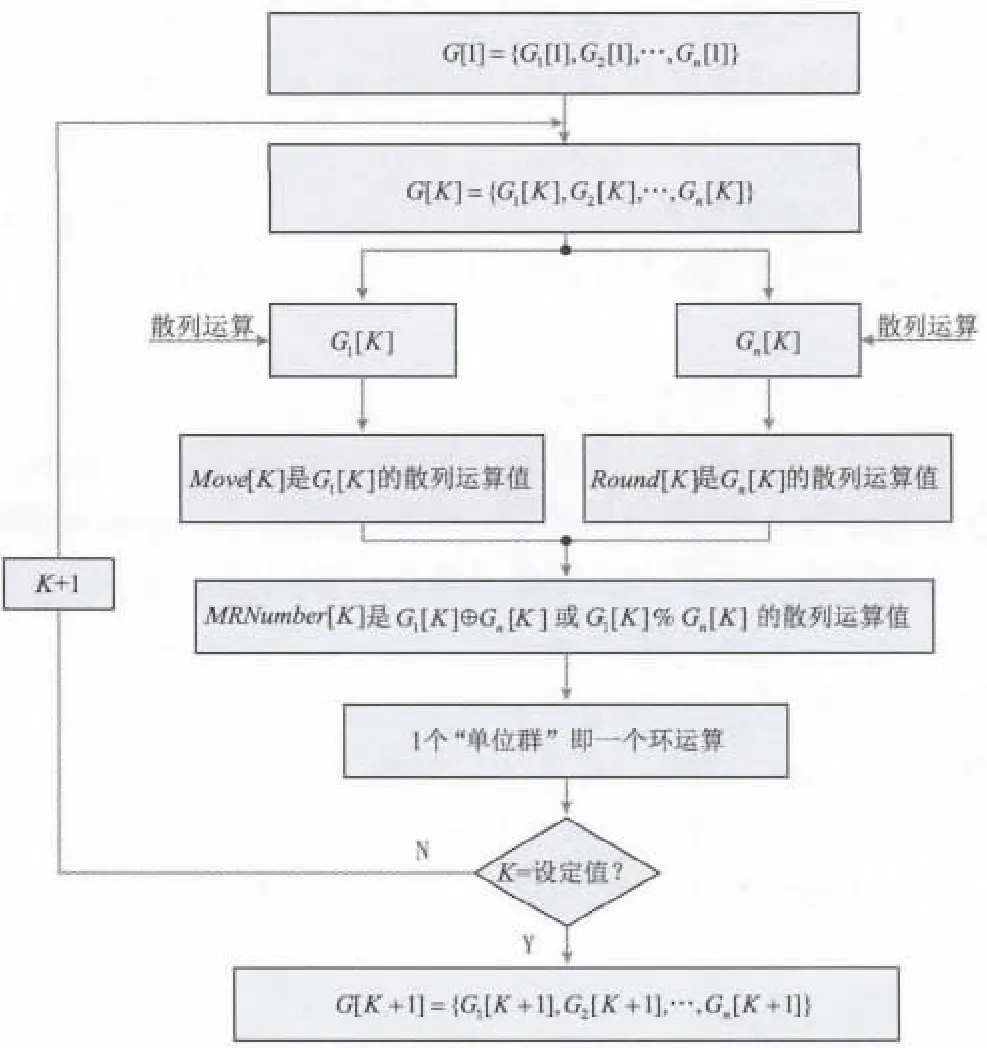
图3 点集拓扑群分形变幻环运算流程图

“单位群”加法运算的数学规定如下:

1)1个“单位群”+0个“单位群”=1个“单位群”，即进行该连续的“单位环”运算。

2)1个“单位群”+1个“单位群”=2个“单位群”，即进行2连续的“单位环”运算。

3)1个“单位群”+K个“单位群”=K+1个“单位群”，即K+1连续的“单位环”运算。

点集拓扑群分形变幻环运算的流程步骤如下:

1)输入集合G［K］及子集 G1［K］，G2［K］，…，Gn［K］，初始化1个“单位群”运算;

2)设定子集G1［K］为集合G［K］的自组织对象;

3)设定子集Gn［K］为集合G［K］的自组织对象;

4)设定Move［K］是G1［K］的散列运算值，Round［K］是 Gn［K］的散列运算值，MRNumber［K］是G1［K］⊕ Gn［K］或 G1［K］%Gn［K］的散列运算值;

5)设定K个“单位群”运算的循环，K的初始化值为1;

6)设定1个“单位群”即一个连续环运算及其运算规则，循环次数为MRNumber［N］次;

7)设定K个“单位群”运算的循环限制值;

8)输出K个“单位群”运算的点集“拓扑群”分形变幻环运算值。

2.1.4 密钥生成

运用VC++实现点集拓扑分形变幻运算如图4所示。

图4 点集拓扑分形变幻密钥生成程序运行图

打开选择特征数据，本文选择指纹图像作为特征数据，然后选择变幻次数，选择100次，然后选择保存路径及保存名字，最后选择应用，变幻结果立即生成，且存入保存路径的log.log文件中。

变幻结果如图5所示，显示由子集G1［K］和G［K］组成集合G［K］一系列数据，其中m和m′分别表示G1和G2作平移旋转操作的次数。从开始到结束显示每一系列数据都不同，呈现很大的变幻随机性。

Move［K］、Round［K］、MRNumber［K］数值范围从Move［1］=1、Round［1］=0、MRNumber［1］=3，直到100次单位点集“拓扑群”分形变幻环运算，呈现Move［100］=6、Round［100］=0、MRNumber［100］=3。文件列从子集G1［2］和G2［2］组成的集合G［2］系列数据开始，到子集 G1［101］和 G2［101］组成的集合 G［101］系列数据结束，是100组集合G［K］变幻数据，第1组集合是初始数据。

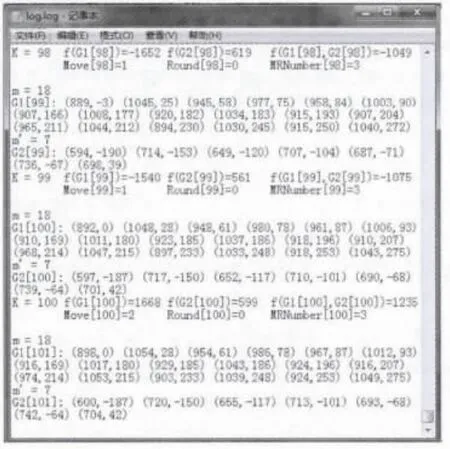
图5 密钥生成结果图(截图)

利用此分形变幻的随机序列作为密钥对数据进行加密，具有非常高的安全性，密钥的生成以指纹图像作为输入特征值，具有唯一性、可靠性及更高的辨识性。

2.2 加密实现

加密的过程就是根据密钥和明文生成密文的过程［7－8］，密钥由指纹图像经过点集拓扑分形变幻而得，密文由加密算法而得，具体过程如图6所示。

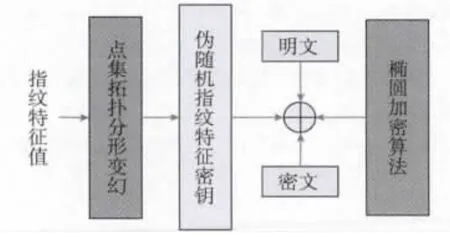
图6 加密过程图

2.2.1 椭圆加密算法

本文采用椭圆机密算法，它与传统的基于大质数因子分解困难性的加密方法不同，椭圆加密算法ECC(Elliptic Curve Cryptosystems)通过椭圆曲线方程式的性质产生密钥，ECC 164位的密钥产生一个安全级，相当于RSA 1 024位密钥提供的保密强度，而且计算量较小，处理速度更快，存储空间和传输带宽占用较少，因此常被用于安全级高的加密系统中［9］。

椭圆曲线即三次平滑代数平面曲线(Smooth Algebraic Plane Curve)，可在适当的坐标下，表达成Weierstrass方程式

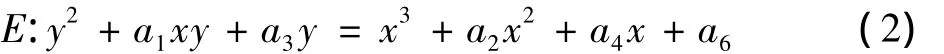
除了特殊系数，一般而言，可在适当的坐标下，表示为

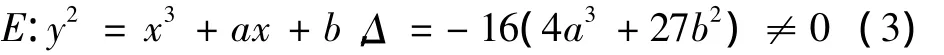
在系数K上的平面图形，其中E也包括无限远点O。

令E:y2=(x3+ax+b)mod p为一椭圆曲线，令P和Q为E(FP)上的两点，假设点Q由点P生成。在E上的离散对数问题就是要解Q=［k］P的K值。

令E为定义在FP上的椭圆曲线，则E(FP)的个数满足#E(Fp)=p+1+t，其中误差项 |t|＜2，则

给定私有密钥k，K=k·#E(Fp)，就可计算出经过加密后的公开密钥K，其中p的值越大，安全性越好，但加密速度变慢，一般而言，p取200 bit左右。

2.2.2 椭圆加密实现

首先通过点集拓扑变幻将指纹图像生成密钥，然后将密钥和要加密的明文，通过椭圆加密算法生成密文，密文通过相同的密钥进行解密，恢复原文，依据此功能，通过VC++开发程序，程序界面图如图7所示。

图7 椭圆加密程序运行图(截图)

如图7所示，对明文12981进行椭圆加密，加密的密钥来自于点集拓扑分形变幻运算，加密后的密文为(646034，519257840)(672986，519297773)，点击“解密”按钮，恢复为原文12981。采用此加密方法具有速度快、安全性高的优点。

3 结语

本文重点介绍了点集拓扑群分形变幻运算的指纹特征密钥生成过程，随机码生成一直是加密过程的重要组成部分，该方法将数学的点集拓扑与分形变幻运算两者结合，采用该方法生成密钥，随机性高，不易被破解，而且算法速率高，具有一定的创新性和研究价值，同时采用安全性好且速度快的椭圆加密算法，完成明文至密文的加密过程。

本文只对云计算安全的数据加密系统进行了研究，而对身份认证、入侵检测等保证用户数据安全没有做展开研究，这是后续云计算安全研究中应当着重关注的问题，同时也需要对基础架构安全和运营管理安全等方面进行资料收集与调研，加强云计算安全防护体系。

［1］王培海.基于Android的移动云存储系统设计与实现［J］.电视技术，2011，35(15):94－97.

［2］ARSHAD J，TOWNEND P.Cloud computing security:opportunities and pitfalls［J］.International Journal of Grid and High Performance Computing，2012，4(1):52－66.

［3］Overall cloud computing security risk assessment analysis［EB/OL］.［2012－12－01］http://wenku.baidu.com/view/3caee9f04693daef5ef 73d02.html.

［4］ZHU Huahong，HE Qianhua，TANG Hong，et al.Voiceprint－biometric template design and authentication based on cloud computing security［C］//Proc.2011 International Conference on Cloud and Service Computing.Hong Kong，China:［s.n.］，2011:302－308.

［5］黄汝维，桂小林，余思，等.云环境中支持隐私保护的可计算加密方法［J］.计算机学报，2011，34(12):2391－2402.

［6］朱和贵，张祥德，杨连平，等.基于人体指纹特征的随机序列发生器［J］.计算机研究与发展，2009，46(11):1862－1867.

［7］梁宇，路劲，刘笠熙，等.一种云计算环境下的加密模糊检索方案［J］.计算机科学，2011，38(10):99－105.

［8］徐剑，周福才，陈旭，等.云计算中基于认证数据结构的数据外包认证模型［J］.通信学报，2011，32(7):153－160.

［9］LI Jin，WANG Qian，WANG Cong，et al.Fuzzy keyword search over encrypted data in cloud computing［EB/OL］.［2012 －12 －05］http://www.docin.com/p－360587334.html.