基于PCA－SIFT特征的目标识别算法

王 鹤，谢 刚

(太原理工大学信息工程学院，山西 太原 030024)

责任编辑:时 雯

目前，图像识别技术备受国内外学者青睐，在计算机视觉、三维目标识别、地图与地形匹配等领域大显身手，相关算法应运而生。但传统算法局限性很强，当环境发生复杂变化时，这些算法就显得无能为力。David G.Lowe在前人工作的基础上，于2004年提出了完善的SIFT特征提取算法［1－2］。大量实践印证，面对物体旋转、背景遮挡、尺度缩放、外界噪声等复杂情形时，SIFT算法处理效果都很好，但在描述特征点时，使用的维数偏高，造成数据计算量非常大，且提取的特征点较多，造成特征匹配时间过长，降低了匹配效率。针对以上不足，本文采用PCA－SIFT算法对原始算法中的特征点描述符进行降维，提出了一种基于PCA－SIFT算法的目标匹配与识别方案，从而快速、准确地进行目标匹配与识别。

1 构建SIFT特征向量

SIFT算法以尺度空间为主体思想，首先构建DOG金字塔，在尺度空间内找到极值点，然后精确定义关键点的位置和主方向，保证算法的尺度与旋转不变性，最后形成多量、高速的128维的SIFT描述符。具体步骤如下。

1.1 DOG尺度空间的生成

将原始图像与高斯核卷积，获得原始图像的尺度空间描述，即

式中:σ是尺度坐标;(x，y)是空间坐标;G(x，y，σ)是高斯滤波函数，如

稳定特征点的提取是在DOG尺度空间中进行的，高斯差分尺度空间D(x，y，σ)的公式为

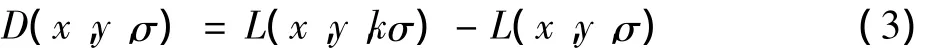
通过比较同一层和相邻上下两个尺度空间的26个点，将极大值和极小值作为候选关键点。

1.2 确定特征点位置

对Taylor展开式进行曲线拟合，得到修正后的位置、尺度信息，从而精确定位极值点。另外，受边缘响应和噪声的影响，DOG算子稳定性降低，通过设定阈值的方法，以及运用海森矩阵的性质，保留最优关键点，剔除不稳定点，从而减弱外界噪声干扰，增强DOG算子的稳健性。

1.3 特征点主方向的确定

采用梯度方向分布法保持算法的旋转不变性，点(x，y)处的梯度模值与主方向如式(4)、式(5)所示

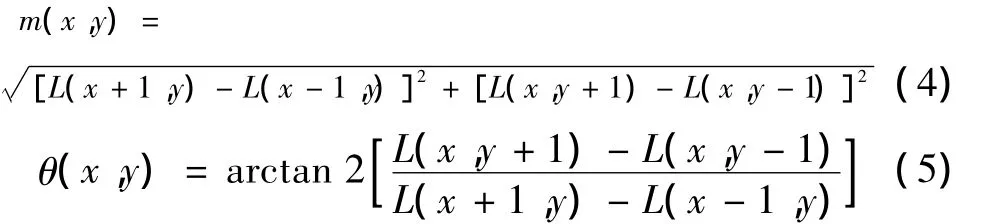
式中:L是关键点的尺度;m(x，y)是点(x，y)的梯度模值;θ(x，y)为点(x，y)的梯度方向，取值范围是(－180，180］。统计直方图像素点的梯度方向分布，可知峰值处为主方向。

1.4 特征相量描述子的建立

以关键点为圆心，画出16×16的圆形区域，然后把该圆域等分成4×4的子邻域，计算子区域梯度直方图，由于梯度方向是8维矢量，这样每个点便有128维的向量对其进行描述，这就是SIFT特征向量。

1.5 PCA－SIFT描述符的构造

主成分分析方法的目的在于使用低维子空间表示维数较高的数据。PCA－SIFT算法和原始SIFT算法具有相同的描述过程，即亚像素位置、尺度和主方向［3］。用PCA对128维SIFT特征向量降维过程如下:首先，将两幅待匹配图像中n个点的SIFT描述符x1，x2，…，xn作为样本，算出128维均值向量μ和128×128的协方差矩阵R;其次，计算协方差矩阵R的特征向量e和p个特征值，其中p=128，并将特征值从大到小进行排列，则有λ1≥λ2≥…≥λp及对应的特征向量{e1，e2，…，ep}，选出对应最大的n个特征值的特征向量作为主成分方向，根据实验效果，本文选取n=20;最终，构造出一个p×n的矩阵A，它的列由n个特征向量组成。将原始128维SIFT特征向量按照式(6)投影到这个n维子空间，得到特征向量的主成分表示为 y1，y2，…，yn，有

因实验选取n=20，所以矩阵A的大小为128×20，xk的大小为1×128，因而xk×A便得到大小为1×20的矩阵，即:每个yk就是一个20维的特征描述向量，这样就把原始的128维SIFT特征向量降成了20维的PCA－SIFT特征向量。

1.6 PCA－SIFT特征相量匹配

首先，算出PCA－SIFT特征向量的欧氏距离，找出欧氏距离的最小值，还有次最小值，求出二者的比值，如果比设定的门限值小，就认为匹配成功。其次，通过随机抽样一致性算法，利用特征集合的内在几何约束关系进一步去除误匹配点，从而提高匹配精度。

2 实验分析结果

实验是在 CPU为 Intel Corei3 2.20 GHz、内存为2 Gbyte的 PC 机上，采用软件MATLAB7.1 平台进行［6］，通过两组实验证明算法的可行性。

2.1 实验1:PCA－SIFT算法性能的验证

选取50幅图像，大小约为550×450，分别针对不同的情况进行实验，由于篇幅有限，本文列举出部分效果图及运算对比结果，如图1～3和表1所示。

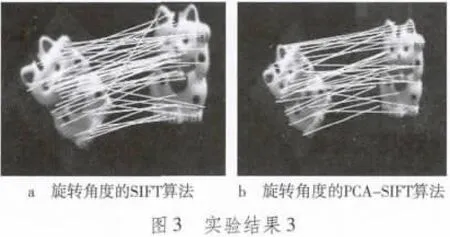
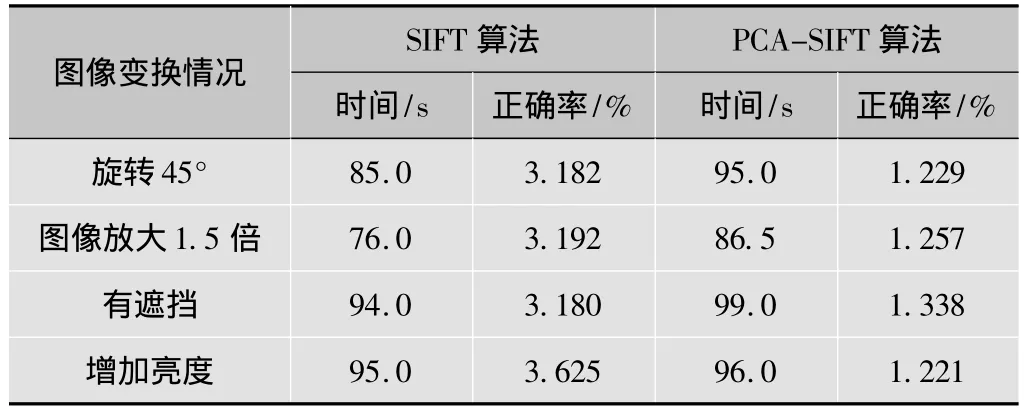
表1 两种算法匹配结果比较

根据实验1可得出下述结论:1)从匹配的正确率来看，无论图像在旋转、光照改变、缩放，还是有物体遮挡的情况下，PCA－SIFT算法的匹配性能都比SIFT算法稳定。2)从匹配时间来看，基于PCA－SIFT的匹配算法大大降低了匹配的时间，提高了图像的匹配效率。基于上述PCASIFT算法的优点，非常有利于将该算法运用到实时处理的目标识别系统中。

2.2 实验2:目标识别实验

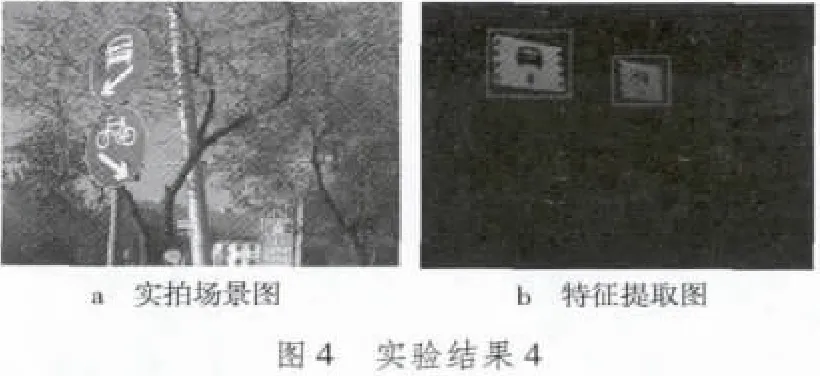
将实验1中的PCA－SIFT匹配算法应用于交通标志的匹配与识别中［4］。实地拍摄的交通标志图片如图4a所示，根据形状以及颜色特征对拍摄的图像进行粗匹配，以便找到含有交通标志的区域。图4b为粗匹配后，利用文献［5］中的方法提取感兴趣的特征区域。

经粗匹配找出含交通标志的区域后，采用PCA－SIFT算法提取特征向量，并与其所对应的交通标志子数据库中的图像的特征向量进行匹配筛选，得出以下结果，如图5所示。

图5 实验结果5

为方便司机识别，将最终的图像输出窗口设置为图6所示，窗口的右侧是已备好的交通标志子数据库模型，经过计算机处理识别后，系统自动识别出的交通标志对应模板图形便会显示在场景图周围。

3 结语

本文采用PCA－SIFT算法对数字图像进行降维处理，大大减少了特征向量的计算时间，与此同时，本文提出的匹配方案有效地减少了匹配的特征点数目，缩短了目标识别的时间。实验表明，该算法不但具有较高的识别精度，而且实时性能良好。

［1］LOWE D G.Distinctive image feature from scale－invariant interest points.International［J］.Journal of Computer Vision，2004，60(2):91－110.

［2］LOWE D G.Distinctive image features from scale－invariant keypoints［J］.International Journal of Computer Vision，2004，60(2):91－110.

［3］KE Y.PCA－SIFT:A more distinctive representation for local image descriptors［C］//Proc.CVPR 2004.［S.l.］:IEEE Press，2004:506－513.

［4］许少秋.户外交通标志检测和形状识别［J］.中国图象图形学报，2009，14(4):707－711.

［5］张剑飞，陈树越.基于支持向量机的交通视频人车识别研究［J］.电视技术，2011，35(15):1－3.

［6］高成，董长虹.MATLAB图像处理与应用［M］.北京:国防工业出版社，2007.