CDMA下行同步算法设计与FPGA实现

罗 森，田增山，周启平

(重庆邮电大学无线定位与空间测试重点实验室，重庆 400065)

在CDMA(Code Division Multiple Access)扩频通信系统中，同步技术作为码分多址的三大支撑技术之一，起着至关重要的作用。在CDMA系统下行同步过程中，利用PN短码良好的相关性，将前向数据与不同相位的PN短码序列进行相关，找到最高相关峰值对应的相位，从而完成短码同步。以往CDMA的同步、解扰和解Walsh等相关算法［1］主要是基于DSP实现，但通常需要多块DSP来共同完成，且CDMA中长码生成和实时性处理对DSP来说是相当大的挑战。但随着FPGA技术的快速发展和数字信号处理IP核的成熟，如FFT，FIR，DDS和ALTMULT_COMPLEX等IP核，基于FPGA的信号处理得到广泛的应用。基于FPGA的CDMA同步算法实现，主要以滑动相关法为主，该方法虽然实现简单，但实时性较差。本文针对CDMA下行同步快速高效的要求，完成了CDMA下行同步的算法设计，并以FPGA的思想构建同步模块，利用Altera的Stratix II系列芯片作为硬件平台进行板级调速，该方法最终应用到实际项目中。

1 CDMA下行同步算法

1.1 PN序列的自相关特性

CDMA导频信道中传输的数据，是周期为32768个码片的PN序列。PN序列具有良好的自相关性，只有当序列对齐时，才会产生一个极高的相关峰［2］，而如果PN序列未对齐，则理论上相关值趋于0。如图1所示为PN序列的自相关仿真图，可以观察到对齐时有一个极高的相关峰，其余未对齐时刻，相关值很小。

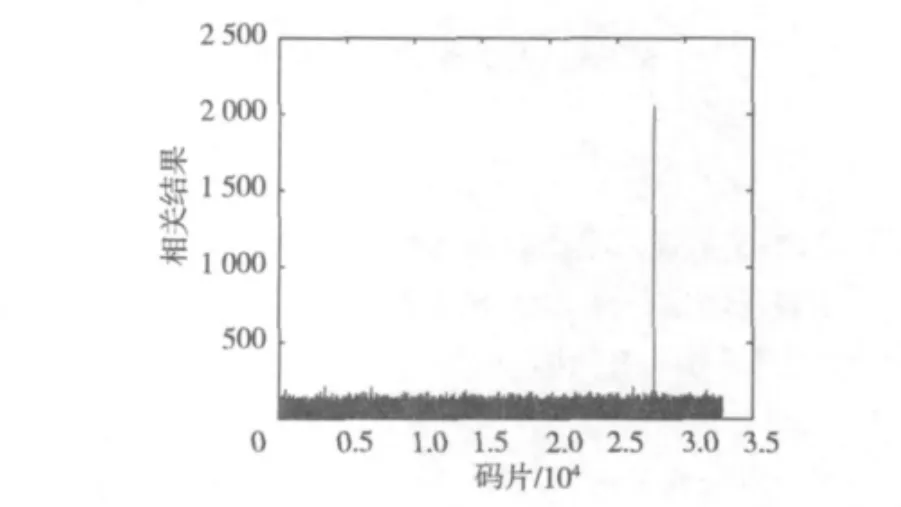
图1 PN序列的自相关特性

1.2 进行相关运算数据长度的确定

如何选择适当的数据长度来完成相关运算是一个比较重要的问题。如果选取数据长度过长，会带来巨大的计算量;而如果选取数据长度过短，则会导致计算结果的精度下降，甚至可能无法正确地完成同步过程。

因此有必要对进行相关运算的数据长度对相关性能的影响进行评估。在此引入一个相关质量指数的概念。定义:相关质量指数=相关结果均值/相关结果峰值。相关质量指数的取值介于0～1，越接近于0，说明相关性能越好;反之，越接近于1，说明相关性能越差。

选取不同长度的实测数据进行相关运算，其对应的相关质量指数如图2所示。

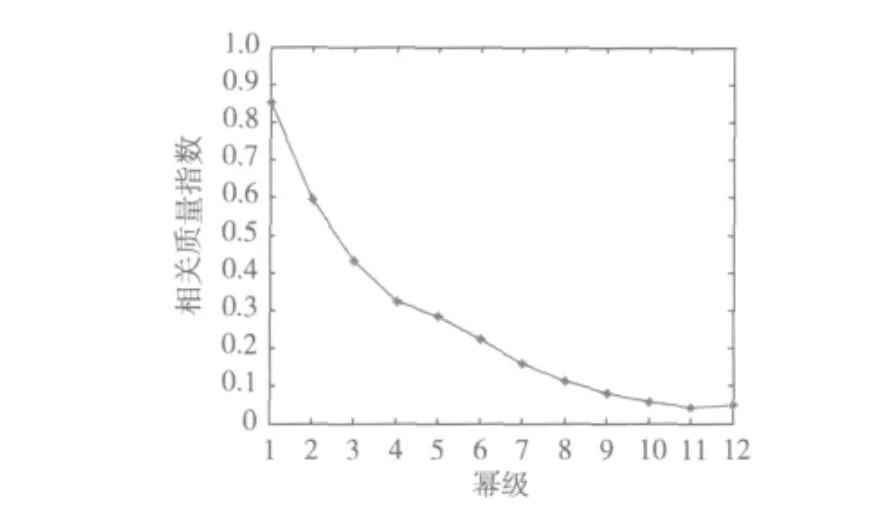
图2 数据长度对相关性能的影响图

图2中，横轴值表示进行相关运算的数据长度的幂级(以2为底)。当进行相关运算的数据长度的幂级为11及更大时，即长度为211=2048码片及以上的时候，已经具有了良好的相关性能，经MATLAB对实测CDMA数据仿真后发现当数据长度为4096时，相关性较好，如图3所示。从图中可以看出有2个相关峰值，峰值明显高于未对齐时所得相关值，该结果完全符合设计要求。

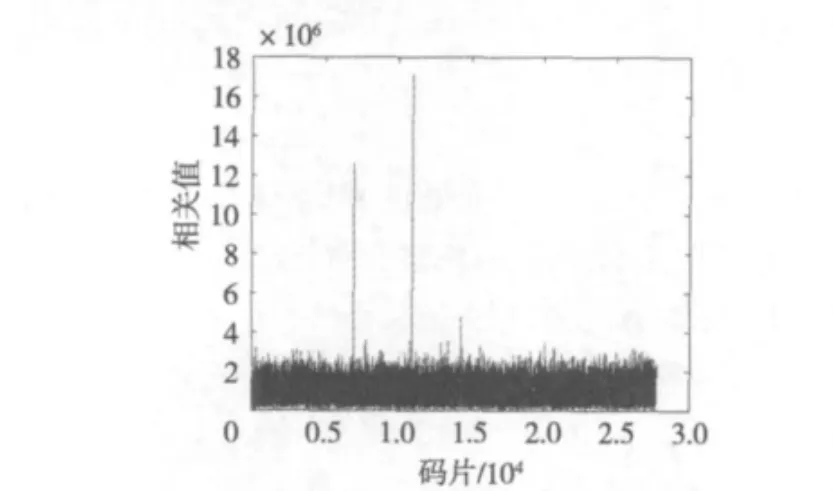
图3 4096码片的相关图

1.3 FPGA实现方案比较和选择

实现前向信道同步的方法很多，常用的搜索法有滑动相关法和使用FFT快速相关的方法。

1.3.1 滑动相关法

对于滑动相关法，即是将PN短码序列x(i)进行延迟并与CDMA前向信道数据y(i)进行相关处理，获得相关峰，从而达到同步的目的。在FPGA中实现时，将序列y(i)保持不变，短序列x(i)不断向右滑动1个点，同时计算在每个位置上，x(i)与y(i)的相关值。如此滑动1个周期后，一定会出现相关峰，相关峰的所在点即是相关点。

使用情况:适合FPGA芯片资源少、对CDMA同步实时性要求不高的系统。

优缺点:该方法实现简单，占用FPGA资源少，但达到同步所花费的时间长。

1.3.2 FFT快速相关法

使用FFT实现快速同步的方法，由式(1)知，可用卷积的方式来实现相关，即

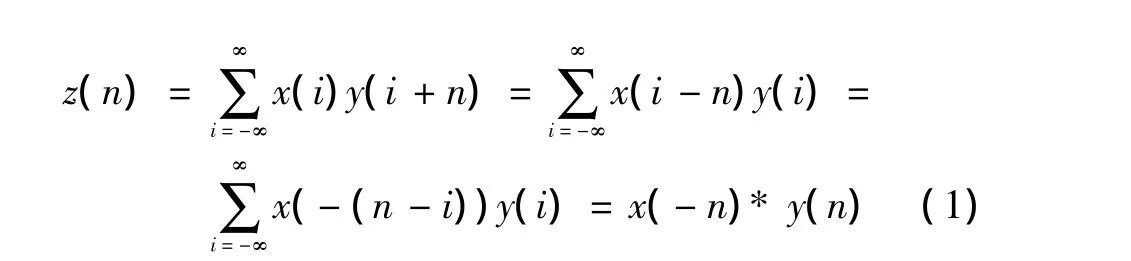
但是使用卷积来实现相关计算量非常庞大。因此，实际中使用快速傅里叶变换方式实现相关［3］，即

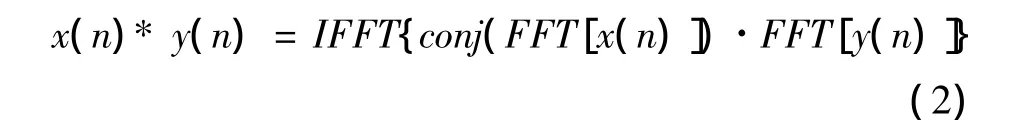
从而能达到快速同步的目的。

其过程如下:

1)选择L满足

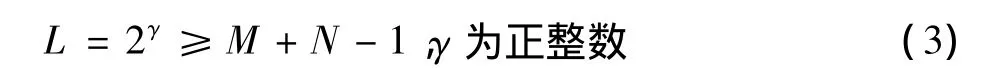
当设计时，选择PN序列长度M为32768，数据长度N为4096，L长度为65536。

2)用x(n)表示PN序列;用y(n)表示CDMA的前向信道数据。

3)将序列x(n)与y(n)按如下方式补0，形成长为L的序列即

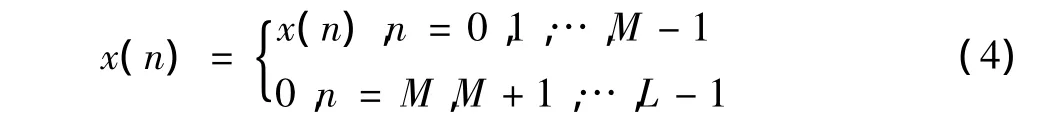
在后面补L-M个0。

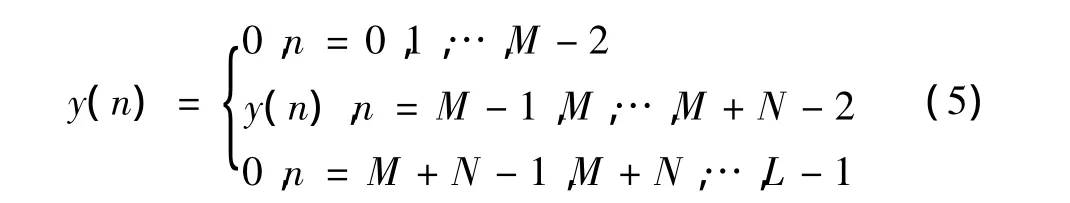
即在前面补M-1个0，在后面补L-(M+N-1)个0。

4)对x(n)与y(n)分别进行FFT运算，结果为X(k)与Y(k)。并将X(k)的复共轭X*(k)与Y(k)相乘，即

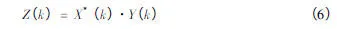
5)对Z(k)进行IFFT运算，结果为z(n)。并截取z(n)的从第N个到第M个值(从1开始)，再将所得结果倒序。

使用情况:适合FPGA芯片资源较多、对CDMA同步实时性要求较高的系统。

优缺点:算法实现较复杂，占用FPGA资源多，但实现同步所需时间短等特点。

基于对实时性要求较高的考虑，本设计选择FFT快速相关法，参数:PN码长度M为32768，数据长度N为4096，FFT变换长度为65536。按此方案进行粗略计算，如果系统时钟为100 MHz时，当使用滑动相关法时，从系统接收完所需长度(4096)的实时CDMA数据后，至少需要2.51 s才能找到同步位置，可见如此长的时间是很多系统所无法容忍的;当使用FFT快速相关法时，PN码的FFT变换在上电之后先完成，所以其时间不需要计入同步花费时间内，在接收完所需长度(4096)的CDMA数据后，达到同步所需时间仅为4 ms左右，是滑动相关法所需时间的1/600。由此可见，FFT快速相关法在时间开销上的优越性。

2 FPGA实现流程

2.1 流程分析

整体设计流程图如图4所示，数据由中频经过14 bit数据I/O口在控制信号下进入基带数据收发模块，抽取处理后在IFFT/FFT变换模块进行FFT变换，变换后数据在数据运算模块和已经过FFT变换的复共轭PN码进行点乘，之后传回IFFT/FFT变换模块进行IFFT变换，其结果在同步位置判定模块中进行平方求其最大值。

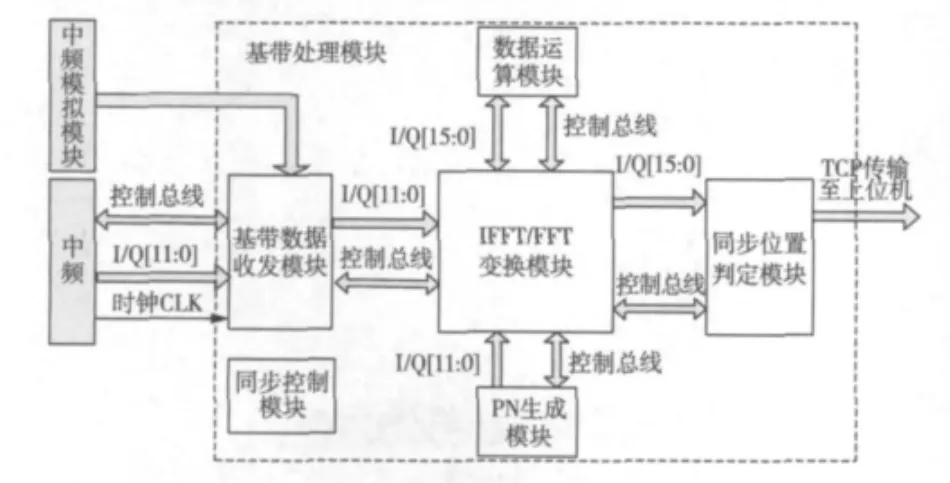
图4 整体设计流程框图

2.2 模块解析

1)同步控制模块

通过模块对同步结果进行分析，判定该结果是否有效。当无效时，则再进行一次同步运算，一直到符合所设参数要求为止。

2)PN码生成模块

在CDMA系统中，双极性PN短码分为I，Q两路，由1和-1组成，它们的生成多项式为

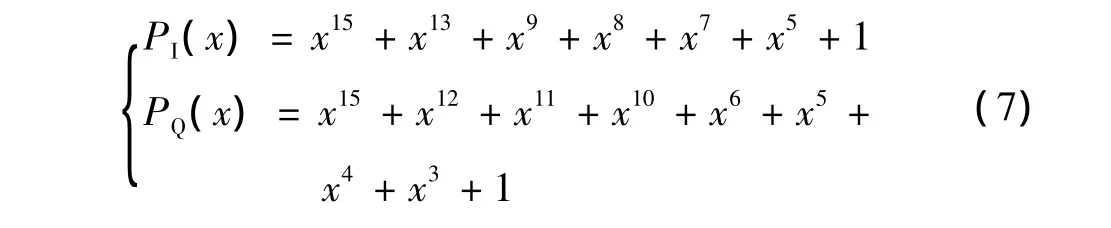
在FPGA中实现时，主要以移位和异或相结合的方式来产生PN短码。

3)基带数据收发模块

本文中仿真所使用到的数据均采用了4倍采样I和Q两路，由于CDMA的码片速率为1.2288 Mchip/s(兆码片/s)［4］，则基带接收数据时钟CLK应该为9.8304 MHz。基带数据收发模块在中频数据有效信号有效时，在时钟CLK的同步下4倍抽取中频传输的基带数据用于同步处理，并存放于异步FIFO中，以达到不同时间域的同步。为记录数据接收的起始位置，在数据接收时，拉高dump信号一个时钟周期，作为数据起始的标志位，为以后对数据进行接收的开始标志。同时用一个周期为32768×4(CDMA导频信道中传输的数据周期)的加法器进行循环累加，计完一个周期，拉高一次dump信号。基带数据传输到IFFT/FFT变换模块时，需要有与数据同步拉高的data_source_valid信号，从而使数据能被正确接收。

4)IFFT/FFT变换模块

IFFT/FFT变换模块主要实现对基带数据和PN码先后进行FFT变换，并对其点乘后的数据进行IFFT变换。为提高开发效率，减小设计风险，因此选用Altera官方提供的FFT IP核［5］。为节约FPGA片内资源，只调用一个FFT核，其参数为:变换长度(Transform Length)为65536;数据精度(Data Precision)为16 bit;数据流模式(I/O Data Flow)为突发模式(数据吞吐量相比较小但占用资源少);其他选项选择为默认。从IP核配置界面中可知，此参数配置下，占用Memory Bits为4112384，因此对芯片的资源要求很高。

由于同一时刻，FFT IP核只能处理某段数据流，且考虑到数据的实时性和连续性，所以控制好数据流进入FFT IP核的时机和顺序非常重要。因此，本模块中采用状态机和握手信号来完成。

由于PN码由值很小的+1和-1组成，而FFT核对值小的数据处理时，其结果也相对很小，甚至会导致结果出错，因此，设计中将PN码的值扩大500倍，即变为+500和-500。经ModelSim仿真，其结果和MATLAB仿真结果幅度变化一致，且幅值符合要求。

5)数据运算模块

数据运算模块主要实现复共轭点乘Z(k)=X*(k)Y(k)，可以调用 ALTMULT_COMPLEX IP 核［6］，其可以稳定快速地完成此运算，运算结果再传输到IFFT/FFT变换模块中进行IFFT反变换。由于X(k)和Y(k)不是同时输入，因此需要用FIFO暂存X(k)数据，当Y(k)输入时，再从FIFO中读取出和Y(k)同步输入到ALTMULT_COMPLEX IP核中。

6)同步位置判定模块

同步位置依次判定从模块IFFT/FFT变换模块中输出的IFFT反变换结果，对其进行求平方取模，对模值逐一比较大小，保留最大值的位置和值的大小，再推算出同步的位置。

7)中频模拟模块

本模块独立于基带处理模块，单独用一块板子来达到模拟中频数据源的目的。它通过USB接口接收PC机发送的CDMA数据，FPGA通过控制USB芯片将数据接收放入FIFO中，再通过I/O口传输到基带处理模块的FPGA中。该模块选用了Alteral的EP3C25Q240C8的FPGA芯片，该芯片具有很高的性价比，而且资源丰富。同时，还选用CY7C68013的USB芯片以实现USB通信。

3 FPGA实现结果及分析

3.1 功能仿真结果分析

完成Verilog代码编写后，运用ModelSim对上述模块进行仿真，使仿真结果符合设计要求。图5为PN码生成模块产生PN码的仿真时序图，shift_reg_i和shift_reg_q为初始相位(0x8000)，pn_code_i和pn_code_q分别为I，Q两路的PN码(16 bit)，其产生结果符合设计要求。在输出PN码到IFFT/FFT变换模块的同时，out_state信号拉高，表明PN短码有效，作为其他模块接收该PN码的同步信号。

图5 PN码仿真时序图(截图)

图6为IFFT/FFT变换模块的时序仿真图，为简化控制时序的验证，FFT长度采用1024，经验证，时序符合设计要求。输入信号中，sink_real和sink_imag为FFT模块输入的实部和虚部，sink_valid为输入数据有效信号，inverse置0时，表示FFT模块执行的是FFT变换，置1时，该模块执行FFT反变换，而输出信号source_real和source_imag为FFT核变换后输出数据，source_valid为输出数据有效信号。从图6中可以观察到有3段进入到FFT核的数据流，分别为PN码x(n)、CDMA数据y(n)和它们FFT变换点乘后的数据z(n)，可以看出时序符合FFT核的要求。

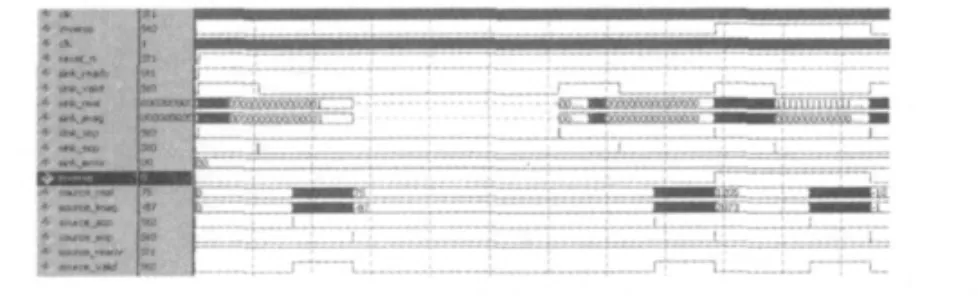
图6 FFT/IFFT仿真时序图(截图)

3.2 数据位宽确定

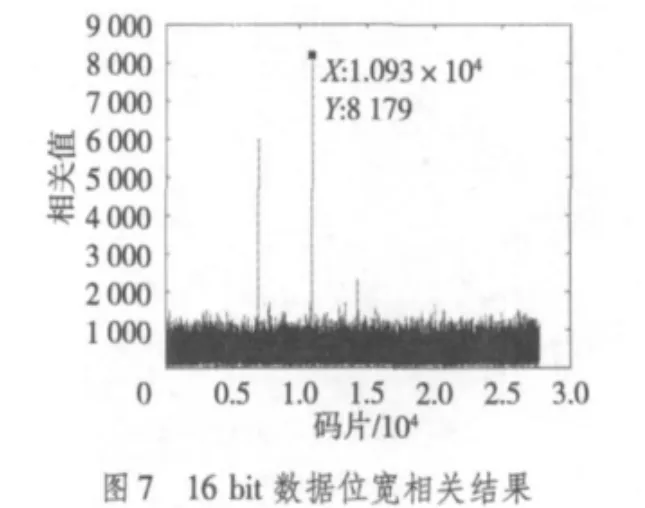
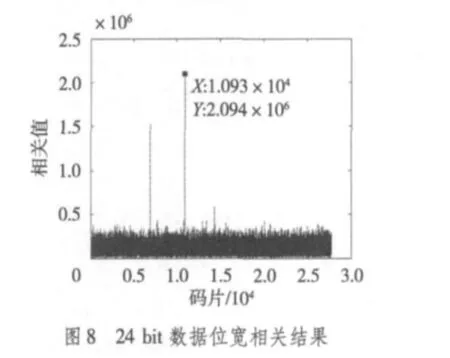
在数据运算模块中，将进行数据(16 bit)点乘运算，其结果导致数据位宽将会增大一倍(32 bit)，因此有必要进行数据截取。数据位太宽，会占用过多的资源，而数据精度太低时，会影响数据结果，甚至会导致出错。本文中在16 bit和24 bit数据位宽两种情况下进行整个同步模块的ModelSim仿真，并将相关的结果值用MATLAB绘图，其结果如图7和图8，虽然24 bit的数据均值是16 bit的256倍，但MATLAB计算得出两种位宽的峰均比分别为13.28和13.29，几近相等。可以知道，由于CDMA PN码良好的相关性，只要数据位宽足够，24 bit宽的数据只是在16 bit宽数据的基础上增大256倍，但并不影响峰值点的确定。如果在相关性没这么好的GSM系统中进行同步处理时，如果数据位宽不够，会导致同步位置偏移几个点，而在CDMA中影响不大。因此，本文中数据位宽选择16 bit。

3.3 FPGA程序正确性验证

为验证用Verilog编程的程序算法思想的正确性，将Verilog编写的每个模块所生成的数据和用MATLAB仿真产生数据相对比，判定结果是否一致。图3为用MATLAB仿真的结果，可以看到有3个相关峰(最大峰值的峰均比为13.30)，这是由空中截取的CDMA信号包含了相邻基站的导频信息所致。但是由于移动终端一般接入最强导频的基站，本文以最高相关峰为当前服务基站的同步点。而用ModelSim仿真得到的相关数据用MATLAB绘制结果如图7和图8，峰均比为13.28和13.29，且得出的同步点和MATLAB的仿真结果一致。因此，用FPGA实现CDMA的短码同步是可行的。

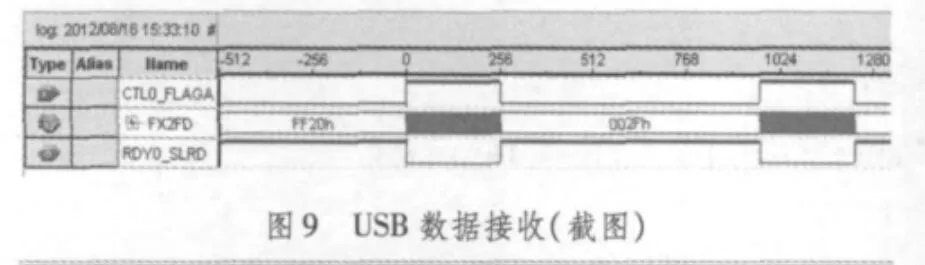
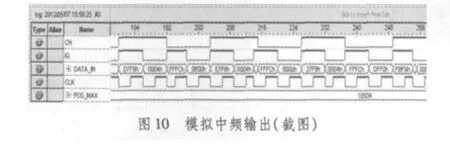
经过仿真验证后，进行了板级调试，并用逻辑分析仪观察FPGA芯片内部信号和输出信号。图9为Cyclone III芯片接收USB芯片发送的CDMA数据，CTLO_FLAGA为信号输出有效信号，FX2FD为接收的数据，每次接收收据大小512 byte，该大小可以通过程序更改。图10为Stratix II芯片的调试结果，POS_MAX为最大峰值的相位，可以看出该值和之前仿真的结果一致。

4 小结

本文提出了CDMA下行同步算法，设计了基于Verilog的同步算法模块，并利用ModelSim对各个模块进行仿真，并将运算结果和MATLAB仿真结果进行对比，其结果一致。由于PN码良好的相关性，经过仿真可以得出，在数据位宽为16 bit和24 bit时，虽然得出的数据值不一样，但最终的峰均值却几近相等，因此，为节约FPGA芯片资源，将数据位宽确定为16 bit。最终，经过板级调试和验证，性能稳定可靠，说明该同步算法是可行的。

［1］徐海燕，田增山，沈建国，等.基于CDMA2000移动目标的探测方法研究［J］.重庆邮电大学学报:自然科学版，2008(1):36-38.

［2］OK K M，KANG C G.Generalized window-based PN acquisition scheme in CDMA2000 spread spectrum systems［C］//Proc.Global Telecommunications Conference.［S.l.］:IEEE Press，2005:1530-1534.

［3］殷福亮，宋爱军.数字信号处理C语言程序集［M］.沈阳:辽宁科学技术出版社，1997.

［4］ROSE G，KOIEN G M.Access security in CDMA2000，including a comparison with UMTS access security［J］.IEEE Wireless Communications，2004，11(1):19-25.

［5］Altera corporation.FFT MegaCore FunctionuserGuide［EB/OL］.［2012-07-10］.http://www.altera.com/literature/ug/ug_fft.pdf.2011.

［6］Altera corporation.Integer arithmetic mega functions user guide［DB/OL］.［2012-07-10］.http://www.altera.com/literature/ug/ug_lpm_alt_mfug.pdf.2010.