A New Kind of Iteration Method for Finding Approximate Periodic Solutions to Ordinary Differential Equations
2013-08-10WUDONGXUWANGCAILINGANDXUXU
WU DONG-XU,WANG CAI-LINGAND XU XU
(1.Department of Applied Mathematics,School of Science,Changchun University of Science and Technology,Changchun,130022) (2.School of Mathematics,Jilin University,Changchun,130012)
Communicated by Li Yong
A New Kind of Iteration Method for Finding Approximate Periodic Solutions to Ordinary Differential Equations
WU DONG-XU1,WANG CAI-LING2AND XU XU2
(1.Department of Applied Mathematics,School of Science,Changchun University of Science and Technology,Changchun,130022) (2.School of Mathematics,Jilin University,Changchun,130012)
Communicated by Li Yong
In this paper,a new kind of iteration technique for solving nonlinear ordinary differential equations is described and used to give approximate periodic solutions for some well-known nonlinear problems.The most interesting features of the proposed methods are its extreme simplicity and concise forms of iteration formula for a wide range of nonlinear problems.
iteration method,approximate periodic solution,ordinary differential equation
1 Introduction
In this paper we deals with the approximate solutions to the equations of the following form u′′+a(t)u′+b(t)u=f(t,u,u′),(1.1) where a(·),b(·)and f(·,u,u′)are T-periodic in t.
From the point of view of physical applications,as well as from the point of view of theory,it is very important to know how to solve the equation(1.1).
Inspired by the constant variation formula,we present a new kind of iteration method for finding approximate solutions of the equation above.The method will be shown to solve a large class of nonlinear problems effectively,easily and accurately.
Before providing our iteration procedure,two other nonlinear analytical methods:“variational iteration method(VIM)”developed by He in[1–8]and“Adomian decompositionmethod(ADM)”developed by Adomian in[9–10]are mentioned.The two methods,which accurately compute the solutions in a series form or in an extreme form,are of great interesting to applied sciences.Wazwaz[11]raised the method FOR to detail the VIM and ADM, and a comparison between them.In particular,the issue 207 of Journal of Computational and Applied Mathematics consists of a collection of recently obtained results and various new interpretation of earlier conclusions pertinent to the application of the VIM for real-life nonlinear problems.
Our method seems more efficient than VIM and ADM.Furthermore,there is no any secular term in the computation.
The layout of the paper is as follows:In Section 2,we give the main idea of the method and the iteration procedure.In Section 3,several examples are given to illustrate the effectiveness of our method.
2 Iteration Procedure
Consider the equation(1.1).Let φ1(t),φ2(t)be two fundamental solutions with φ1(0)=1,=1.Set
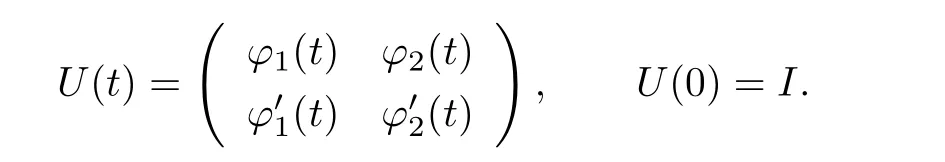
Assume that x(t)is a T-periodic solution of the equation(1.1).Then
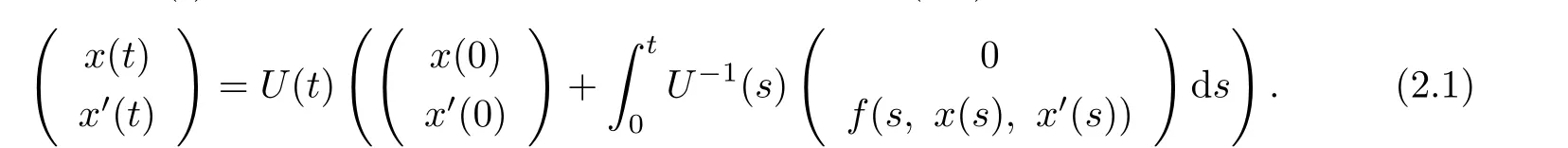
Since

one has
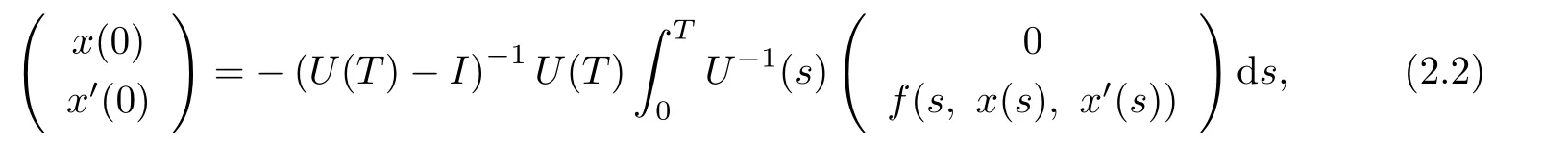
provided U(T)-I is non-singular.
Now substituting(2.2)into(2.1),we have
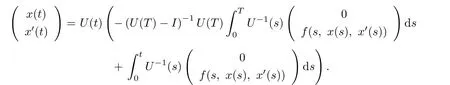
Let
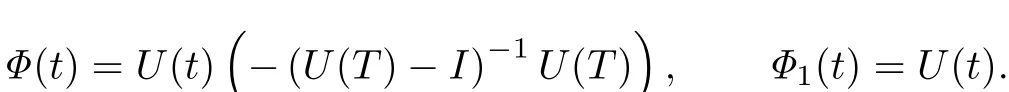
Then
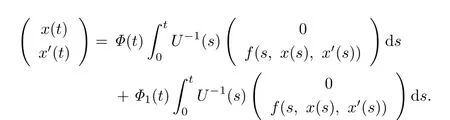
Now,we give the iteration formula as follows:
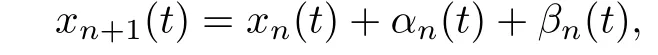
where αn(t)is the first component of
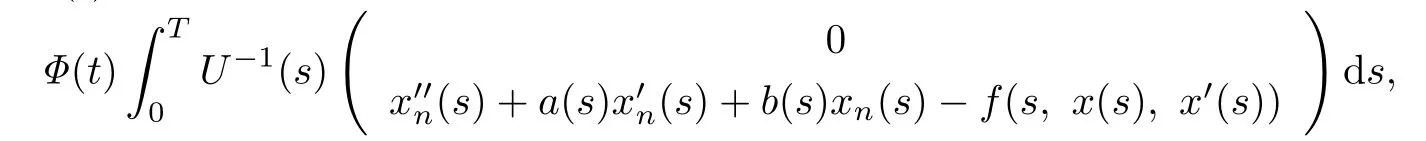
and βn(t)is the first component of
(
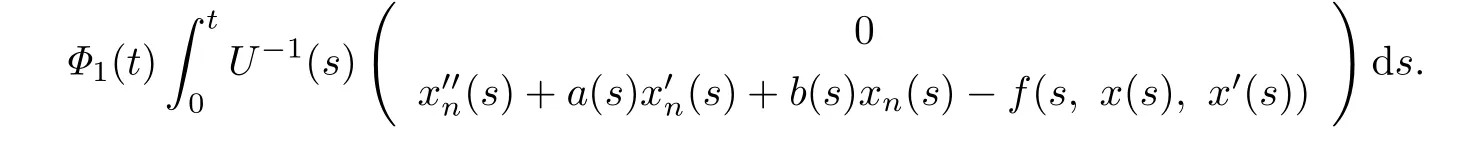
3 Examples
Example 3.1Consider the Van der Pol-Duffing equation
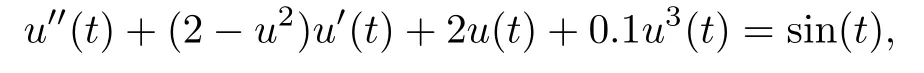
i.e.,
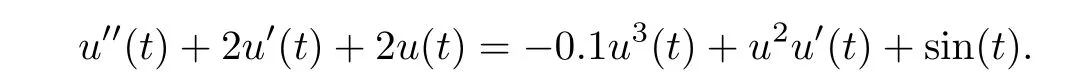
Its fundamental solution matrix is

Initial approximation:
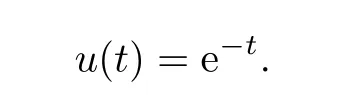
The approximation of the first time(shown in Fig.3.1):

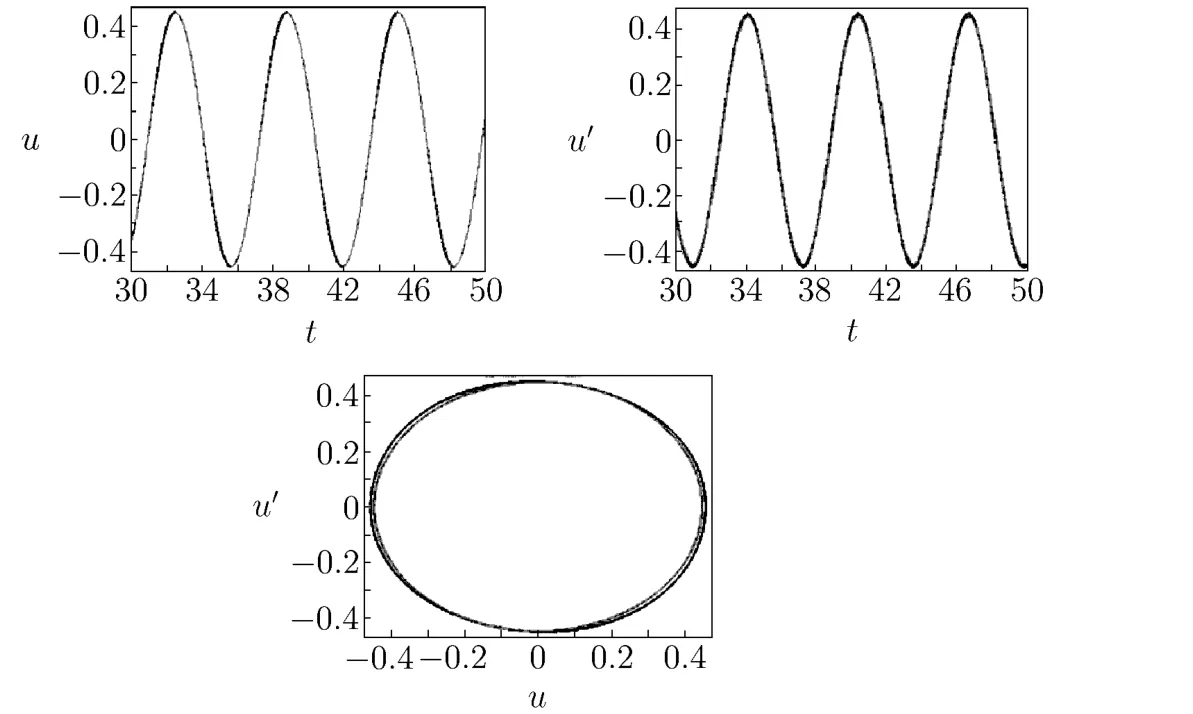
Fig.3.1
The approximation of the second time(shown in Fig.3.2):
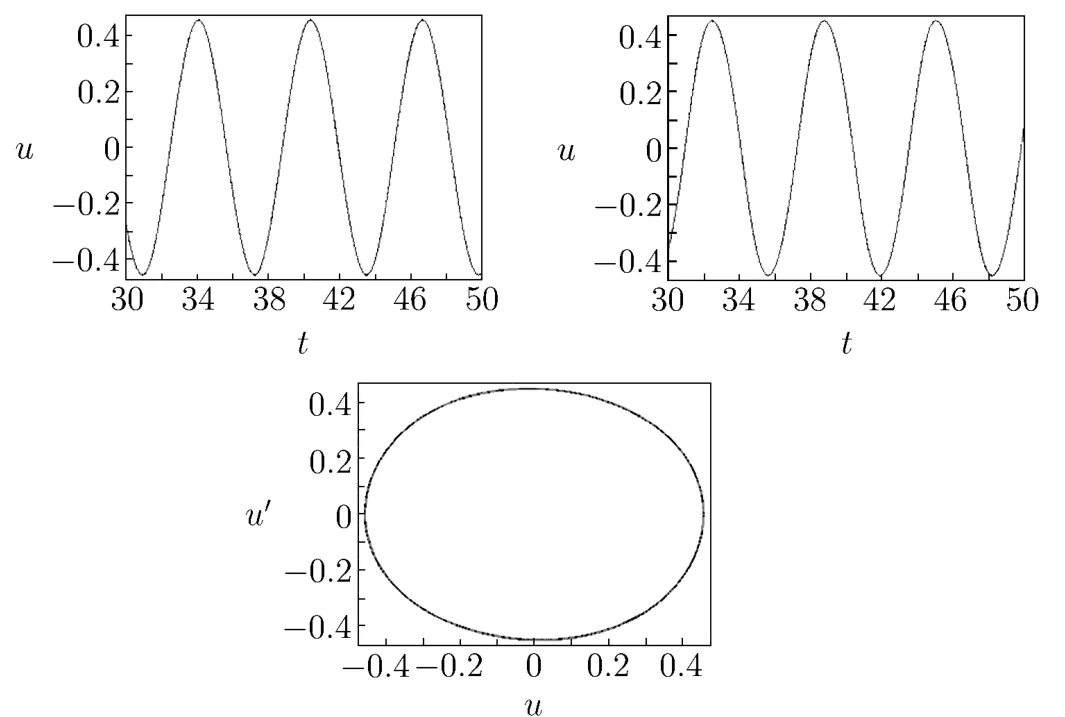
Fig.3.2
Example 3.2Consider the equation
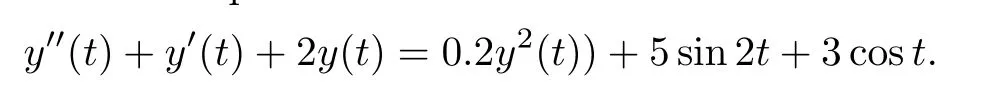
Its fundamental solution matrix is
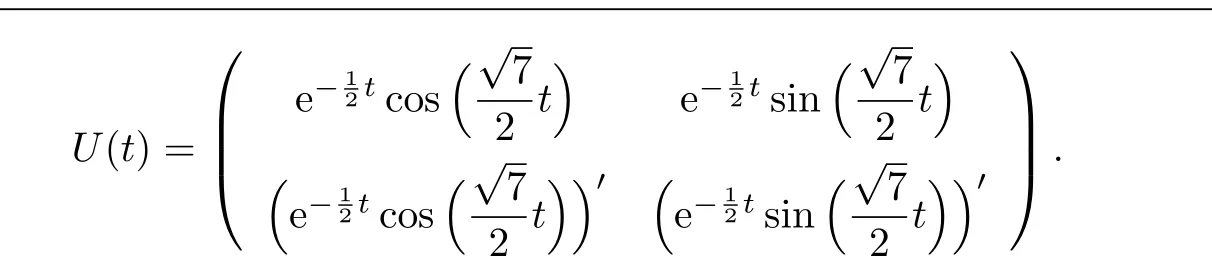
The approximation of the first time(shown in Fig.3.3):

Initial approximation:
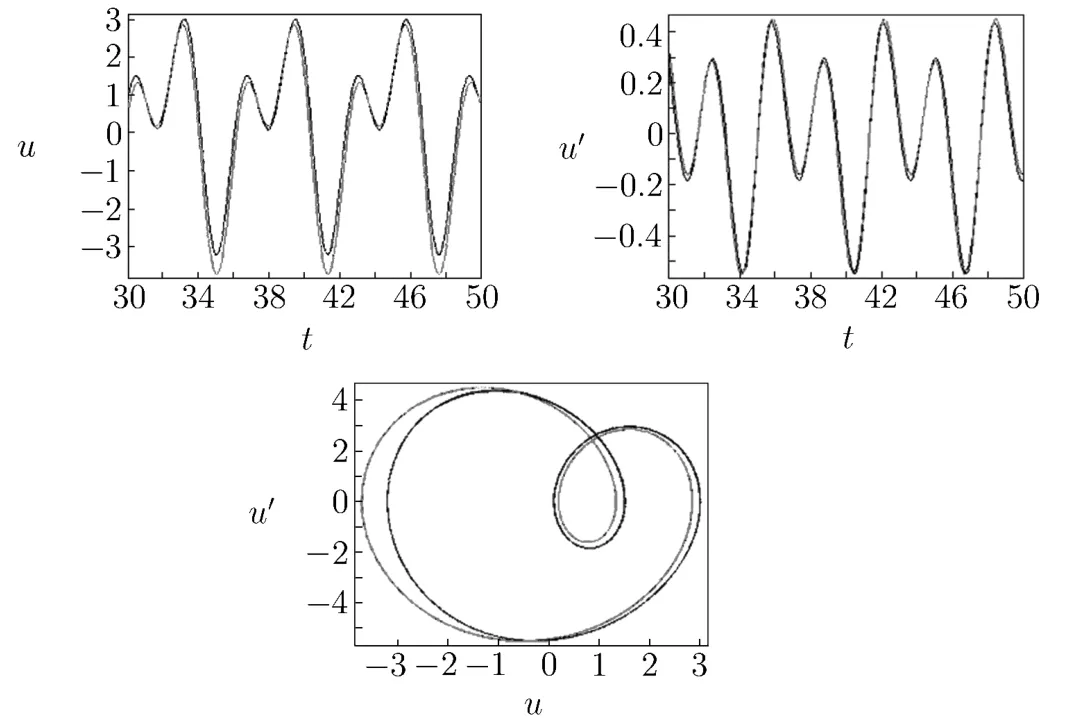
Fig.3.3
The approximation of the second time(shown in Fig.3.4):


Example 3.3Consider the strong nonlinear Duffing equation
Its fundamental solution matrix is

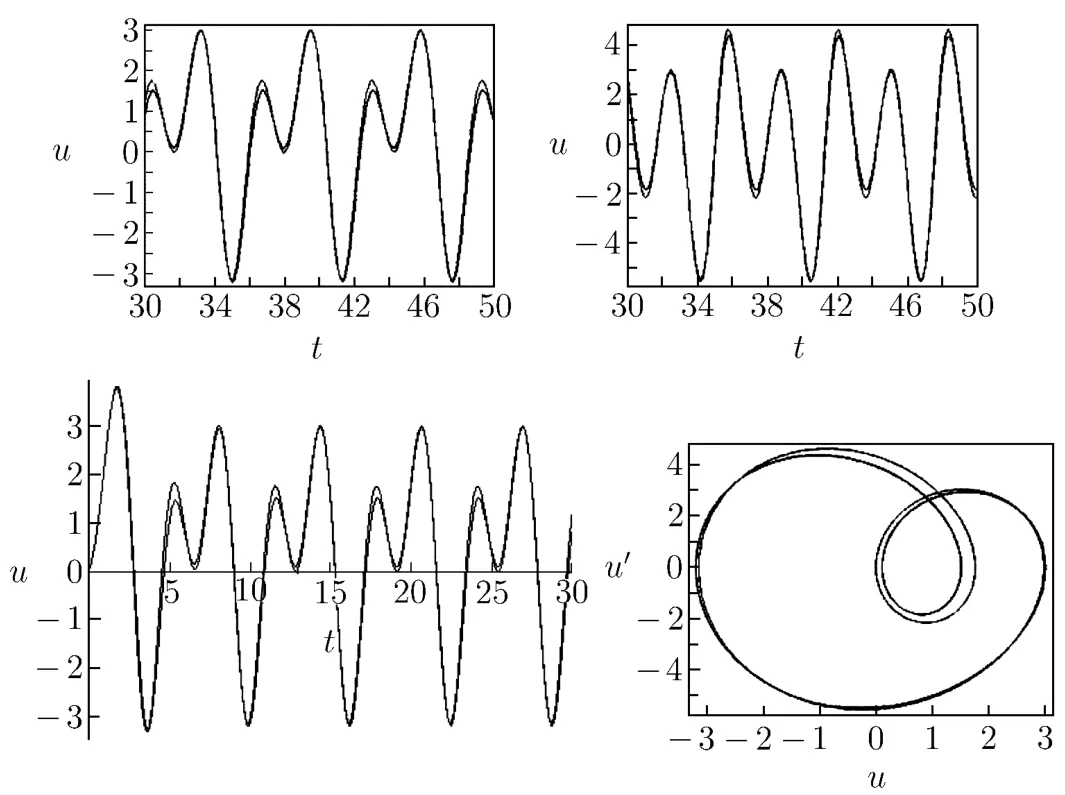
Fig.3.4
Initial approximation:
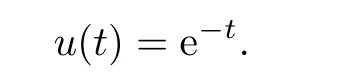
The approximation of the first time(shown in Fig.3.5):
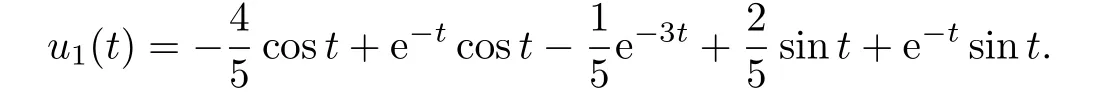
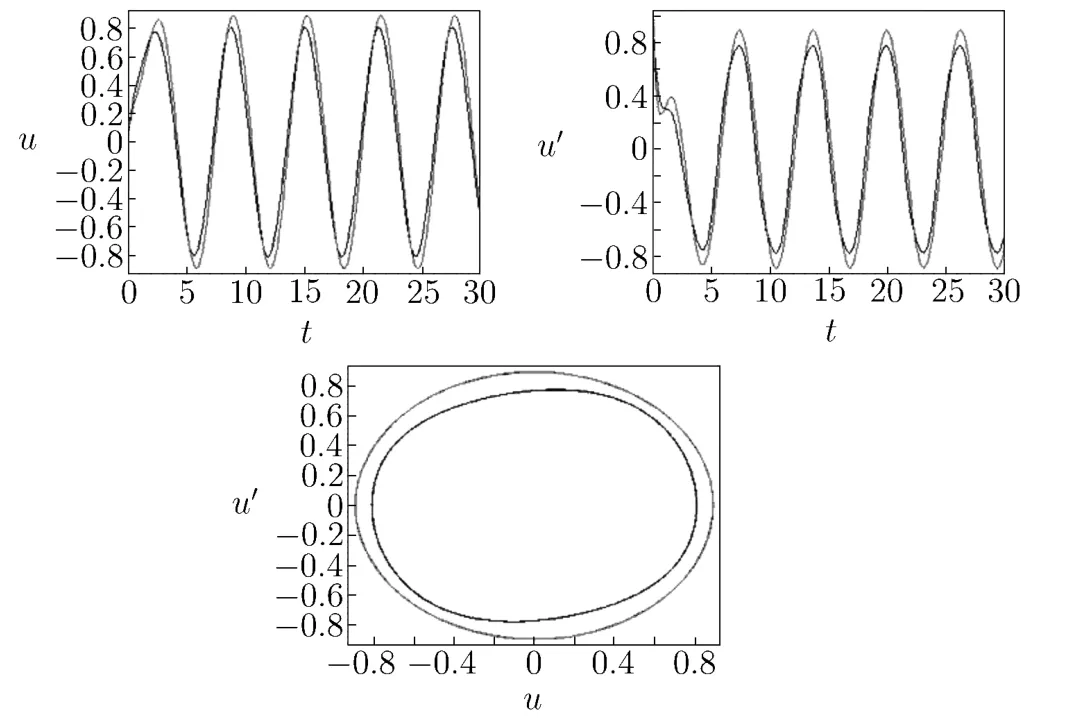
Fig.3.5
The approximation of the second time(shown in Fig.3.6):
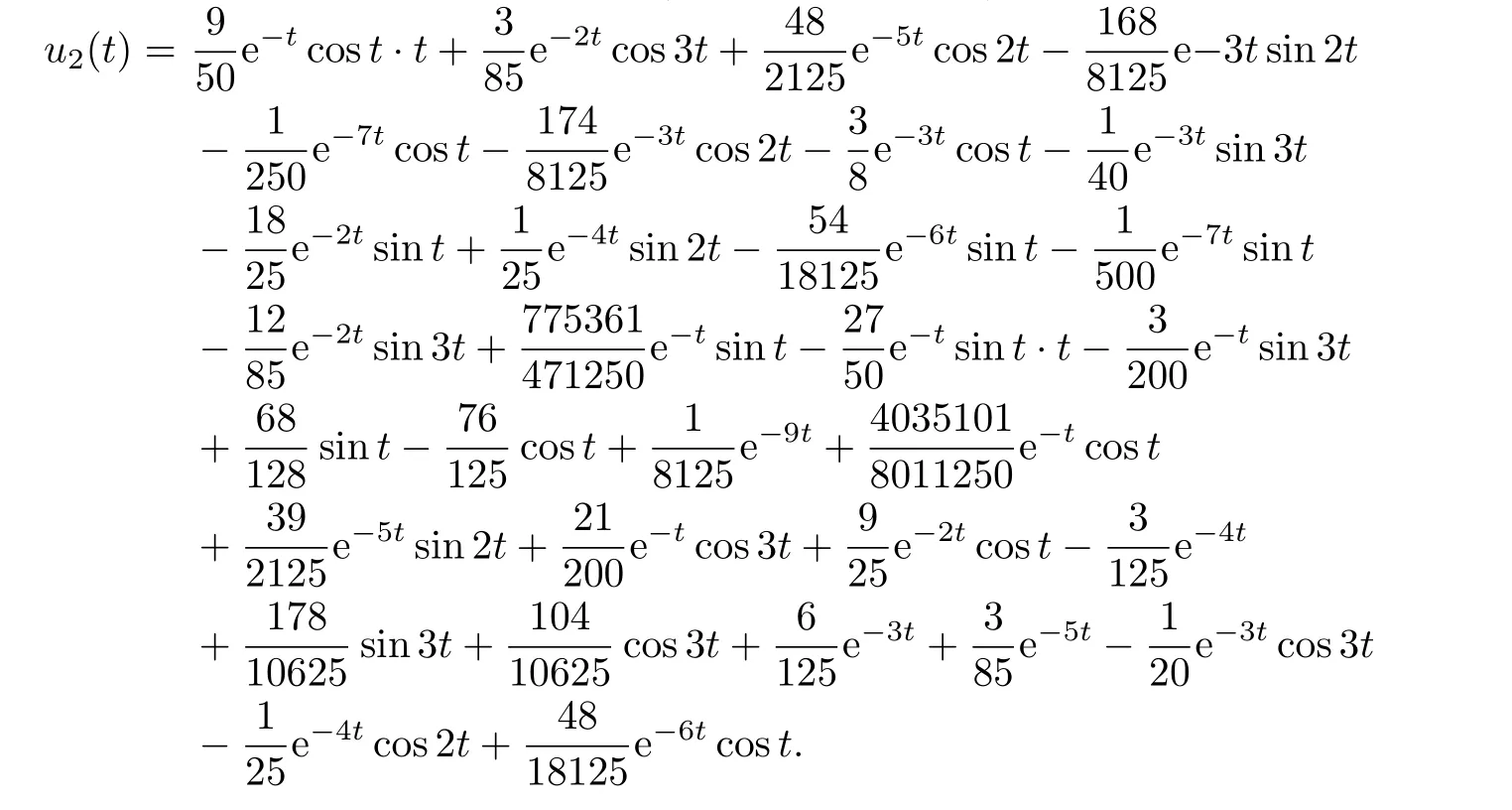
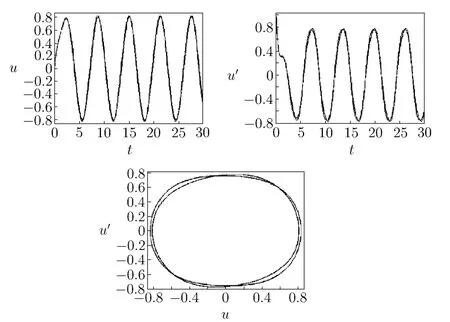
Fig.3.6
[1]He J H.A new approach to nonlinear partial differential equations.Commun.Nonlinear Sci. Numer.Simul.,1997,2(4):203–205.
[2]He J H.Approximate analytical solution for seepage f l ow with fractional derivatives in porous media.Comput.Methods Appl.Mech.Engrg.,1998,167:57–68.
[3]He J H.A variational iteration approach to nonlinear problems and its applications.Mech. Appl.,1998,20(1):30–31.
[4]He J H.Variational iteration method,a kind of nonlinear analytical technique:some examples. Internat.J.Non-Linear Mech.,1999,34:708–799.
[5]He J H.Variational iteration method for autonomous ordinary differential systems.Appl.Math. Comput.,2000,114(2/3):115–123.
[6]He J H.Homotopy perturbation method:a new nonlinear technique,Appl.Math.Comput., 2003,135:73–79.
[7]He J H.Some asymptotic methods for strongly nonlinear equations.Internat.J.Modern Phys. B,2006,20(10):1141–1199.
[8]He J H.Non-perturbative Methods for Strongly Nonlinear Problems,Dissertation.Berlin: de-Verlag im Internet GmbH,2006.
[9]Adomian G.A review of the decomposition method in applied mathematics.J.Math.Anal. Appl.,1988,135:501–544.
[10]Adomian G.Solving Frontier Problems of Physics:The Decomposition Method.Boston: Kluwer Academic Publishers,1994.
[11]Wazwaz A.A comparison between the variational iteration method and Adomian decomposition method.J.Comput.Appl.Math.,2007,207(1):129–136.
35A15,34A34,34B15,34C15
A
1674-5647(2013)04-0297-08
Received date:Dec.10,2009.
E-mail address:dxwu19810712@163.com(Wu D X).
杂志排行
Communications in Mathematical Research的其它文章
- Stability of Cubic Functional Equation in Three Variables
- The First Initial Boundary Value Problem for Parabolic Hessian Equations on Riemannian Manifolds
- A Gorni-Zampieri Pair of a Homogeneous Polynomial Map
- Principal Quasi-Baerness of Rings of Skew Generalized Power Series
- On Results the Growth of Meromorphic Solutions of Algebraic differential Equations
- A Class of Regular Simple ω2-semigroups-II
