Stability of Cubic Functional Equation in Three Variables

YANG A-LI AND CHENG LI-HUA

(School of Science,Xi'an Polytechnic University,Xi'an,710048)

Communicated by Ji You-qing

Stability of Cubic Functional Equation in Three Variables

YANG A-LI AND CHENG LI-HUA

(School of Science,Xi'an Polytechnic University,Xi'an,710048)

Communicated by Ji You-qing

In this paper,we prove a generalization of Hyers'theorem on the stability of approximately additive mapping and a generalization of Badora's theorem on approximate ring homomorphism.We also obtain more general stability theorem, which gives stability theorems on Jordan and Lie homomorphisms.The proofs of the theorems in this paper are given following essentially the Hyers-Rassias approach to the stability of the functional equations connected with Ulam's problem.

stability,functional equation,Lie homomorphism

1 Introduction

In 1960,Ulam[1]raised the following question concerning the stability of homomorphisms:

Ulam's QuestionLet G1be a group and G2be a metric group with a metric d(·,·). Given any ε＞0,it exists a δ＞0 such that if a mapping f:G1→G2satisfies

then there is a homomorphism g:G1→G2with

The first result in this direction is proved by Hyers[2]which established the stability of a group homomorphism.

Theorem 1.1[2]Let ε≥0 and f be a function defined on an Abelian group(G,+)with values in a Banach space(Y,‖·‖)satisfying

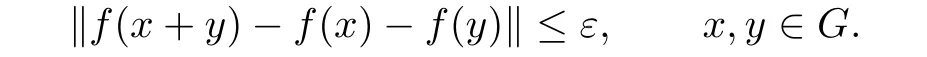
Received date:Oct.11,2009.

E-mail address:yangali0206@126.com(Yang A L).

Then there exists a unique additive mapping h:G→Y,such that

In 1978,Rassias[3]provided the following drastic generalization of Hyers's result which allows the Cauchy difference to be unbounded.

Theorem 1.2[3]Consider E1,E2to be two Banach spaces,and let f:E1→E2be a mapping such that f(tx)is continuous in t for each fixed x.Assume that there exist θ≥0 and p∈[0,1)such that

Then there exists a unique linear mapping T:E1→E2such that

Badora[4]proved the following result concerning the stability of a ring homomorphism:

Theorem 1.3[4]Let R be a ring,B be a Banach algebra,and ε,δ≥0.Assume that f:R→B satisfies

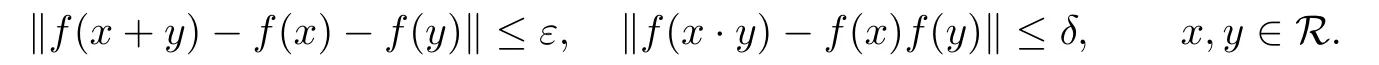
Then there exists a unique ring homomorphism h:R→B such that

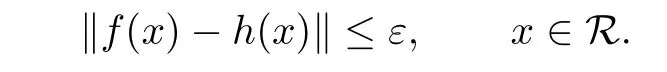
During the last decades,Hyers'theorem has been generalized in various directions(see [5–13]).In this paper,we generalize Hyers'theorem and Badora's theorem above.Based on these,we give a stability theorem both on Jordan homomorphism and on Lie homomorphism.

2 Stability of Approximate Group Homomorphisms

We first prove a theorem on stability of approximate group homomorphisms,which generalizes Hyers'theorem.

Jun and Kim[14]introduced the following functional equation:

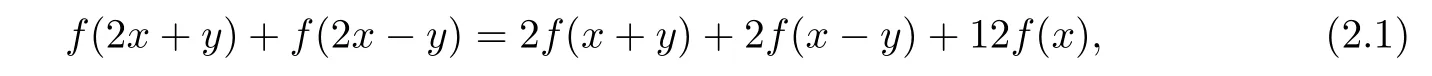
and they established the general solution and the generalized Hyers-Ulam-Rassias stability problem for(2.1).

Park and Jung[15]introduced the functional equation

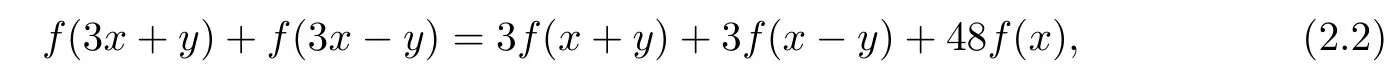
and they established the general solution and the generalized Hyers-Ulam-Rassias stability problem for(2.2).

Later,Najati and Moradlou introduced two functional equations(see[16–17])and they established the general solution and the generalized Hyers-Ulam-Rassias stability problem for(2.4).

It is easy to see that the function

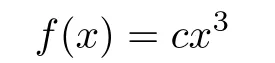
is a solution of(2.1)–(2.3).Thus,these equations are called a cubic functional equations and every solution of them is said to be a cubic mapping.

In this paper,we introduce the following new functional equations

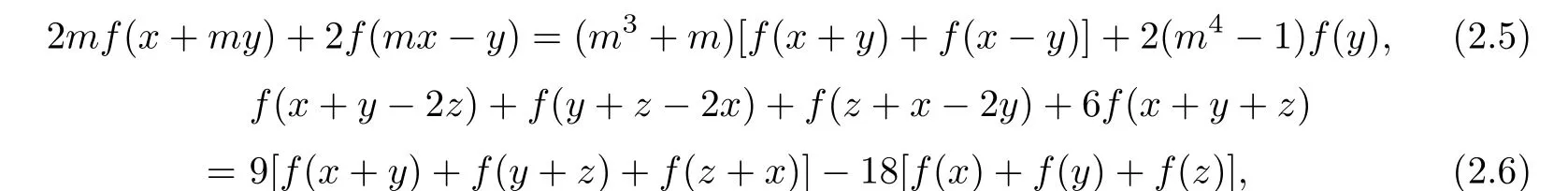
which are somewhat different from(2.1)–(2.3).Obviously,(2.1)and(2.2)are the special case of(2.3),(2.4)is the special case of(2.5),and we establish the general solution and the generalized Hyers-Ulam-Rassias stability problem for the Euler-Lagrange type cubic functional equations(2.5)and(2.6).

3 Stability of Approximate Group Homomorphisms

In this section,we use the fixed point theorem of the alternative for contractions on a generalized complete metric space to prove the stability of the cubic functional equation.

Theorem 3.1[18]Let f:E1→E2be a mapping.The following statements are equivalent:

(i)f satisfies(2.1);

(ii)f satisfies(2.3);

(iii)there exists a function B:E1×E1×E1→E2such that f(x)=B(x,x,x)for all x∈E1,and B is symmetric for each fixed one variable and additive for each fixed two variables.

Theorem 3.2Let f:E1→E2be a mapping.The following statements are equivalent:

(i)f satisfies(2.1);

(ii)f satisfies(2.2);

(iii)f satisfies(2.3);

(iv)f satisfies(2.4);

(v)f satisfies(2.5);

(vi)f satisfies(2.6);

(vii)there exists a function B:E1×E1×E1→E2such that f(x)=B(x,x,x)for all x∈E1,and B is symmetric for each fixed one variable and additive for each fixed two variables.

Proof.From Theorem 3.1,we get that(i),(iii)and(vii)are equivalent.So,if we can show that(iii)⇒(ii),(ii)⇒(i),(iii)⇔(v),(v)⇒(iv),(iv)⇒(ii),(iii)⇒(vi),(vi)⇒(ii),then the theorem would be proved.

Now we assume that(vii)holds.Since a/=1,putting x=y=0 in(2.3),we get

Replace y by 0 and-2x in(2.3),respectively,we get

So the mapping f is odd.

(iii)⇒(ii).Let a=3 in(2.3),we get(2.2).

(ii)⇒(i).Replacing y by y-x and y+x in(2.2),respectively,we have

Similarly,adding(3.1)to(3.2),we get

Noticing that f(mx)=m3f(x),we get(2.1).

(iii)⇒(v).Replacing y by ay in(2.3),we get

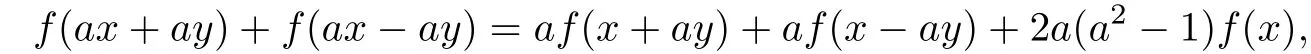
and using the property of f(mx)=m3f(x),we obtain

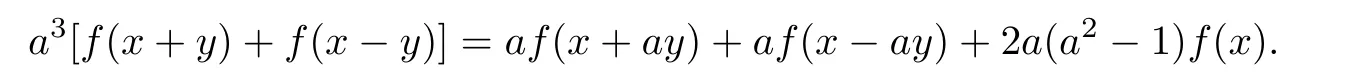
Adding equations(2.1)and(2.3),we get

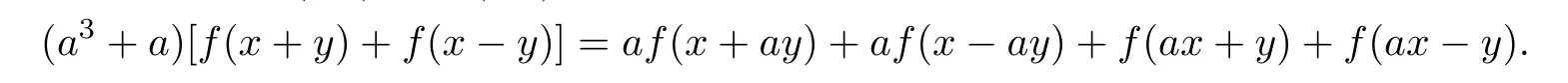
So(2.5)holds if and only if

Replacing x by-y and y by x in(2.3),respectively,and multiplying both sides by a,we get

Adding(3.3)and(3.4),we get(2.5).

(v)⇒(iii).Replacing x by-y and y by x in(2.5),respectively,and using the oddness of f,we get

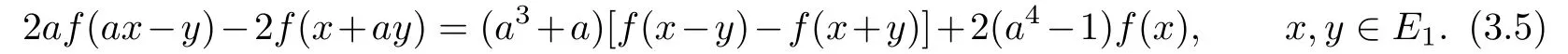
Multiplying both sides of(3.5)by a,and adding the obtained functional equation to(2.5), we get

Replacing y by-y in(3.6)and using the oddness of f,we get

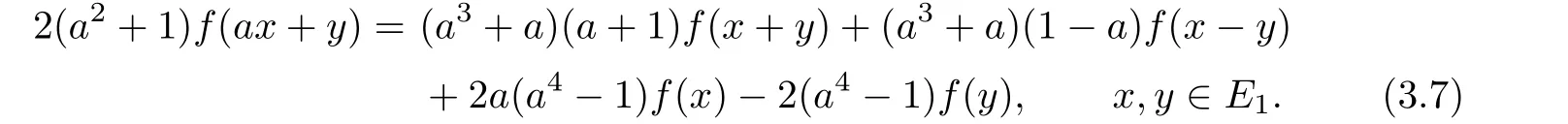
Adding(3.6)to(3.7),we get

Dividing both sides of(3.8)by a2+1,we get(2.3).Therefore(iii)holds.

(v)⇒(iv).Let m=3 in(2.5)and dividing both sides of it by 2,we get(2.4).

(iv)⇒(ii).The method is similar to(v)⇒(iii).

(iii)⇒(vi).Replacing a by 2 and 3 in(2.3),respectively,we have(2.1)and(2.2).Replacing(x,y)by(x+y,2z),(y+z,2x)and(z+x,2y)in(2.1),respectively,we get

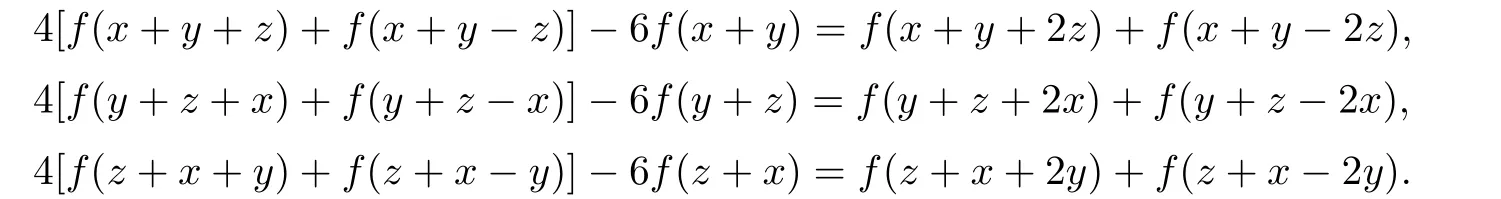
Replacing(x,y)by(x,y+z),(y,z+x)and(z,x+y)in(2.1),respectively,we get

Last,putting(x,y)=(x+y,3z)in(2.2),(x,y)=(z,x+y+z),(x,y)=(x+y-z,2z) in(2.1),respectively,we obtain

Hence we get

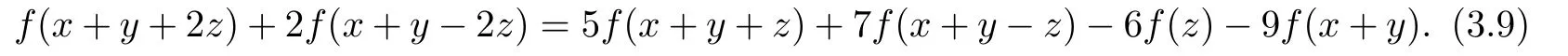
Replacing(x,y,z)by(y,z,x)and(z,x,y)in(3.9),respectively,we get

Then we get(2.6).

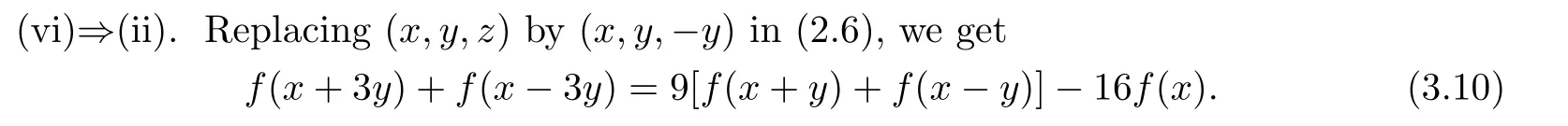
Replacing x by 3x in(3.10),we get

By the property of f:f(ax)=a3f(x),we have

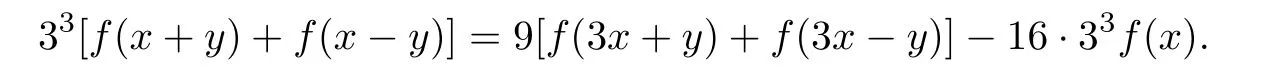
Dividing both sides of above functional equation to 9,we get(2.2).

The proof of the theorem is completed.

Theorem 3.3[8]Suppose that(Ω,d)is a generalized complete metric space,and T:Ω→Ω is a strictly contractive mapping with a constant L.Then for all x∈Ω,one of the following propositions is correct:

(1)For any n≥0,d(Tnx,Tn+1x)=∞;

(2)There exists an n0∈N such that d(Tnx,Tn+1x)＜∞,n≥n0,and

(a)the series{Tnx}is convergent to a fixed point y*of T;

(b)y*is a unique fixed point of T in the set Δ={y∈Ω:d(Tn0,x)＜∞};

By Theorem 3.3,we get the following Theorem 3.4.For convenience,we use the following abbreviation:

Suppose that the function φ:X×X→(0,+∞)satisfies

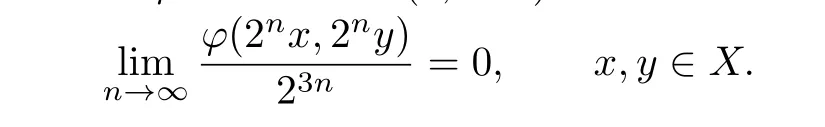
Theorem 3.4Suppose that a mapping f:X→Y satisfies f(0)=0,and

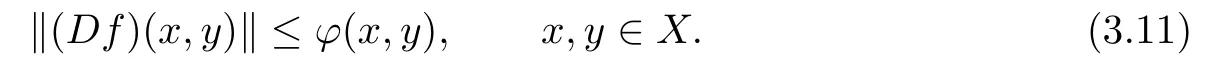
If there exists a constant L with 0≤L＜1 such that the mapping

satisfies

then there exists a unique cubic mapping V:X→Y which satisfies the inequality

Proof.Consider the generalized metric

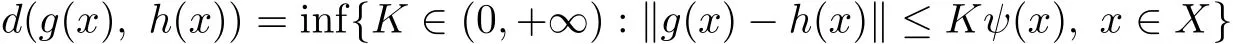
in the space Ω={g:X→Y|g(0)=0}.

Suppose that{gn(x)}∈Ω is a Cauchy series.By definition,for any ε＞0,there exists an N＞0 such that for any m,n＞N we have

Hence,we get the inequality

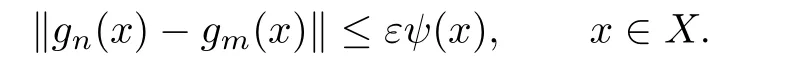
By the arbitrariness of the constant ε and that{gn(x)}is a Cauchy series,we know that Y is complete and{gn(x)}is convergent.Therefore,we define l:X→Y by

Since

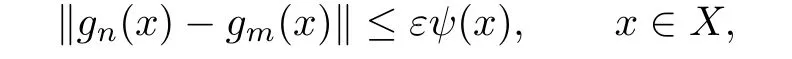
one has

So{gn(x)}has a limit in Ω.Hence the generalized metric spaces(Ω,d)is complete.Define a map T:Ω→Ω by

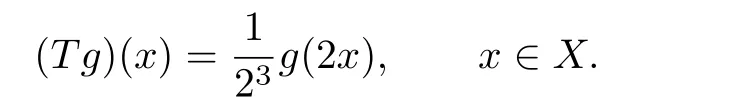
For any g(x),h(x)∈Ω,we have

Henc e

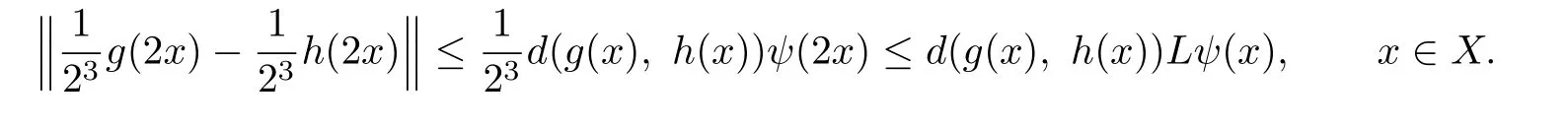
So we obtain

Therefore,T is a strictly contractive mapping with a constant L.Setting y=0 in(3.11), we have

Combining this to(3.12),for any x∈X,we get the inequalities

So we get the conclusion:

By(3.13),for any integer n≥0,we have

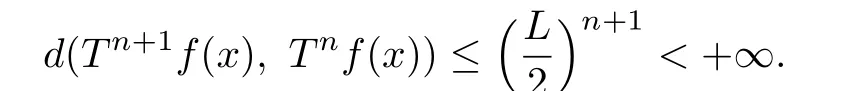
By Theorem 3.3,there exists a fixed point V of the operator T in Ω such that

Therefore,for any ε＞0,there exists an N＞0 such that when n≥N we have

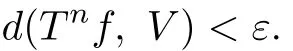
Hence one has

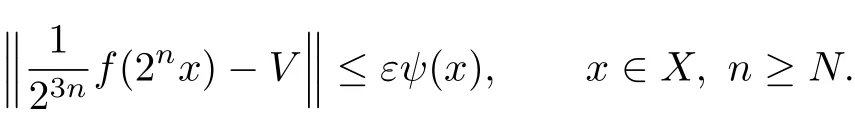
Therefore

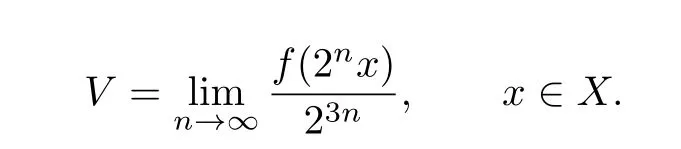
Putting x=2nx,y=2ny in(3.11),and dividing the both sides by constant 23n,we get

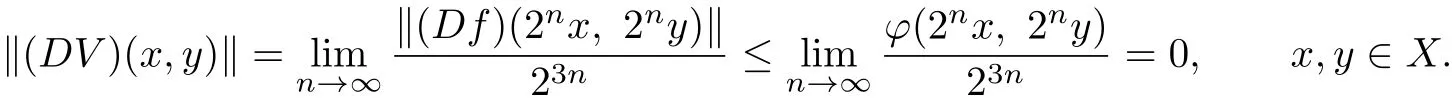
Hence V:X→Y is a cubic mapping.By Theorem 3.3,we have

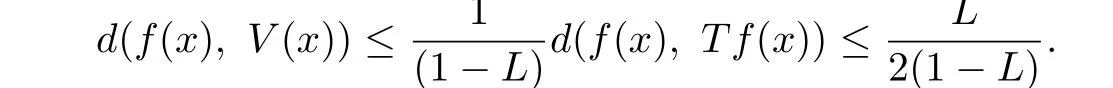
It remains to show the uniqueness of the function V.Suppose that there exists another cubic mapping V1:X→Y which satisfies the condition of the theorem.As

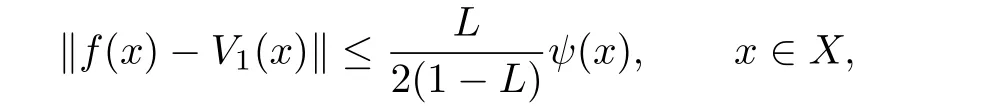
it is easy to get

and

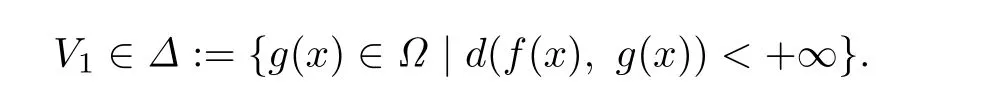
By Theorem 3.3,V is the only fixed point of T in the set Δ,which gives the conclusion

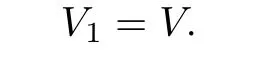
[1]Ulam S M.A Collection of Mathematical Problems.New York:Interscience,1960.

[2]Hyers D H.On the stability of the linear functional equation.Proc.Nat.Acad.Sci.,1941,27: 222–224.

[3]Rassias T M.On the stability of the linear mapping in Banach spaces.Proc.Amer.Math. Soc.,1978,72:297–300.

[4]Badora R.On approximate ring homomorphisms.J.Math.Anal.Appl.,2002,276:589–597.

[5]Gajda Z.On stability of additive mappings.Int.J.Math.Math.Sci.,1991,14(3):431–434.

[6]Hyers D H,Isac G,Rassias Th M.Stability of Functional Equations in Several Variables. Boston:Birkhauser,1998.

[7]Rassias T M.On a modif i ed Hyers-Ulam sequence.J.Math.Anal.Appl.,1991,158:106–113.

[8]Rassias T M,Semrl P.On the Hyers-Ulam stability of linear mappings.J.Math.Anal.Appl., 1993,173:325–338.

[9]Gavruta P.A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings.J.Math.Anal.Appl.,1994,184:431–436.

[10]Isac D H,Isac G,Rassias T M.On the asymptoticity aspect of Hyers-Ulam stability of mappings.Proc.Amer.Math.Soc.,1998,126:425–430.

[11]Park C G.On the stability of the linear mapping in Banach modules.J.Math.Anal.Appl., 2002,275:711–720.

[12]Rassias J M.The Ulam stability problem in approximation of approximately quadratic mappings by quadratic mappings.J.Ineq.Pure Appl.Math.,2004,5(3):article 52,1–20.

[13]Rassias J M.Asymptotic behavior of mixed type functional equations.Aust.J.Math.Anal. Appl.,2004,1(1):article 10,1–21.

[14]Jun K,Kim H.The generalized Hyers-Ulam-Rassias stability of a cubic functional equation. J.Math.Anal.Appl.,2002,274:267–278.

[15]Park K H,Jung Y S.Stability of a cubic functional equation on groups.Bull.Korean Math. Soc.,2004,41:347–357.

[16]Najati A.Hyers-Ulam-Rassias stability of a cubic functional equation.Bull.Korean Math. Soc.,2007,44:825–840.

[17]Najati A,Moradlou F.Stability of an Euler-Lagrange type cubic functional equation.Turk.J. Math.,2009,33:65–73.

[18]Jun K,Kim H,Chang I.On the Hyers-Ulam stability of an Euler-Lagrange type cubic functional equation.J.Comput.Anal.Appl.,2005,7:21–33.

39B52

A

1674-5647(2013)04-0289-08

The NSF(11101323)of China and the SRP(12JK0879)of Shaanxi Education Office.