高职工科专业数学教学中几个典型案例的探讨*

高建云

（天津职业大学基础课部 天津 300410)

高职工科专业数学教学中几个典型案例的探讨*

高建云

（天津职业大学基础课部 天津 300410)

本着加强高等数学知识和应用的联系，针对高职工科专业高中生源的班级设计了几个典型案例：sinθ≈θ与第一重要极限，无理数e与第二重要极限，误差传递与微分，交流电的有效值与定积分。这些案例均从实际应用出发逐步过渡到知识的讲授，期望有助于学生学习动机的激发和知识迁移能力的提高。

高职；工科专业；数学教学；典型案例

案例教学的必要性

当今社会经济的迅速发展，要求劳动者具备很强的适应能力，能够迅速地迁移所学的知识于新的环境中，能够迅速地更新知识以适应新生行业或职业的要求。在此背景下，职业教育更加关注学生素质的全面培养，终身教育思想已成为职业教育的核心。高等数学作为学生整体素质培养的一个重要载体，作为学生理解专业概念和相关理论及计算的重要工具，在学生的整体培养中起着非常重要的基础性作用。

在学生的认知中，不知高等数学有何用，只是听说高等数学有用，或者只是因为开了高等数学课程必须学。在这种认知状况下，学生很难做到积极主动的去学习高等数学，学习效率很低。对于数学的学习与应用的关系，数学家C.雷波特（Report，Cambridge）指出：在某种意义上，把数学的思考方式传递给我们智力工作的其余部分，就是数学的一个应用。当代著名数学家、教育家、沃尔夫奖获得者H.惠特尼（Whitney，Hasselr）指出：“学数学意味着什么？当然是希望能用它……最好的学习就是用，并且古今皆知仅在你有自己的想法时才有真正的学习。”因此，在实际数学教学中适当运用与实际应用有关的教学案例，往往会获得较好的教学效果。如通过微积分的学习，学生不仅可以直接体会到数学是确切表达科学思想的语言，而且可以了解到数学可以为许多重要科学问题提供答案。

高职工科专业高中生源班级的典型教学案例

教学案例是架起数学和应用之间的桥梁，是密切联系数学与应用它的各学科的纽带。适合学生实际情况的教学案例，既可以培养学生应用数学的意识，提高数学应用和知识迁移的能力，也可以调动学生学习的积极性，提高学习效率。下面列举几个可以在高职工科专业高中生源班级中使用的教学案例，这些案例可以让学生体会到高等数学与其他学科的渊源，体会数学的基础性和广泛应用性。

（一）小角度时，sinθ≈θ与第一重要极限

当角度很小时，sinθ≈θ是在工程计算中经常采用的一个近似公式。角度很小是条件，结论是sinθ≈θ，用极限的观点来说就是当θ→0，sinθ→θ，稍加变换为，把θ变为数学上更一般的自变量x就是数学上的第一重要极限，可见，第一重要极限就是其理论依据。由上述的分析可知，在课堂上可以从工程计算中常用到的近似公式sinθ≈θ引入第一重要极限的教学。学生肯定特想知道为什么，此时用单位圆简单地证明一下。

如图1所示，在单位圆中取∠AOB=x（弧度），，AC为切线，BD为△OAB的高。

由图容易得知S△OAB＜S扇形OAB＜S△OAC，即：

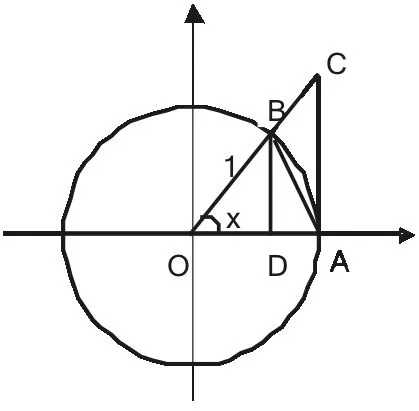
图1 第一重要极限证明示意图

从函数的变化趋势上分析，当x从零的右侧趋近于零时，cosx的极限是1，常数1的极限也是1，所以的极限也应该为1。当x从零的左侧趋近于零时，可令的极限为1，即。

综上所述，当x趋向于零时，。

（二）无理数e与第二重要极限

e和π是常用的两个无理数，与圆周率π易于理解不同的是，e常令人难以理解。e是一个奇妙的无理数，其值是2.71828……，在科学技术中一般不使用以10为底数的对数，而代之以e为底便可使许多式子都能得到简化，用它是最“自然”的，所以叫“自然对数”，在人口增长、细菌繁殖、放射物衰变、冷却定律、电路电流等很多场合都会出现e的身影。

e在微积分中常常出现，但它的诞生比微积分还要早上几百年，它的出现很可能和计算利息有关。我们都知道复利计息的计息周期越短，本利和就越高。若计息周期无限制地缩短，比如说每分钟计息一次，甚至每秒或者每一瞬间（理论上来说），会发生什么状况，本利和会无限制地加大吗？答案是不会，它的值会稳定下来，趋近于一极限值，这一极限值就是e。因为当时还没有极限的概念，所以，e的值很可能是观察出来的。而复利计息的计息周期无限缩短，本利和的计算本就可以用数学的极限表示为所以我们可以用下面的案例引入第二重要极限的教学，用归纳和观察得到第二重要极限。

例如，某顾客在银行存入本金p元，n年后他在银行的存款额是本金及利息之和。设银行规定年复利率为r，试根据下述不同的结算方式计算顾客n年后的最终存款额。

（1）每年结算一次；

（4）当m趋于无穷时，结算周期变为无穷小，这意味着银行连续不断地向顾客付利息，这种存款方式称为连续复利。试计算连续复利情况下顾客的最终存款额。

教师可用递进的形式通过学生讨论、归纳、适当提示的方式得到连续复利的极限表达式，然后通过观察m取不同值时此函数的变化趋势，画出草图，从图上升华得到第二重要极限和自然常数e。

（三）误差传递与微分

在实际实验和测量中，对精密度较高且较易测量的量采用直接测的方法，对不易直接测量的量采用间接测的方法，即利用已知的函数关系通过对直接测量量的计算得到间接测量量。由直接测量量的误差导致的间接测量量的误差就是误差传递。用数学的语言去分析可以这样说：把直接测量量作为自变量，间接测量量作为函数，直接测量量的误差可理解为自变量的微小改变，间接测量量的误差认为是由自变量的微小改变导致的函数的改变量，这正是微分的含义。

为了使上述分析更易理解，可用下面的具体问题来引入微分教学：在生产实际中往往需要了解圆柱体的横截面积，而横截面积不易直接测量，直径较易测量，我们已测得一根圆柱的直径为43cm，并已知仪器的最大绝对误差为0.2cm，那么，该圆柱横截面积的绝对误差与相对误差分别为多少?

（四）交流电的有效值与定积分

在电机、电器上常会标有功率、电流、电压的数字.如电机上标有xxKW，xxxV，在灯泡上标有xxW、220V等，这些数字表明交流电在单位时间内所做的功和交流电压。但交流电流、电压的大小和方向都随时间作周期性的变化，怎样确定交流电的功率、电流、电压呢？

由于交流电随时间做周期变化，电器上标注的功率是一个周期内的平均值。交流电虽然在不断变化，但在很短的时间间隔内，可以近似地认为是不变的（即近似地看作是直流电），

因而在dt时间内对“i=i（t）”以常代变，可得到功的微元：

在一个周期的时间内吸收（消耗）的电能W可以用定积分表示为：

我国的生产生活用电的频率是50Hz，周期为0.02s，所以1s内电压的平均值为零，所以工程师标注

结语

本文针对高职工科专业高中生源的班级设计了几个教学案例，体现了如何从应用到数学知识的过渡，可以在课堂上使用。由于高等数学教师多为数学专业出身，对于应用数学的学科背景不是很熟悉，微积分课程也多在大学一年级开设，学生的专业知识也不多，若案例涉及过多的专业背景会冲淡学生对数学基本概念和基本方法的掌握，所以，我认为案例按专业大类划分即可，不必细分到学生所在的每一个专业。

[1]李新灿.高等数学应用205例[M].北京：高等教育出版社，2003.

[2]张立圃，杜俊文.应用数学[M].北京：机械工业出版社，2011.

[3]赵绪福，李美琴.案例教学法在工科专业数学教学中的应用探讨[J].湖南师范大学教育科学学报，2006，5（4).

[4]胡振媛.高职数学案例教学探究[D].济南：山东师范大学，2007.

[5]胡秀平，甄晨光.高职数学案例教学法的教学实效性刍议[J].科教文汇，2010（6下).

[6]钱志良.论案例教学在《高等数学》教学中的重要性与可行性[J].常州信息职业技术学院学报，2010，9（2).

[7]王新力.高等数学能力本位课程改革实践[J].职业技术教育，2010，31（35).

G712

A

1672-5727（2013）06-0116-02

高建云（1979—)，女，河北阜城人，硕士，天津职业大学基础课部讲师，研究方向为高职数学和物理教学改革。

天津市高等教育学会“十二五”教育科学规划课题《网络化共享型高职校本教学资源库建设的研究与实践——以高职数学校本教学资源库为例》（项目编号：125y112)；天津职业大学“十二五”教育教学改革研究项目《高职数学教学案例的开发》