一种K-分布杂波参数估计方法
2013-08-10陈永森
徐 伟,陈永森
(船舶重工集团公司723所,扬州225001)
0 引 言
在K-分布杂波背景中进行恒虚警处理或者信号检测时,需要准确估计其分布参数,较大的估计误差会导致较高的虚警概率。国内外学者对K-分布的参数估计进行了大量的研究,目前最有效的参数估计方法是最大似然法。由于K-分布的解析形式相对复杂,最大似然估计的解析式很难获得,其参数估计需要用数值方法在二维参数平面内进行搜索[1],计算量较大。此外,基于最大期望值(EM)的方法[2]以及基于神经网络估计的方法[3]需要多次迭代,实现复杂,收敛时间较长,因此工程上大都采用运算相对简单的矩量法[4-5]。这种方法受噪声和数据长度的影响较大,个别样本甚至无法得出计算结果。Blacknell将矩量法进行了推广[6],即利用xln(x)的各阶期望进行参数估计,但仍然无法满足实际杂波处理要求。本文针对该问题,从工程应用角度出发,提出利用ln(x)的一、二阶矩求解K-分布杂波的形状参数和尺度参数的方法,这种方法受噪声影响较小,能够有效避免错误估计的发生,仿真和实测杂波数据处理表明了该方法的准确性和有效性。
1 参数估计
K-分布的概率密度函数为[4]:

式中:Γ(·)为伽马函数;Kv-1为v阶第二类修正贝塞尔函数;a为尺度因子,a>0;v为形状参数,v>0,v越大,f(x)越向右偏离,x>0。
K-分布的r阶矩[4]为:

文献[4]提出利用K-分布的各阶矩估计其参数的方法,即:
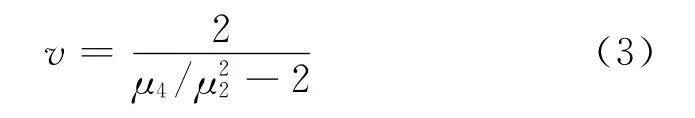
由式(2)得:

实际杂波处理中,当杂波的形状参数v较大时,由式(4)知,f(v)≈2。当受到噪声和有限数据长度的影响时,通过数值方法获得的二、四阶矩存在误差,个别样本出现的情况,此时利用式(3)进行估计,会得出的错误估计结果。文献[6]提出的基于xln(x)的方法亦是如此。针对该问题,本文提出利用xln(x)的一、二阶矩估计K-分布参数估计方法,避免错误估计的发生,提高估计精度。
令z=ln(x),由式(1)得z的一阶原点矩为:
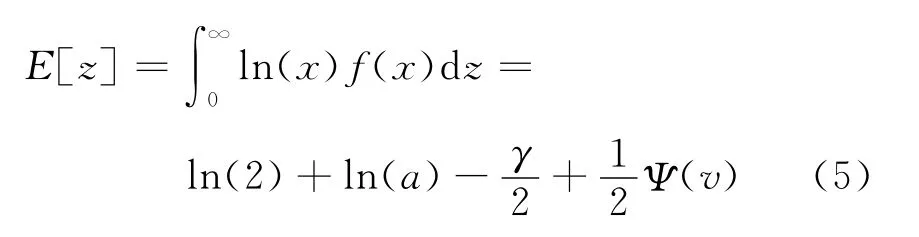
式中:γ为常数;Ψ(·)为Psi函数。
z的二阶原点矩:

由于ln(2a)=ln(2)+ln(a),故可得:

式中:Ψ(1,·)为一阶Psi函数。
式(7)即为形状参数的估计表达式,利用数值方法获得z的一、二阶原点矩求解式(7)即可得到估计值)的值可以通过查表获得。由式(4),得尺度参数a的估计值:
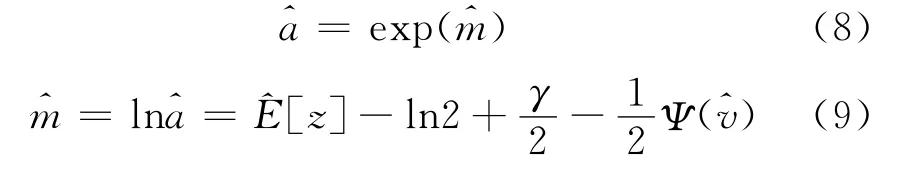
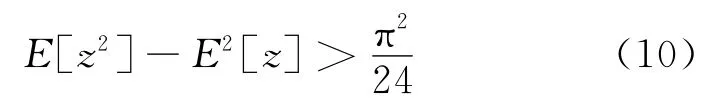
当通过数值方法获得的z的一、二阶矩存在误差时,该方法在E[z]和E[z2]之间提供了余量,保证估计式(7)有解,减少了错误估计的出现。
2 有效性与精度分析
由于K-分布的形状参数v>0,设估计结果0的为有效估计,定义估计有效率ρ为有效估计次数与总估计次数之比。为验证本文方法的估计有效率和估计精度,进行了仿真分析,利用计算机生成不同形状参数的K-分布数据,数据样本点数512个,采用本文方法、常规矩估计方法和xln(x)方法分别进行参数估计,对每个形状进行1 000次仿真,3种方法的估计有效率ρ随形状参数的变化关系如图1所示。
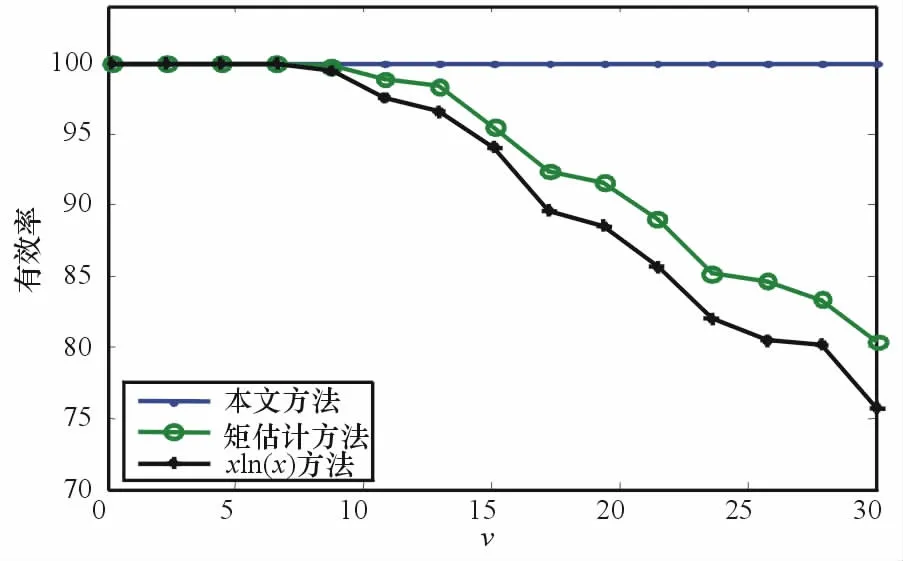
图1 估计有效率
可以看出,当v较小时,3种方法均能以较高的ρ进行估计,但随着v的增大,矩估计方法和xln(x)法的估计有效率逐渐减小,这与分析一致,而本文方法不受此影响。图2给出了3种方法的估计精度,估计精度通过相对误差表征,可以看出3种方法估计精度受形状参数v的影响较大,当v<15时,xln(x)法具有较高的估计精度,本文方法的相对估计误差较大,但在30%以内,能够满足工程要求;当v>15时,本文方法或矩估计方法给出最小的估计误差。

图2 估计相对误差
3 实测数据分析
为验证本文方法的有效性,对169组不同距离单元的实测海杂波数据进行了分析。数据采集条件为:雷达距海面7m,H 极化,脉宽0.5μs,重频5kHz,2级海情。图3所示为第60距离单元的杂波幅度波形和功率谱密度,幅度分布直方图如图4所示,其分布特性偏右,形状参数v较大。
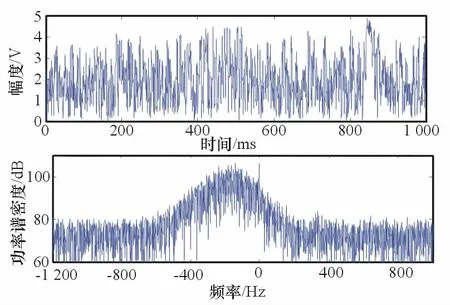
图3 实测杂波数据时域频率波形

图4 杂波幅度分布特性
采用不同方法对该组数据进行参数估计,结果列于表1中。可以看出,矩估计方法和xln(x)法对形状参数的估计结果为负,为错误估计。而本文方法能够给出了v和a的估计结果,按照该估计参数对数据进行K-分布拟合,结果如图4所示。可以看出,拟合结果能够很好地和实测数据相吻合。
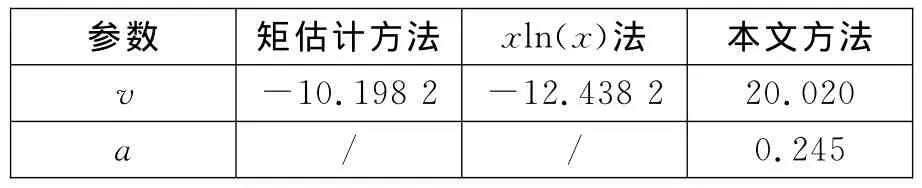
表1 杂波数据参数估计结果
对全部数据进行分析,统计有效估计次数和平均拟合误差,拟合误差的计算方法为:
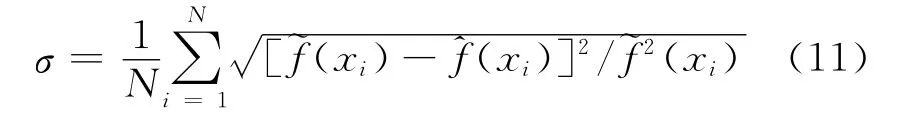
统计结果如表2所示。
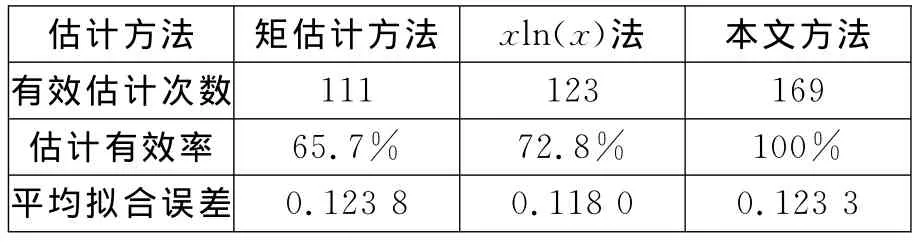
表2 数据处理结果
可以看出,矩估计方法和xln(x)法无法对全部数据进行有效估计,矩估计方法的估计有效率为65.7%,xln(x)法的估计有效率为72.8%;而本文方法对所有数据进行了有效拟合,平均拟合误差介于xln(x)法和矩估计方法之间,能满足工程要求。
4 结束语
本文利用ln(x)的一、二阶矩之间的特定函数关系求解K-分布杂波的形状参数和尺度参数,避免了常规方法在处理杂波数据时由于数据长度有限和噪声所导致的错误估计的发生。利用该方法对不同形状参数的K-分布数据进行了参数估计,结果表明该方法具有很高的估计有效率,利用实测海杂波数据对本文方法进行了处理,说明了本文方法具有很高的工程实用价值。
[1]Joughin I R,Percival D B,Winebrenner D P.Maximum likelihood estimation of K-distribution parameters for SAR data[J].IEEE Transactions on Geosciences and Remote Sensing,1993,31(5):989-999.
[2]Roberts W J J,Furui S.Maximum likelihood estimation of K-distribution parameters via the expectation maximization algorithm[J].IEEE Transactions on Signal Processing,2000,48(12):3303-3306.
[3]Wachowiak M P,Smol kov R,Zurada J M,Elmaghraby A S.Estimation of K distribution parameters using neural networks[J].IEEE Transactions on Biomedical Engineering,2002,49(6):617-620.
[4]Iskander D R,Zoubir A M.Estimation of the parameters of the K-distribution using higher order and fractional moments[J].IEEE Transactions on AES,1999,35(4):1453-1457.
[5]Raghavan R S.A method for estimating parameters of K-distributed clutter.[J].IEEE Transactions on AES,1991,27(2):238-246.
[6]Blacknell D,Tough R J A.Parameter estimation for the K-distribution based on[zlog(z)][J].IEE Proceedings-Radar,Sonar and Navigation,2001,148(6):309-312.
