基于层次分析法的协同干扰资源调度模型

李银钊，倪天权，薛 羽

（1.解放军91404部队，秦皇岛066001；2.船舶重工集团公司723所，扬州225001；3.南京航空航天大学，南京210016）

0 引 言

协同干扰资源调度（CJRS）问题是指在现代战争中面对敌方导弹、飞机所依赖的制导、导航、轰瞄、火控、预警和地形回避等多种雷达，如何合理分配我方干扰机对敌方目标雷达辐射源施放干扰，最大限度地发挥干扰机的整体作战能力。CJRS属于武器－目标分配（WTA）问题。

目前，国内外将WTA问题的研究与人工智能技术研究相结合，使WTA问题的研究进一步深入，例如，Lee分别将多种不同的局域搜索技术引入到遗传算法中以提高遗传算法求解广义武器－目标分配（GWTA）问题的效率［1］。此外，在 GWTA问题求解算法上，一些研究人员还在智能优化算法和传统精确算法相结合方面进行了探索［2］。

目前，在电子对抗研究领域协同干扰方面取得了一些初步的研究成果，例如，文献［3］针对通信网络以组网协同干扰的方式建立了以干扰覆盖最大化为目标的协同干扰最佳覆盖任务分配模型。然而，文献［3］仅考虑了能耗约束，没有考虑干扰样式、工作频段、目标雷达威胁等级等约束限制。此外，文献［3］假设所有干扰机相同，但在实际作战环境中干扰机种类繁多且性能不一。因此，文献［3］中的协同干扰模型和实际问题存在较大的差别。

最近，文献［4］针对多无人作战飞机协同干扰空战决策问题建立了优化模型，并为求解模型提出了一种启发式自适应离散差分进化（H－SDDE）算法，文献［4］在模型建立方面做了初步工作，但其主要工作集中在新型算法的设计、实现和算法性能提升方面。尽管文献［4］在模型建立上有所改进，但文献［4］中的干扰机和雷达模型相对比较简单，且没有给出干扰效能评估指标权重具体计算方法。影响干扰效能的决定性因素很多，应综合考虑影响干扰效能的我方干扰机、敌方目标雷达和战场态势中的各种参数，在此基础上建立更加合理的CJRS问题模型。

本文分别从干扰机和目标雷达数目、干扰功率、干扰样式、目标雷达工作体制、目标雷达和干扰机工作频段、目标雷达威胁等级等11个方面建立干扰效能评估指标体系，并对各项评估指标进行了量化，在此基础上提出了干扰效能多指标综合评估方法。其中，评估结果是否合理与各项评估指标的权重有着直接的关系，运用层次分析法（AHP）能够减少主观确定权重的影响，提高决策质量。因此，本文根据CJRS问题的实际特点给出了各项评估指标的重要程度，并采用AHP方法计算每项评估指标的权重，然后给出了干扰效能多指标综合评估模型，基于此，提出了CJRS问题多约束非线性组合优化模型。

1 干扰效能评估指标量化计算模型

在文献［4］所采用的4个干扰评估指标的基础上扩展了以下7个相关的评估指标：

（1）雷达威胁等级评估（ERTL）计算模型

将雷达威胁分为5个等级，根据经侦察、跟踪、数据关联、数据融合、态势评估后得到的雷达威胁等级计算ERTL的值，威胁等级越高，ERTL值越大。ERTL的计算表达式为：

式中：Lrt为目标雷达的威胁等级。

（2）干扰机抗干扰能力评估（EAJ）计算模型

干扰机抗干扰能力越大，EAJ值越大。本文将干扰机抗干扰能力分为5级，且级别越高抗干扰能力越强。EAJ的计算表达式为：

式中：Laj为干扰机的抗干扰能力等级。

（3）干扰机能耗生存时间性能评估（ELT）计算模型

根据干扰机的能耗生存时间情况计算，若能耗生存时间比预计执行干扰任务时间长，则ELT值为1；否则，能耗生存时间越长，ELT值越大。ELT的计算表达式为：

式中：tjl为干扰机的能耗生存时间；tjn为完成干扰任务预计所需要时间。

（4）干扰机频率瞄准精度评估（ESP）计算模型

根据干扰机的频率瞄准精度是否在允许的范围内计算，若是，则频率瞄准精度越高，ESP值越大；若干扰机的频率瞄准精度不在允许的范围内，则ESP值为0。ESP的计算表达式为：

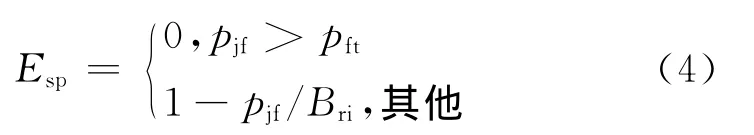
式中：pft为所需频率瞄准精度阀值；pjf为干扰机的频率瞄准精度；Bri为目标雷达的瞬时带宽。

（5）干扰延迟时间评估（EJDT）计算模型

若干扰延迟时间在允许的范围之内，则延迟时间越短，EJDT值越大；否则EJDT值为0。EJDT的计算表达式为：

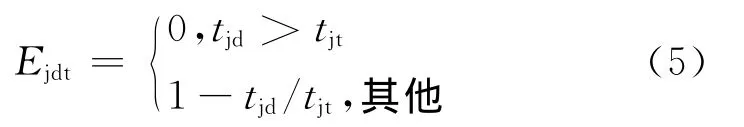
式中：tjd为干扰机的干扰延迟时间；tjt为干扰延迟时间阈值。

（6）干扰机响应时间评估（ERT）计算模型

若干扰机的响应时间在允许的范围内，则响应时间越短，ERT值越大；若响应时间不在允许范围内，则ERT为0。ERT的计算表达式为：

式中：tjr为干扰机的响应时间；trt为响应时间阈值。

（7）干扰机频率转换时间评估（EFST）计算模型

根据干扰机的频率转换时间是否小于目标雷达的频率转换时间计算EFST，若是，则频率转换时间越短，EFST值越大；否则EFST值为0。EFST的计算表达式为：

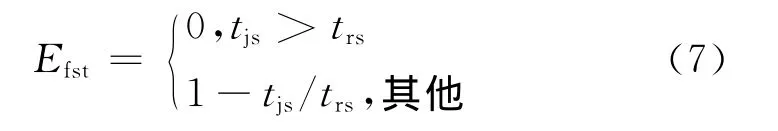
式中：tjs为干扰机的频率转换时间trs为目标雷达的频率转换时间。

2 基于AHP的干扰效能评估指标权重计算方法（AHP－WCMEIJE）

本文采用多评估指标加权平均法计算某部干扰机对某部雷达的干扰效能，然而怎样确定各项评估指标的权重成为难以解决的问题。根据专家经验确定权重的方法虽然简单，但难以克服主观因素的巨大影响，因此，其合理性和可用性不高。本文提出采用AHP方法解决各项评估指标的权重计算问题。AHP是Saaty教授提出的一种定性和定量相结合的、层次 化、系 统 化 的 多 准 则 决 策 分 析 方 法［5－7］。AHP的特点是在对复杂问题的本质、影响因素及其内在关系深入分析的基础上利用较少的定性信息使决策的思维过程数学化、系统化，从而为复杂决策问题提供简便的评价决策方法，AHP适用于对决策结果难以直接准确计量的问题［8－11］。

AHP的关键步骤主要分为3步：

（1）层次构造（一般分为目标层、准则层和属性层）；

（2）构建各层判断矩阵；

（3）计算层次单排序和层次总排序。

为了计算各项干扰效能评估指标的权重，本文根据少量定性信息直接构建判断矩阵并采用层次单排序计算方法计算各项评估指标的权重，主要计算步骤如下：

步骤1，构造判断矩阵

采用向量I＝ （I1，I2，…，I11）表示第二部分中的11项评估指标。根据实际CJRS问题经验知识，将各项评估指标按对干扰效能影响的重要程度分组为：｛I1，I2，I3，I4，I7｝为最重要；｛I5，I9｝为比较重要；｛I6｝为较重要；｛I8｝为一般重要；｛I10，I11｝为相对不重要。采用以上分组信息作为输入，采用5标度法［10］构造判断矩阵，记作：

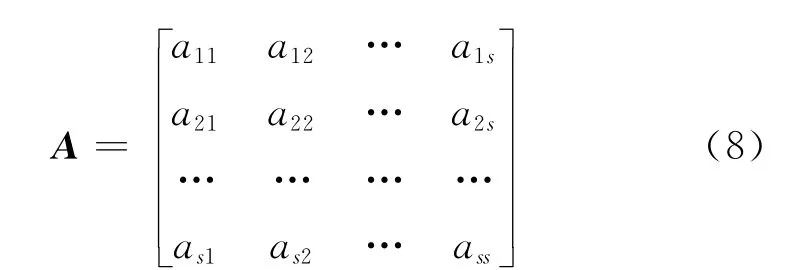
步骤2，评估指标权重计算

对步骤1中的判断矩阵，进行相对权重的计算，计算表达式如下：

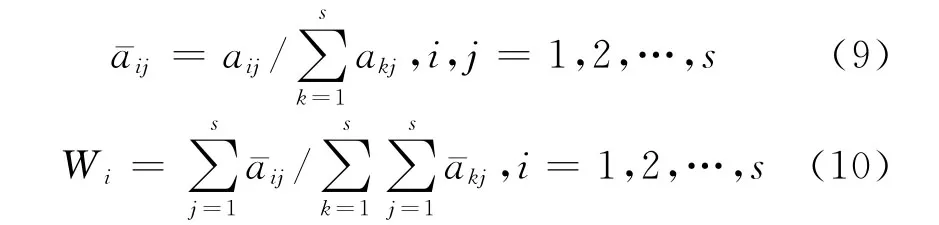
由式（9）、（10），最终可得到评估指标权重向量W＝（W1，W2，…，Ws）。

步骤3，一致性检验

（1）计算判断矩阵的最大特征根：

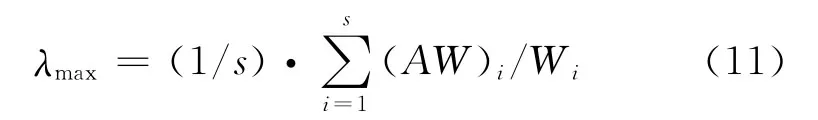
式中：λmax为判断矩阵的最大特征根；W为特征向量；A为判断矩阵；（AW）i为向量AW的第i个元素。

（2）计算一致性指标IC：

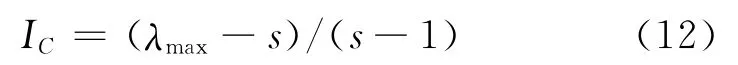
（3）计算一致性比例RC：

式中：IR为平均一致性指标，它是多次重复计算s阶随机判断矩阵的特征根，然后取算术平均值作为平均一致性指标。

当RC＜0.1时，一般认为判断矩阵的一致性是可以接受的。本文采用5标度法，根据评估指标分组情况构造的判断矩阵如下［9，11－14］：

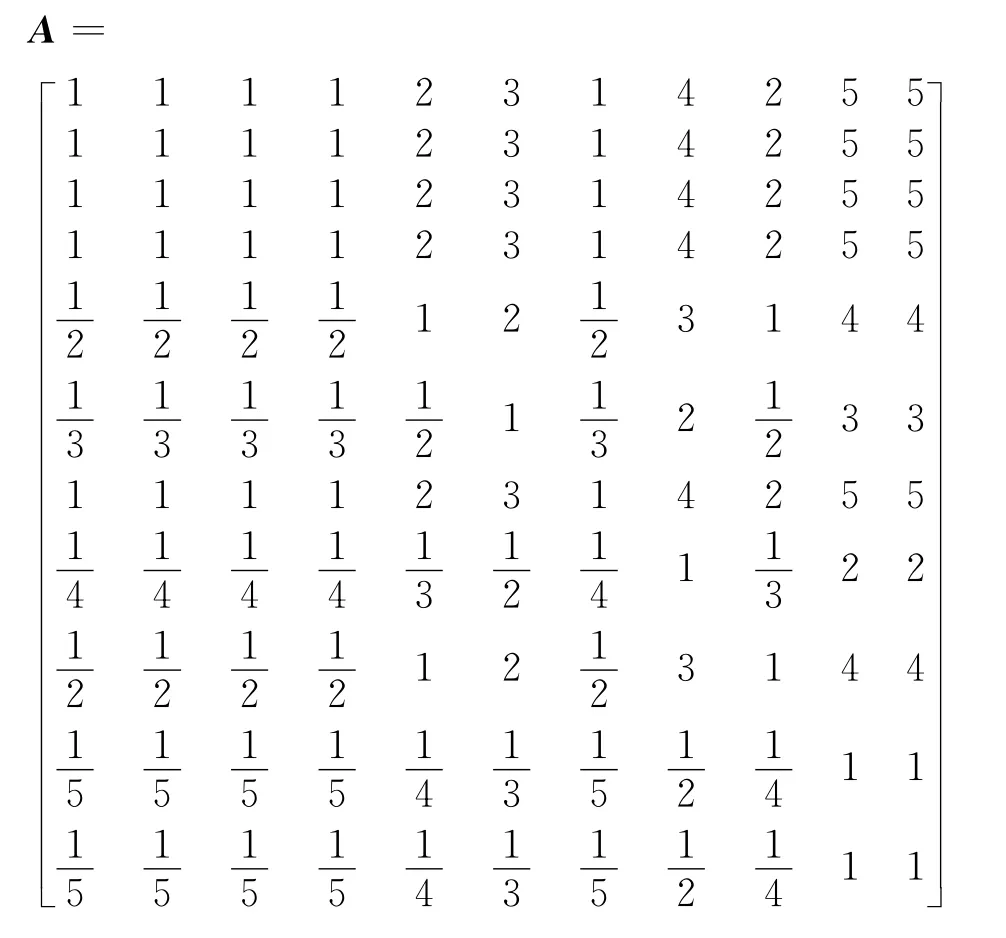
根据以上计算步骤求得的评估指标权重向量为W＝（0.140 1，0.140 1，0.140 1，0.140 1，0.082 0，0.052 5，0.140 1，0.035 1，0.082 0，0.023 9，0.023 9）；最大特征根λmax＝11.126 1；一致性指标IC＝0.012 6。易知，11阶矩阵的IR＝1.52［11－14］，因此，由式（13）可计算出RC＝0.008 2＜0.1，因此，所求结果满足一致性检验，是可以接受的。

3 CJRS问题模型

3.1 干扰效能多指标综合评估模型（MI－JECEM）

设n部干扰机对抗m部雷达，先仅考虑某干扰机Jj（j＝1，2，…，n）对某雷达Ri（i＝1，2，…，m）施放干扰的情况，记Ejr表示Jj对Ri施放干扰获得的干扰效能。Ejr的表达式为：

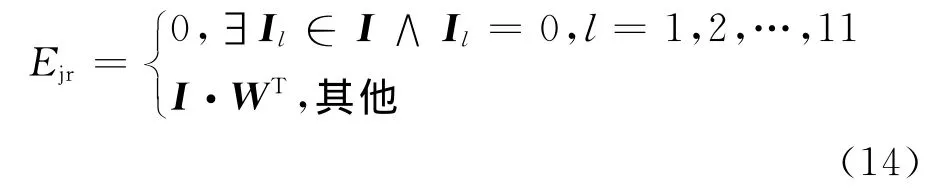
由此可计算出每部干扰机对每部雷达的干扰效能。

3.2 基于MI－JECEM的CJRS问题优化模型

CJRS问题的目标是优化分配方案使协同干扰总体期望效果达到最大［4］。基于干扰效能评估指标量化计算模型、干扰效能评估指标权重计算方法和干扰效能多指标综合评估模型，可以为CJRS问题建立多约束非线性组合优化模型如下：

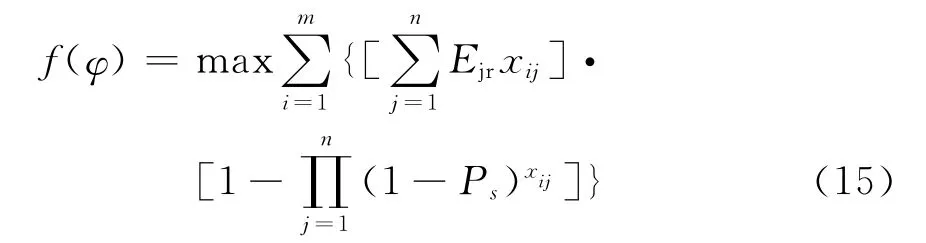
式中：φ表示协同干扰方案，记为φ＝ ［φ（1），φ（2），…，φ（n）］，其中，第j（j＝1，2，…，n）个位置表示第j部干扰机，第j个位置上的数值表示某目标雷达编号；Ps为干扰成功的概率，此变量为经验数据；xij为决策变量。

式（16）表示每个目标雷达至少被分配1部干扰机：

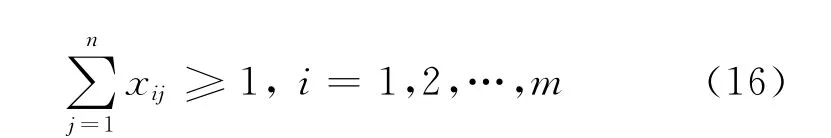
式（17）表示某时刻干扰机只能对一个目标施放干扰：

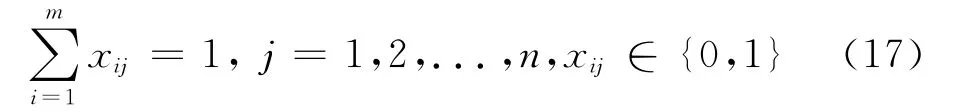
在该模型的基础上可采用不同的优化技术［15－16］进行求解。

4 结束语

本文针对电子对抗领域协同干扰资源调度问题，综合分析了11种干扰机对目标雷达的干扰效能评估指标，并给出了这些指标的量化计算模型，然后采用AHP解决了干扰效能评估指标的权重计算问题，随后建立了干扰效能多指标综合评估模型，在此基础上，结合实际问题中存在的约束条件，建立了CJRS问题多约束非线性组合优化模型。所建立的CJRS问题模型较全面地反映了影响协同干扰资源调度问题的评估指标，评估指标权重计算合理。因此，模型具有较好的可用性。在此模型的基础上，可采用各种离散智能优化技术对其求解。

［1］Lee Z J，Su S F，Lee C Y.Efficiently solving general weapon－target assignment problem by genetic algorithms with greedy eugenics［J］.IEEE Transactions on Systems Man and Cybernetics Part B－Cybernetics，2003，33（1）：113－121.

［2］Ahuja R K，Kumar A，Jha K C，et al.Exact and heuristic algorithms for the weapon－target assignment problem ［J］.Operations Research，2007，55 （6）：1136－1146.

［3］黄郡，单洪，满毅.基于区域覆盖的协同干扰任务分配模型及算法［J］.兵工学报，2011，32（6）：725－732.

［4］薛羽，庄毅，张友益，等.基于启发式自适应离散差分进化算法的多UCAV协同干扰空战决策［J］.航空学报，2012，34（2）：343－351.

［5］Saaty T L.How to make a decision：the analytic hierarchy process［J］.European Journal of Operational Research，1990，48（1）：9－26.

［6］Saaty T L.A scaling method for priorities in hierarchical structures［J］.Journal of Mathematical Psychology，1977，15（3）：234－281.

［7］Saaty T L，Vargas L G.The Seven Pillars of The Analytic Hierarchy Process［M］.Berlin：Springer，2001.

［8］林闯，胡杰，孔祥震.用户体验质量（QoE）的模型与评价方法综述［J］.计算机学报，2012，35（1）：1－15.

［9］刘川意，汪东升.基于HPCC和层次分析法的高性能计算 系 统 评 价 模 型 ［J］.软 件 学 报，2007，18（4）：1039－1046.

［10］Mikhailov L，Tsvetinov P.Evaluation of services using a fuzzy analytic hierarchy process［J］.Applied Soft Computing，2004，5（1）：23－33.

［11］王文彬，孙其博，杨放春.MANET下环境感知的服务可用性量化评估模型［J］.计算机研究与发展，2012，49（3）：558－564.

［12］黄德才，李秉焱.AHP中群决策的几何平均超传递近似法［J］.控制与决策，2012，27（5）：797－800.

［13］李春生，王耀南，陈光辉，等.基于层次分析法的模糊分类 优 选 模 型 ［J］.控 制 与 决 策，2009，24（12）：1881－1884.

［14］吕跃进，程宏涛，覃菊莹.基于判断可信度的层次分析排序方法［J］.控制与决策，2012，27（5）：787－791.

［15］林闯，李寅，万剑雄.计算机网络服务质量优化方法研究综述［J］.计算机学报，2011，34（1）：1－14.

［16］Xue Y，Zhuang Y，Ni T Q，et al.Enhanced self－adaptive evolutionary algorithm for numerical optimization［J］.Journal of Systems Engineering and Electronics，2012，23（6）：921－928.