高频GPS双差残差模型监测强震地表运动

冯 威，黄丁发，李 萌，张 熙，严 丽

西南交通大学测量工程系，成都 610031

1 引 言

随着GPS接收机技术的发展和高频接收机的普及，高频GPS技术在强震领域得到了越来越广泛的研究和应用［1－5］.且与传统地震仪相比，由于不受振幅限制，GPS能够有效监测大幅度的地面震动，其可为地震预警、救援和相关理论研究提供可靠的信息.

为了满足强震地表运动监测的高精度定位和单历元解算的要求，常用精密单点定位（PPP）模式和差分定位模式来实现高精度的位移解算.由于地震影响的范围较大，采用PPP技术进行地震的地表位移解算［6］具有一定的优势.但由于PPP技术对卫星钟差的精度要求很高，而目前还难以实时获取到精密的卫星钟差信息，因此PPP常用于事后的位移解算.差分定位模式虽然还无需精密卫星钟，但在地震监测应用中需在附近选择一个参考站，而选择较远的测站作为参考站时，数据处理过程变得相对复杂.目前广泛使用的单历元数据处理软件有GAMIT／GLOBK软 件 的 TRACK 模 块［7］，BERNESE 软 件的运动学坐标解算模块［8］，GIPSY软件的高精度运动学数据处理模块［9］，以及Geodetics公司研制的商业软件RTD［10］.虽然这些软件能够实现单历元高精度的位移解算，但它们难以同时在实时数据处理以及长基线高精度解算方面满足地震地表实时监测的要求.

本文基于震时地表震动持续时间短的特点，以及短时间内双差残差的强相关性，提出了双差残差预报的GPS位移监测方法，对各双差残差进行建模，再结合预报残差实现短时间尺度内的位移监测.最后本文将通过长约1100km的静态基线数据和El Mayor－Cucapah 7.2级地震时94个测站的数据来验证本文方法的有效性.

2 双差残差建模

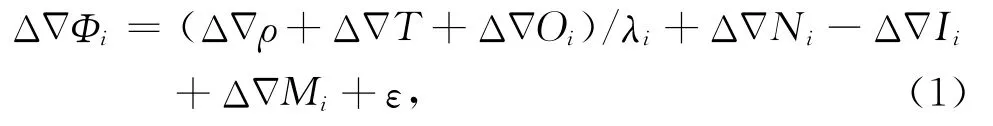
长基线GPS双差观测方程可表达成如下形式：其中Φ为经天线相位中心、对流层模型等改正后的相位观测值，λ为对应的波长，N为整周模糊度，T为对流层残差，I为电离层延迟，O为轨道误差，M为多路径延迟，ε为观测噪声，i（i＝1，2）代表不同频率，ΔΔ代表双差运算.与常用的测站天顶延迟估计加映射函数的模型不同，对流层延迟先通过经验模型改正［11］，再对各卫星的双差对流层残差分别进行建模.

卫星轨道误差所导致的单差测距误差可表示为［12］：

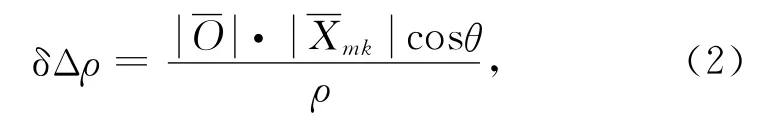
式（1）中，电离层延迟可通过双频消电离层组合消除其影响，而多路径延迟则可通过改进的恒心日滤波的方法来建模［13－14］.经过消电离层和恒心日滤波处理后，式（1）可写成如下形式：

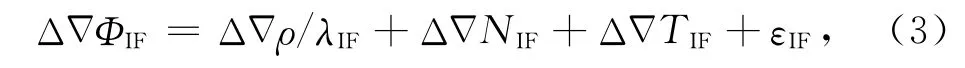
式（3）中的消电离层双差模糊度不再具有整周特性，但是在没有周跳发生的情况下，其是不随时间变化的量.一般情况下，天顶对流层延迟量约为2.4m，可以通过模型有效削除其中90%以上的延迟影响.图1显示了不同卫星高度角下映射函数的值.当高度角高于25°时（图中的虚线处），映射函数值随高度角的变化十分缓慢；当卫星高度角低于20°时，随着高度角的降低，映射函数值急剧增大，因此式（3）中不同卫星高度角的双差对流层残差需采用不同的模型.

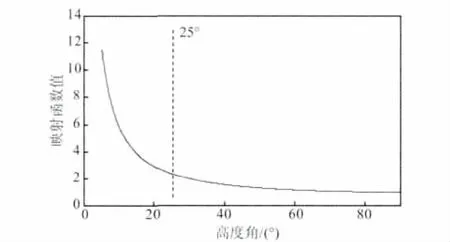
图1 不同卫星高度角的映射函数值Fig.1 The values of mapping function of different elevation

经过双差处理后，对流层残差将得到进一步削弱.对流层残差具有极强的时空相关性，测站天顶延迟变化常是以小时为时间尺度来估计［15］，同时考虑到地震发生时地表震动时间相对较短，卫星高度角变化也较小，由映射函数所引起的误差可近似表达成线性函数.结合图1，双差残差一般可简化成如下模型：

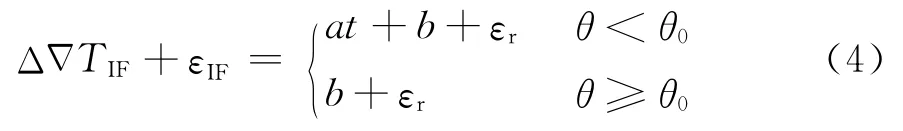
式中t为时间，θ为卫星高度角，θ0为不同模型的分界值，建议值为25°，εr为模型噪声.由于模糊度是一个定值，将模糊度合并到式（4）后有

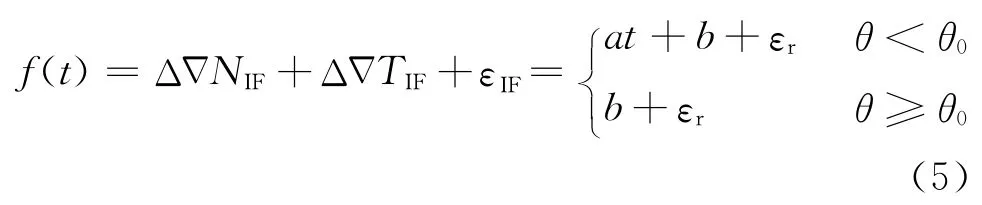
称a和b为双差残差参数，f（t）为双差残差模型.式（3）代入式（5）可得：

地震发生前，测站精确坐标已知，即式（6）中的ΔΔ ρ可视为已知量.通过地震发生前的若干历元，结合最小二乘法即可解算出双差残差参数a、b.

3 基于双差残差预报的地表运动监测

当地震发生时，式（6）中的ΔΔ ρ将会发生变化，可以认为距震中较远（上千公里）的参考站其空间位置保持不动，ΔΔ ρ的变化是由于离震中较近的测站震动而引起.由于天顶延迟通常是以小时为间隔来估计其变化量，而地震地表震动时间短，可忽略其变化量.再结合第2节映射函数相关影响的分析，可以认为地表震动过程中双差残差不发生突变，各双差残差模型f（t）保持不变.图2为4.1节中静态试验部分某两颗卫星的双差残差序列，可以看出在整个过程中双差残差量变化较为平缓.当然在大气变化异常时也可能会出现异常情况，此时可以在建模和定位过程中进行适当的判断，探测是否存在异常.

根据上面分析，式（6）可表达为：

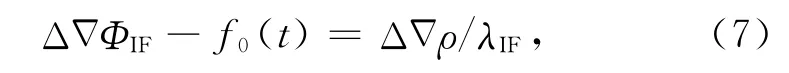
f0（t）为震前所确定的各双差残差模型f（t）的预报值.当一个历元有n颗卫星（参考星除外）可用时，可得如下观测方程：

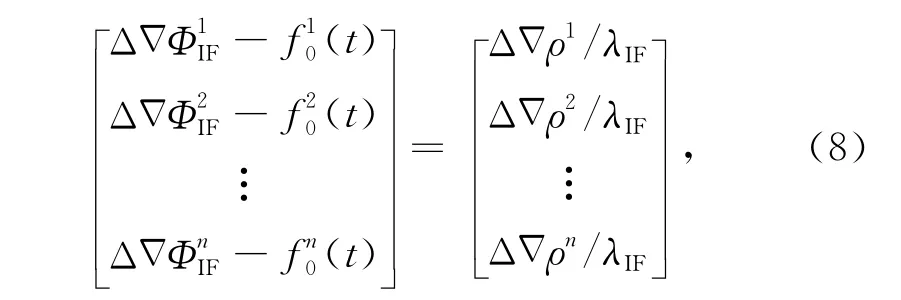
其中上标代表不同的卫星，利用最小二乘法就能解算出震时各个历元的地表位移.

4 试验结果分析

为检验本文方法的有效性，分别采用静态数据和真实地震数据，利用本文方法进行动态定位.试验过程中，采用5min的数据来估计各双差残差模型，并用各模型预报后5min的双差残差，利用预报的双差残差来解算测站的动态位移，解算时采用IGS的预报精密星历.

4.1 静态试验

静态数据采用两个CORS站的观测数据，基线长约1100km，采样间隔为1s，时长为24h，卫星截止高度角设置为5°.以每10min为一个时段进行分段处理，并剔除卫星数少于5的时段.

图3显示了根据预报的双差参数模型解算出的测站动态位移的分布情况，共约解算了38000个历元的位移.统计结果表明，N、E、U三个方向的中误差分别为6mm，6mm，13mm.

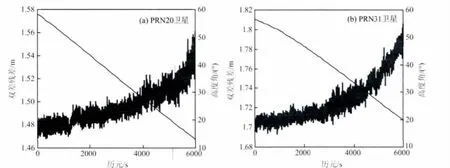
图2 不同卫星双差残差序列图Fig.2 Time series of the double differenced residual value for different satellites

进一步分析双差残差模型，图4显示了两个具有代表性的双差参数的计算值和模型值，其中，双差残差模型是根据前300s的数据解算得出，后300s的模型值为预报值.可以看出，当卫星高度角较低时，双差残差变化显著，设置为常数显然不合理.另外为了防止高次模型因噪声影响而出现震荡现象，应尽量采用低次的模型.因此本文根据不同的卫星高度角分别用一次模型和常数模型来对双差残差建模.

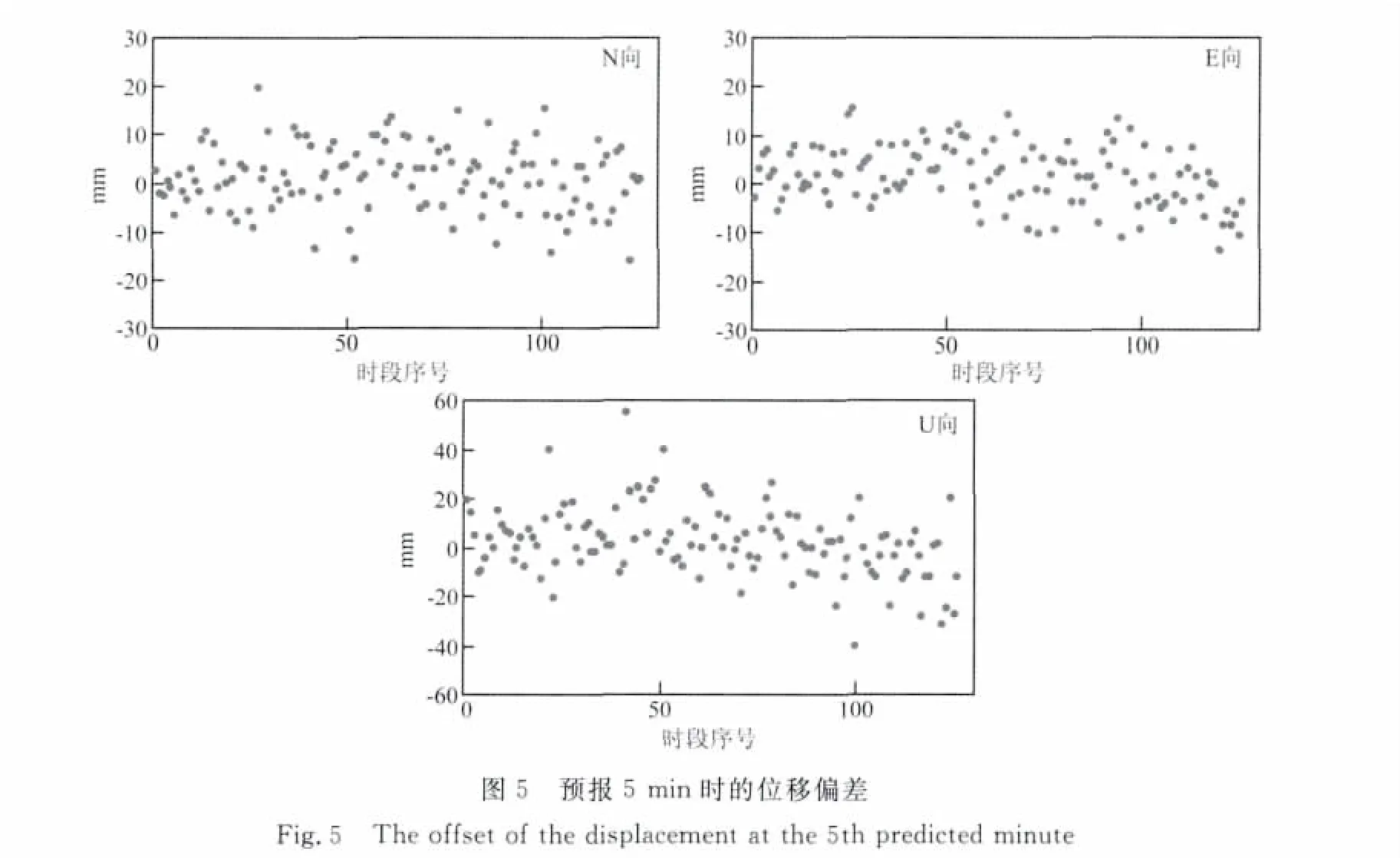
随着预报时间的增加，双差残差的相关性将会减弱.对于一般地震来说，地面震动时候一般不超过5min，因此本文将只分析在残差预报的时间达到5min时，本文方法进行位移监测所能达到的精度.为了削弱随机噪声的影响，将根据最后20个历元的位移信息取平均来计算最终的位移量.本试验共解算了126个时段的数据，结果如图5所示.

可以看出，水平方向的最大值不超过20mm，竖直方向基本不超过40mm.统计结果表明，N、E方向超过92.0%的位移小于10mm，U方向超过91.2%的位移小于20mm.

4.2 El Mayor－Cucapah地震位移解算

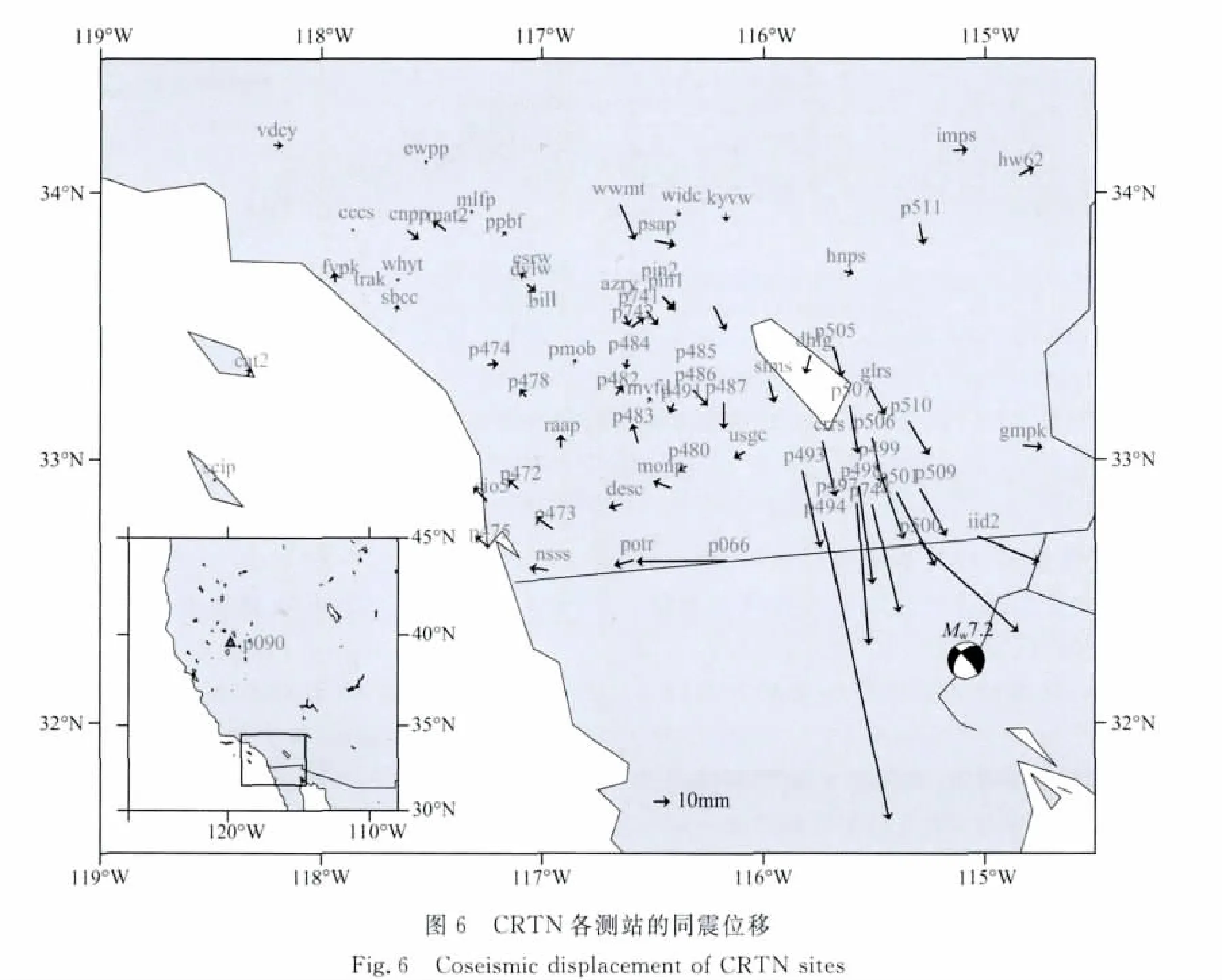
2010年4月4日，在墨西哥Baja地区发生了7.2级强烈地震，主震持续时间超过了40s，地表破裂长度达120km.本文利用加州实时观测网络（CRTN）的1Hz GPS数据［16］，通过本文的方法解算该地震各测站的动态位移和地震同震位移场，参数设置与静态试验相同.

本次试验共解算了94个测站的位移，p090离震中约920km，将其作为参考站.主震之后的部分位移场图如图6所示.

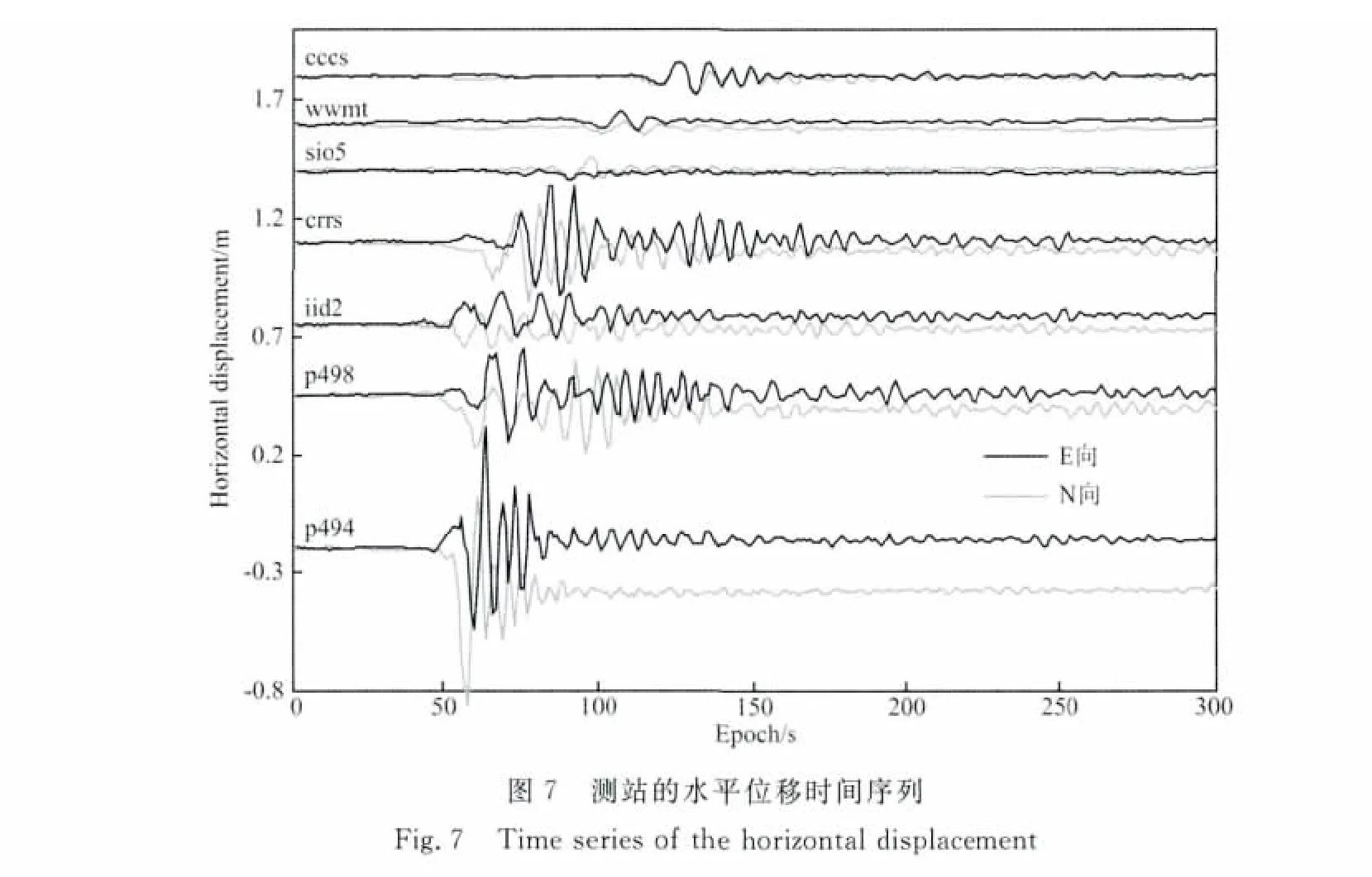
图7画出了其中离震中较近和较远的几个测站水平方向的实时动态位移信息，可以看出，利用本文的方法解算出的GPS时间序列可清楚记录各个测站的地表震动.

为验证解算结果，将本方法解算的同震位移与GPS Explorer提供的高精度后处理结果［16］进行对比，统计了其中66个测站的同震位移的差值，统计结果如图8.可以看出水平方向偏差基本小于20mm，竖直方向偏差基本小于30mm.统计结果表明，与后处理结果相比，N、E方向分别有79%和91%的测站相差小于10mm，U方向有82%的测站相差小于20mm.

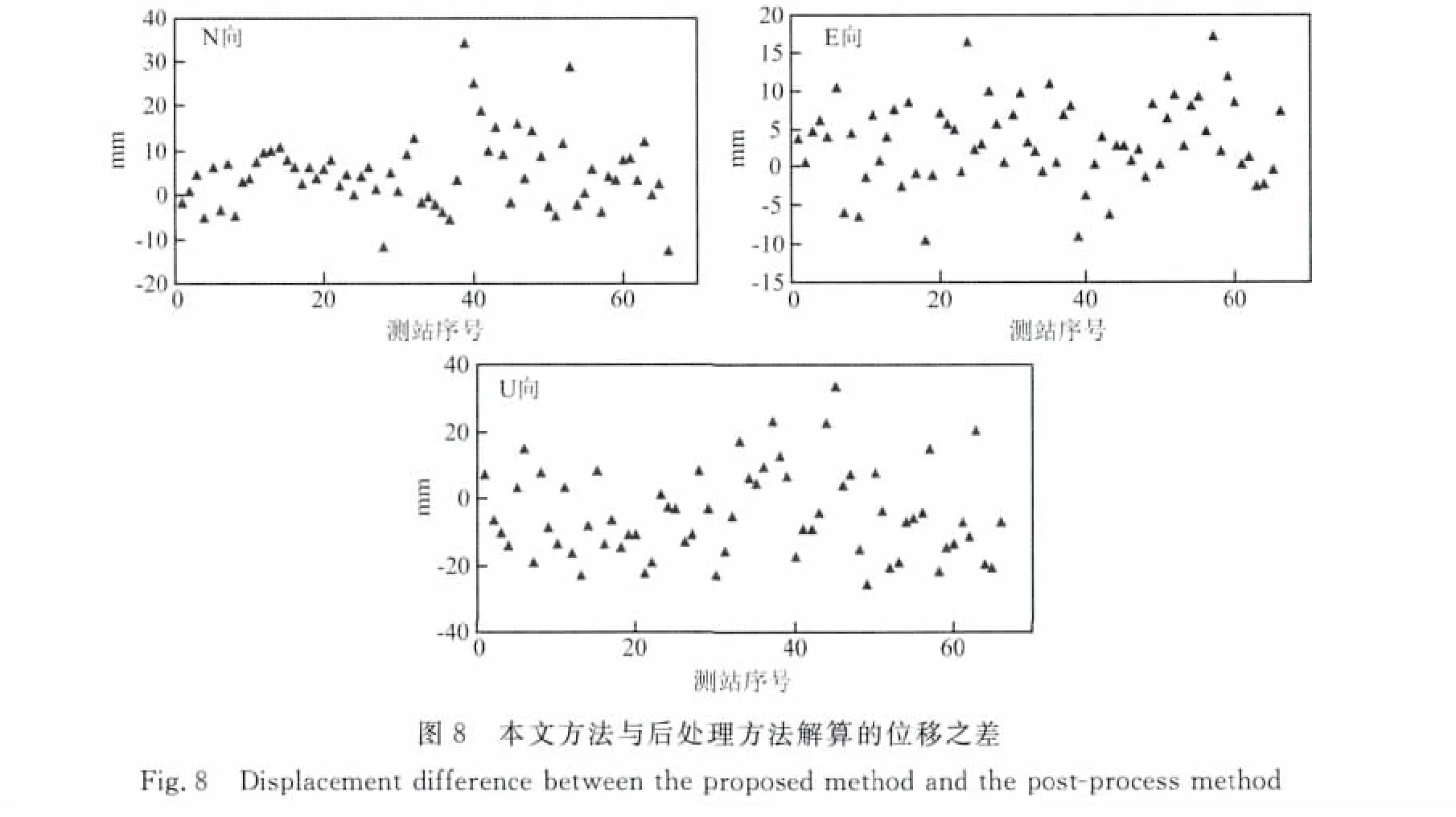
进一步分析N方向差值最大的4个测站，偏差从大到小依次为p494、p744、p497和p498.从图6中可以看出这4个点距震中较近，且位置相对集中.由于事后处理的结果是根据震后几天的数据解算得出，其位移场是震后几天的位移场，而本文解算的是震后几分钟的位移场.两种解算结果在4个测站N、E方向的位移差分别为：－34、－28、－25、－19mm和9、－3、3、0mm.可以看出它们主要呈现出往南偏的趋势，这与同震位移的方向大体保持一致，初步分析两种方法解算结果中较大的差异主要是由于震后滑移所引起.

SOPAC提供的p494和p497两个测站（p744、p498缺少）的快速静态解和本文的解算结果吻合较好，两测站N方向相差约为8mm和14mm，E方向相差约2mm和16mm，进一步证明了该方法的有效性.

5 结 论

根据地震地表震动时间短的特点、以及短时间尺度内双差残差具有极强的相关性，提出了基于双差残差预报的强震地表运动实时监测方法.与传统的基线解算方法不同，该方法不单独解算模糊度信息，而是直接对各双差残差建模，并利用残差模型预报实现上千公里基线的解算.试验结果表明，在5min的预报时间内，1Hz的静态数据该方法N、E、U三个方向的中误差分别为6mm、6mm和13mm，El Mayor－Cucapah地震数据的解算结果也与实际情况有较好的一致性，试验结果证明了本文方法的可行性.本方法只需要预报精密星历，且计算效率高，在有实时观测数据的情况下，可实现强震时测站位移的实时监测，这对地震预警和地震快速救援具有一定的实用和研究价值.

需要注意的是双差参数预报的精度会随着预报时间的增加而降低，本文方法不适用于长时间的地表运动缓慢的监测.本文初步测试了5min预报时间内方法的有效性，对于更长时间的位移监测，方法的有效性尚需进一步研究.此外，周跳对本方法的影响不容忽视，其将影响残差模型和后面的位移解算.

（References）

［1］Shi C，Lou Y D，Zhang H P，et al.Seismic deformation of the Mw8.0Wenchuan earthquake from high－rate GPS observations.Advances in Space Research，2010，46（2）：228－235.

［2］Elósegui P，Davis J L，Oberlander D，et al.Accuracy of high－rate GPS for seismology.Geophys.Res.Lett.，2006，33（11）：L11308，doi：10.1029／2006G1＿026065.

［3］Langbein J，Bock Y.High－rate real－time GPS network at Parkfield： Utility for detecting fault slip and seismic displacements.Geophys.Res.Lett.，2004，31（15）：L15S20，doi：10.1029／2003GL019408.

［4］殷海涛，张培震，甘卫军等.高频GPS测定的汶川Ms8.0级地震震时近场地表变形过程.科学通报，2010，55（26）：2621－2626.Yin H T，Zhang P Z，Gan W J，et al.Near－field surface movement during the Wenchuan Ms8.0earthquake measured by high－rate GPS.Chinese Science Bulletin，2010，55（23）：2529－2634.

［5］Crowell B W，Bock Y，Squibb M B.Demonstration of earthquake early warning using total displacement waveforms from real－time GPS networks.Seismological Research Letters，2009，80（5）：772－782.

［6］方荣新，施闯，徐培亮等.GPS地震仪：PANDA软件测试结果与验证.武汉大学学报 （信息科学版），2011，36（4）：453－456.Fang R X，Shi C，Xu P L，et al.GPS seismometer：PANDA software testing results and validation.Geomatics and Information Science of Wuhan University （in Chinese），2011，36（4）：453－456.

［7］http：／／geoweb.mit.edu／～tah／track＿example／

［8］Bock Y，Nikolaidis R，de Jonge P J，et al.Instantaneous geodetic positioning at medium distances with the global positioning system.J.Geophys.Res.，2000，105（B12）：28233－28253.

［9］Jet Propulsion Laboratory California Institute of Technology.GIPSY5.0Release Note.https：／／gipsy－oasis.jpl.nasa.gov／gipsy／docs／Release＿Nates＿5.0.pdf，2008

［10］http：／／www.geodetics.com／products／software／rtd＿pro.php

［11］Saastamoinen J.Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites，in the use of artificial satellites for geodesy.Geophysics Monograph，1972，15（16）：247－251.

［12］Han S W.Carrier phase－based long－range GPS kinematic positioning［Ph.D.thesis］.Sydney：The University of New South Wales，1997.

［13］Choi K，Bilich A，Larson K M，et al.Modified sidereal filtering： Implication for high－rate GPS positioning.Geophys.Res.Lett.，2004，31：L24610，doi：10.1029／2004GL021621.

［14］Niell A E.Global mapping functions for the atmosphere delay at radio wavelengths.J.Geophys.Res.，1996，101（B2）：3227－3246.

［15］熊永良，黄丁发，丁晓利等.虚拟参考站技术中对流层误差建模方法研究.测绘学报，2006，35（2）：118－121.Xiong Y L，Huang D F，Ding X L，et al.Research on the modeling of tropospheric delay in virtual reference station.Acta Geodaetica et Cartographica Sinica （in Chinese），2006，35（2）：118－121.

［16］http：／／geoapp03.ucsd.edu／gridsphere／gridsphere？cid＝El＋Mayor＋Cucapah