赤道-低纬电离层不规则结构和闪烁活动出现率的理论模型构建
2013-08-09罗伟华徐继生朱正平
罗伟华,徐继生,朱正平
1 中南民族大学电子信息工程学院,武汉 430074
2 武汉大学电子信息学院,武汉 430072
1 引 言
夜间赤道电离层中经常会出现一些不规则的等离子体结构,即电离层不规则结构,或称为赤道扩展F(Equatorial Spread F,简称 ESF),通常表现出显著的随地方时、季节、太阳活动和地理经度的变化以及逐日变化[1].
电离层不规则结构是导致电波闪烁的主要原因.由于散射和衍射效应,无线电波穿过不规则结构传播后,电子密度的随机起伏将导致穿过电离层的电波信号的相位、幅度等产生快速变化,即闪烁.电离层闪烁对远距离的卫星通信和导航系统可产生显著影响.
现在普遍认为,赤道-低纬电离层不规则结构的生成和发展主要归因于广义Rayleigh-Taylor不稳定性(简称R-T不稳定性)[2].要分析影响等离子体不稳定性的物理因素,最直观的就是分析等离子体不稳定性线性增长率.影响R-T不稳定性线性增长率的主要因素包括[2]:背景电离密度梯度;电离层电场(等离子体垂直漂移速度);热层中性风场;碰撞频率;E区电导率等.
Basu[3]特别强调了线性理论分析的重要性:线性理论分析得到的不稳定性增长率可用于预测不规则结构可能出现的时间和区域.
Anderson等[4]首先考虑利用等离子体垂直漂移速度来对不规则结构出现和闪烁活动进行预报.他们指出,等离子体漂移速度与闪烁指数S4之间的对应关系存在一个阈值:当垂直漂移速度大于20m/s时,S4指数通常大于0.5.由于现在所用到的等离子体漂移速度均是经验模式,尽管能较好地描述漂移速度的形态特征,但很难精确描述其逐日变化.因此,仅用等离子体漂移速度来表征不规则结构和闪烁特性还不够,可以考虑利用等离子体不稳定性线性增长率来描述不规则结构和闪烁活动特征.Retterer等[5]将闪烁活动与R-T不稳定性的线性增长率进行了比较,发现线性增长率的大小与闪烁强度之间有较好的对应关系:线性增长率的值越大,闪烁越强.最近,美国提出的以闪烁观测和建立闪烁现报和预报系统为目标的C/NOFS计划建议[6],一个完整的闪烁现报和预报系统应包含观测数据和理论模型两部分.理论模型以等离子体不稳定性的理论分析为主,通过计算线性增长率,预测和估计闪烁可能发生的区域和时间.
Kelley和Retterer[7]根据基于物理模型的闪烁预报系统,利用线性增长率成功预报了一次等离子体耗尽事件.Singh等[8]将通量管积分R-T不稳定性的线性增长率与观测到的甚高频(VHF)闪烁特征比较发现,增长率能反映出闪烁活动的主要特征.罗伟华等[9]将通量管积分R-T不稳定性的线性增长率随地理经度的变化与卫星观测到的等离子体泡出现率随经度的变化进行了比较,发现线性增长率能较好地反映等离子体泡的经度变化特征.
因此,计算分析R-T不稳定性的线性增长率的变化特征,对于了解和研究不规则结构和闪烁活动的形态特征具有指导性的意义,并有助于建立不规则结构和闪烁活动的变化规律的理论模型.
Basu[3]指出,三维分析得到的线性增长率能更为准确地描述R-T不稳定性和不规则结构的线性发展过程.为构建不规则结构和闪烁活动出现率的理论模型,以及为进一步构建电波传播和闪烁模型提供理论基础.本文通过计算分析三维广义R-T不稳定性的线性增长率,研究线性增长率随地方时、季节、太阳活动和地理经度的变化以及逐日变化特征,并将增长率的变化特征与不规则结构和闪烁出现率的变化特征进行比较分析.
2 三维广义R-T不稳定性线性增长率
对电离层中的等离子体不稳定性进行分析,需从描述夜间赤道电离层的守恒方程出发

式中,V为粒子速度,j为电流密度.
在准中性近似下,ne≈ni≈n.假定存在沿磁力线方向的扰动传播.在偶极坐标系 (q,s,l)中,从方程(1)和(2)出发,进行等离子体不稳定性分析,不考虑背景电导率、电场和中性风场的梯度的影响,并忽略扰动沿q方向的传播和背景纵向电场及其梯度的影响,可以得到三维广义R-T不稳定性线性增长率的表达式为[3,10]
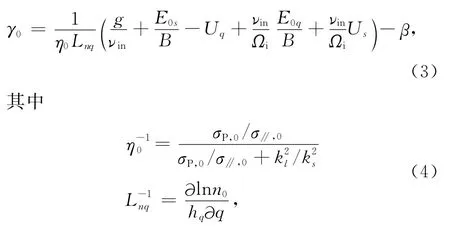
3 线性增长率的形态特征
下面将根据三维条件下分析得到的广义R-T不稳定性的线性增长率的表达式(3),计算不同经度区、不同太阳活动、不同季节和不同地方时的增长率,对增长率进行统计分析,初步建立增长率随地方时、季节、太阳活动和地理经度变化的理论特征模型.计算中所用的电离层模型包括IRI2001[11],HWM07[12]和 MSIS00[13].
3.1 增长率随地方时的变化
图1给出在太阳活动高年(2000年),地理经度为5°E(a,b)和120°E(c,d),线性增长率随地方时的逐日变化.
由图1可以看到,在太阳活动高年,在5°E经度区,在3月和9月期间的2300—2400LT附近,增长率有一个极大值.在午夜之后的0100LT附近,增长率也存在一个极大值.这意味着不规则结构可能在午夜之后出现.在120°E经度区,午夜之前的线性增长率的极大值出现在3月和9月期间的2300—2400LT附近.在午夜之后,3—4月和9—10月的0000LT附近,增长率也存在一个正的极大值,随后,增长率逐渐减小.这意味着不规则结构更易于在午夜前不久出现.
图2给出在太阳活动低年(2005年),地理经度为5°E(a,b)和120°E(c,d),线性增长率随地方时的逐日变化.
由图2可以看到,在太阳活动低年,在5°E经度区,春分期间的增长率极大值出现在2300LT附近,秋分期间的增长率极大值出现在2100LT附近.在午夜之后的0000—0100LT之间,两分点期间的增长率也会有一个极大值,其值可达约0.4×10-3s-1.在120°E经度区,在2000—2200LT期间,增长率的值都较大.线性增长率的极大值出现在3月和9月期间2100LT附近.这意味着不规则结构在这期间更容易出现,闪烁更易发生.在午夜之后,增长率的值大多都为负;在3—4月和9—10月的0000LT附近,增长率也存在一个极大值,但其值非常小.
比较图1和图2可以发现,太阳活动高年期间的增长率明显大于太阳活动低年期间的增长率.在不同太阳活动期间,线性增长率的极大值出现的地方时存在差异.此外,在太阳活动高年期间,在午夜之后,R-T不稳定性的增长率可能为正,这意味着不规则结构可能在午夜之后生成和发展.在太阳活动低年期间,午夜之后的线性增长率都为负或接近于0,这也意味着不规则结构更易于在午夜之前出现,在午夜之后较难生成和发展.
在不同经度区,增长率随地方时的变化特征也存在差异.在太阳活动高年,如图1所示,在5°E经度区,午夜之后的增长率比午夜之前的值要大,极大值出现在0100LT附近.在120°E经度区,增长率的极大出现在午夜之前.在太阳活动低年,如图2所示,增长率的极大值出现的地方时存在差异.在5°E经度区,增长率的极大值主要出现在2100LT和2300LT附近,在120°E经度区,增长率的极大值主要出现在2000—2200LT附近.此外,在5°E经度区,午夜之后的增长率仍可能为正,而在120°E经度区,午夜之后的增长率基本为负.这意味着不规则结构仍可能在某些经度区的午夜之后出现.
3.2 增长率随地理经度的变化
图3给出一个太阳活动周期内(1997—2007年),线性增长率的平均值随地理经度和季节的变化.图4给出太阳活动中年和太阳活动高年期间(1999—2004年),线性增长率的平均值随地理经度和季节的变化.
由图3和图4可以看到,线性增长率的平均值表现出显著的随地理经度和季节的变化.在300°E—360°E经度区,线性增长率在3—4月和9—10月有极大值.在0°E—30°E经度区,线性增长率在3—4月和9—10月也存在极大值,其值较300°E—345°E经度区的值要小.在45°E—90°E经度区和255°E—330°E经度区的6—8月期间,线性增长率有极小值.相比其它地理经度区的值,30°E—210°E经度区的线性增长率较小.
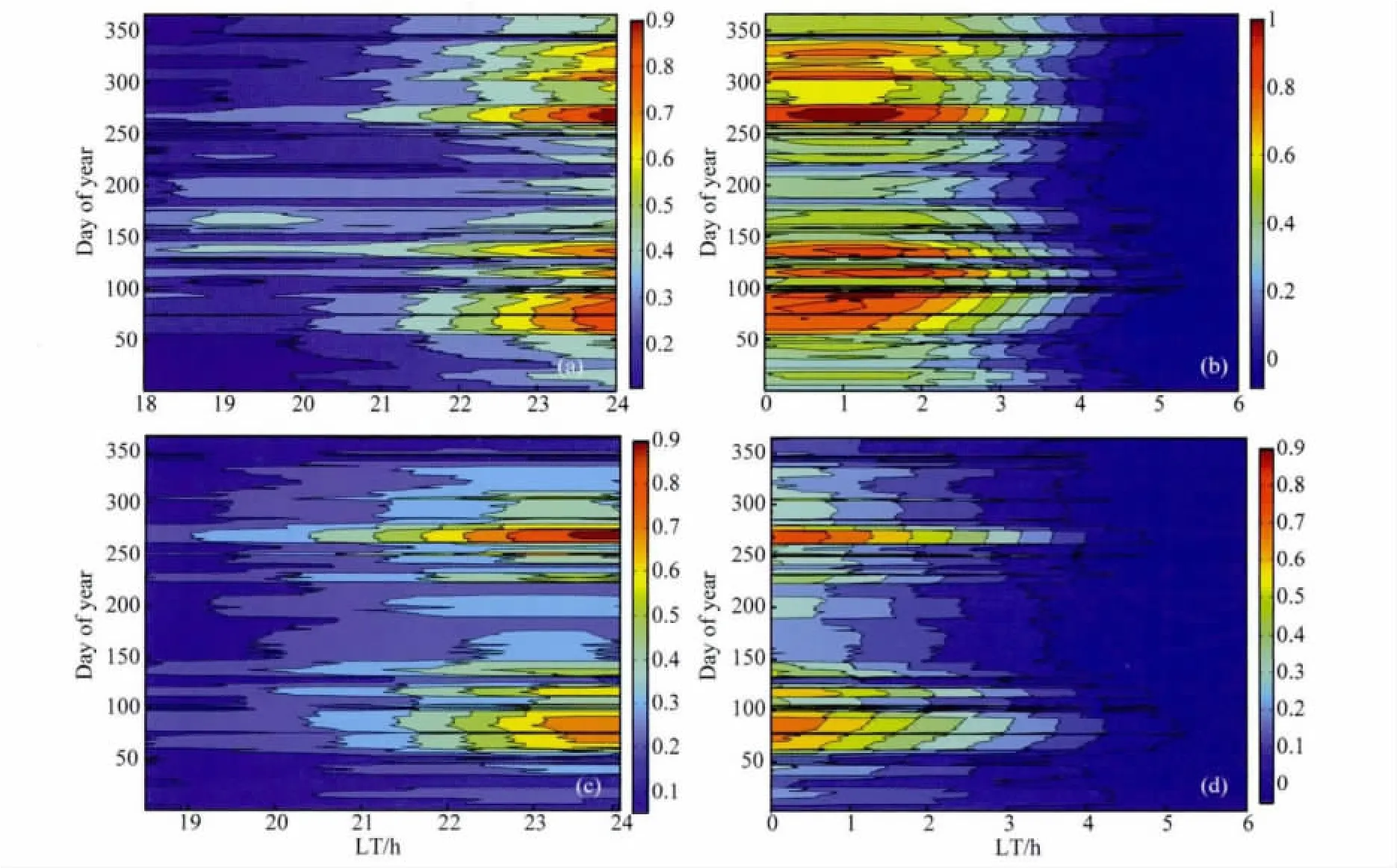
图1 太阳活动高年,线性增长率在午夜之前(a,c)和午夜之后(b,d)随地方时和逐日的变化Fig.1 The variations of linear growth rates depend on local time and day-to-day before the midnight(a,c)and after the midnight(b,d)during high solar activity

图2 太阳活动低年,线性增长率在午夜之前(a,c)和午夜之后(b,d)随地方时和逐日的变化Fig.2 The variations of linear growth rates depend on local time and day-to-day before the midnight(a,c)and after the midnight(b,d)during low solar activity

图3 1997—2007年,线性增长率的平均值随地理经度和季节的变化,增长率的单位为10-3s-1Fig.3 Contours of the average linear growth rates on a month versus geographic longitude in a solar cycle 1997—2007.The unit of growth rate is 10-3s-1
如图4所示,在所有经度区,相比一个太阳活动周内的增长率的平均值(图3),在太阳活动中-高年期间的增长率随季节变化的特征都更为明显,增长率的极大值出现在两分点期间.这可能与增长率受太阳活动的影响有关.
3.3 增长率随太阳活动的变化
图5给出在30°E(a)、120°E(b)、150°E(c)、210°E(d)、240°E(e)和300°E (f)经度区,一个太阳活动周内(1997—2007年),每日线性增长率极大值的逐日变化.图6给出了一个太阳活动周内(1997—2007年),太阳黑子数的逐日变化.
由图5可以看到,在不同经度区,每日线性增长率的极大值均表现出显著的随太阳活动的变化.随着太阳活动的增强(图6),增长率逐渐增大;随着太阳活动的减弱(图6),增长率逐渐减小.在太阳活动峰年(2000—2001年),增长率达到极大值;在太阳活动极小年(1997年和2007年),增长率有极小值.
此外,由图5中也可以注意到,在不同经度区,线性增长率的值存在差异.如图5d和5f所示,在210°E经度区,在太阳活动高年期间,增长率小于0.8×10-3s-1,在300°E经度区,太阳活动高年期间的增长率接近1.6×10-3s-1,约为210°E经度区的值的2倍.
3.4 增长率的逐日变化
图7给出在30°E (a)、60°E (b)、90°E (c)、120°E(d)、150°E(e)、180°E (f)、240°E (g)、270°E (h)、300°E(i)和330°E (j)经度区,线性增长率在太阳活动低年(1997年)、太阳活动中年(2004年)和太阳活动高年(2001年)期间的逐日变化.

图4 1999—2004年,线性增长率的平均值随地理经度和季节的变化,增长率的单位为10-3s-1Fig.4 Contours of the average linear growth rates on a month versus geographic longitude during mid-high solar activity 1999—2004.The unit of growth rate is 10-3s-1
在图7中,整体趋势上看,在不同地理经度区,不同太阳活动期间,增长率均表现出显著的逐日变化特征.在两分点期间(3—4月和9—10月),增长率有极大值.在两至点期间(6—7月和12—1月),增长率有极小值.在太阳活动高年,增长率的值要大于太阳活动中年的增长率;太阳活动中年的增长率又比太阳活动低年的增长率大.
由图7还可以看到,增长率呈现出显著的两分点不对称.在有些经度区,太阳活动低年期间的不对称性较弱,太阳活动高年期间的不对称性更为显著.如图7j所示,在330°E经度区,在太阳活动高年(2001年),3—4月间的增长率的极大值约为1.0×10-3s-1,而9—10月间的增长率的极大值约为1.4×10-3s-1;在太阳活动低年(1997年),3—4月间的增长率的极大值略大于0.2×10-3s-1,而9—10月间的增长率的极大值约为0.4×10-3s-1.在有些地理经度区,如图7b所示的60°E经度区,太阳活动低年期间的不对称也较为显著.在有些经度区,如30°E经度区(图7a)和240°E经度区(图7g),太阳活动低年和太阳活动高年期间的不对称性均不是很显著.在30°E经度区,在太阳活动高年(2001年),3—4月间的增长率的极大值约为0.8×10-3s-1,而9—10月间的增长率的极大值略大于0.8×10-3s-1;在太阳活动低年(1997年),3—4月间的增长率的极大值约为0.2×10-3s-1,而9—10月间的增长率的极大值略大于0.2×10-3s-1;在太阳活动中年(2004年),3—4月间的增长率的极大值略小于0.4×10-3s-1,而9—10月间的增长率的极大值也略小于0.4×10-3s-1.

图5 在不同地理经度区,1997—2007年期间,线性增长率随太阳活动的变化Fig.5 The variations of linear growth rates depend on solar activity in a solar cycle 1997—2007in different geographic longitudinal regions
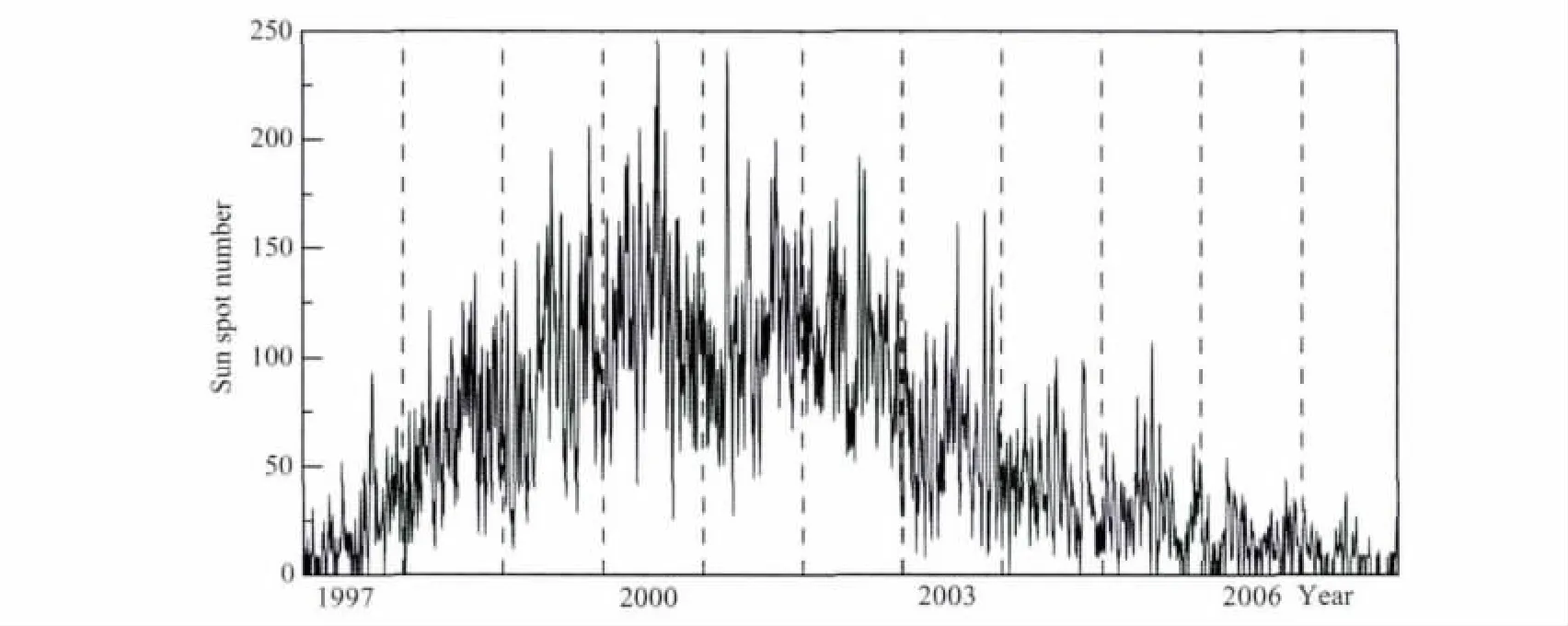
图6 1997—2007年,太阳黑子数的逐日变化Fig.6 The day-to-day variations of sun spot number in a solar cycle 1997—2007
图7所示结果还表明,增长率的逐日变化特征随太阳活动和地理经度变化.在太阳活动高年期间,增长率的逐日变化有较大的起伏,如图7a和7f红色曲线所示.在太阳活动低年期间,增长率的逐日变化的起伏较小.

图7 在不同经度区,不同太阳活动期间,线性增长率的逐日变化Fig.7 The day-to-day variations of the linear growth rates in different geographic longitudinal regions and solar activities
4 增长率与不规则结构和闪烁出现率的比较分析
下面将对前面得到的线性增长率随地方时、季节、太阳活动以及地理经度的变化特征与实验观测结果(等离子体泡和闪烁的出现率)分别进行比较分析.
图8给出2010年3月和4月,在近赤道地区的Lagos(地理经度为3.4°E,地磁纬度为3.03°S)观测到的GPS幅度闪烁出现率和闪烁指数S4随时间的变化[14].
由图8中可以看到,在近赤道地区,GPS闪烁出现于日落之后的几个小时,主要发生于2100—2400LT期间.3—4月的闪烁发生率的极大值出现在2300LT附近.这与图2a给出的太阳活动低年期间(2005年)的线性增长率的极大值出现在2300LT附近较为一致.
图9给出2005年期间,120°E经度区的靠近赤道异常峰的武汉和桂林地区的GPS闪烁发生率随时间的变化[15].
在图9中,武汉地区的闪烁多出现在午夜之后,午夜之前的闪烁发生率的极大值出现在1900LT附近.桂林地区的闪烁集中出现在午夜之前的2000—2400LT期间,这与图2给出的增长率的值在2000—2200LT期间一致.但闪烁出现率的极大值出现于2400LT附近,这与图2给出的赤道附近的增长率随地方时的变化存在一些差异.此外,文献[16]图2给出太阳活动低年的海南地区(磁纬约7°N)的闪烁出现率随地方时的变化,在2000—2100LT出现极大值.这与本文图2c给出的结果一致.这可能意味闪烁出现率随时间的变化还依赖于地磁纬度.

图8 2010年3月(a,c)和4月(b,d),Lagos地区的GPS幅度闪烁出现率和闪烁指数S4随世界时的变化(LT=UT+1h)[14]Fig.8 The occurrences of GPS amplitude scintillation and scintillation index S4vary as UT in Lagos during March(a,c)and April(b,d)2010(LT=UT+1h)[14]
图9 2005年,桂林和武汉两地闪烁出现率随地方时的变化[15]Fig.9 The variations of the occurrences of scintillation depend on the local time in Guilin and Wuhan in 2005[15]
图10给出在靠近磁赤道的低纬地区Peru和Chile,其地理经度分别为 ANC-E(288.7°E)、ANC-W(281.8°E)、ANT-E(294.5°E)和 ANT-W(283°E),闪烁发生率随季节的变化[17].
由图10可以看到,在270°—300°经度区,不同太阳活动期间,闪烁发生率均表现出显著的逐日变化和季节变化.闪烁发生率的极大出现在2—3月和10—11月期间,闪烁发生率的极小出现在5—8月.而且,闪烁发生率还表现出两分点不对称特征.这与图7h和7i中给出的270°E和300°E经度区的线性增长率的变化特征一致.
图11给出2004年8月—2005年7月期间,海南地区(地理经度为109.6°E,地磁纬度约为7°N)的闪烁发生率随季节的变化[18].
由图11可以看到,在近赤道地区的海南,接近120°经度区,在两分点期间,即3—4月和9—10月,闪烁出现率最为频繁.这与图7d给出的增长率随季节变化的特征一致.
另外,文献[19]也指出,在所有经度区,闪烁活动都在两分点期间最为频繁.这与图7给出的线性增长率的变化特征较为一致.
图10和图11的结果表明,线性增长率能较好地反映不同太阳活动期间的闪烁发生率随季节的变化.线性增长率随季节的变化特征可用于表征不规则结构和闪烁发生率随季节变化的特征.
图12给出在不同经度区,DMSP卫星在一个太阳活动周期内观测到的等离子体泡出现率随太阳活动的变化[20].
由图12可以看到,在不同经度区,等离子体泡的出现率均表现出显著的随太阳活动的变化.随着太阳活动增强,等离子体泡的出现率增加;之后,随着太阳活动的减弱,等离子体泡的出现率减小.
比较图12和增长率随太阳活动的变化(图5)发现,增长率能较好地反映等离子体泡的出现率随太阳活动的变化.增长率和等离子体泡的出现率随着太阳活动增强而增加;增长率和等离子体泡的出现率随着太阳活动的减弱而减小.在太阳活动极大期间,增长率和等离子体泡出现率有极大值,在太阳活动极小期间,增长率和等离子体泡出现率有极小值.
图13和图14给出DMSP卫星观测到的不规则结构(等离子体泡)随地理经度的变化.图12为1989—2002年DMSP卫星观测到的等离子体泡的平均出现率[21],图14为太阳活动高年 (1999—2002年)的静日期间,DMSP卫星观测到的等离子体泡的出现率随季节和地理经度的变化[22].

图10 1994—2001年期间,在靠近磁赤道的低纬地区,中等强度闪烁(S4≥0.3)的出现率随季节的变化[17]Fig.10 In low-latitude regions,the percent occurrences of moderate scintillation(S4≥0.3)vary as seasons for years 1994—2001[17]

图11 2004年8月—2005年7月,三亚地区不同强度闪烁发生率的时间变化[18]Fig.11 The percent occurrences of different scintillation activity in Sanya from August 2004to July 2005[18]
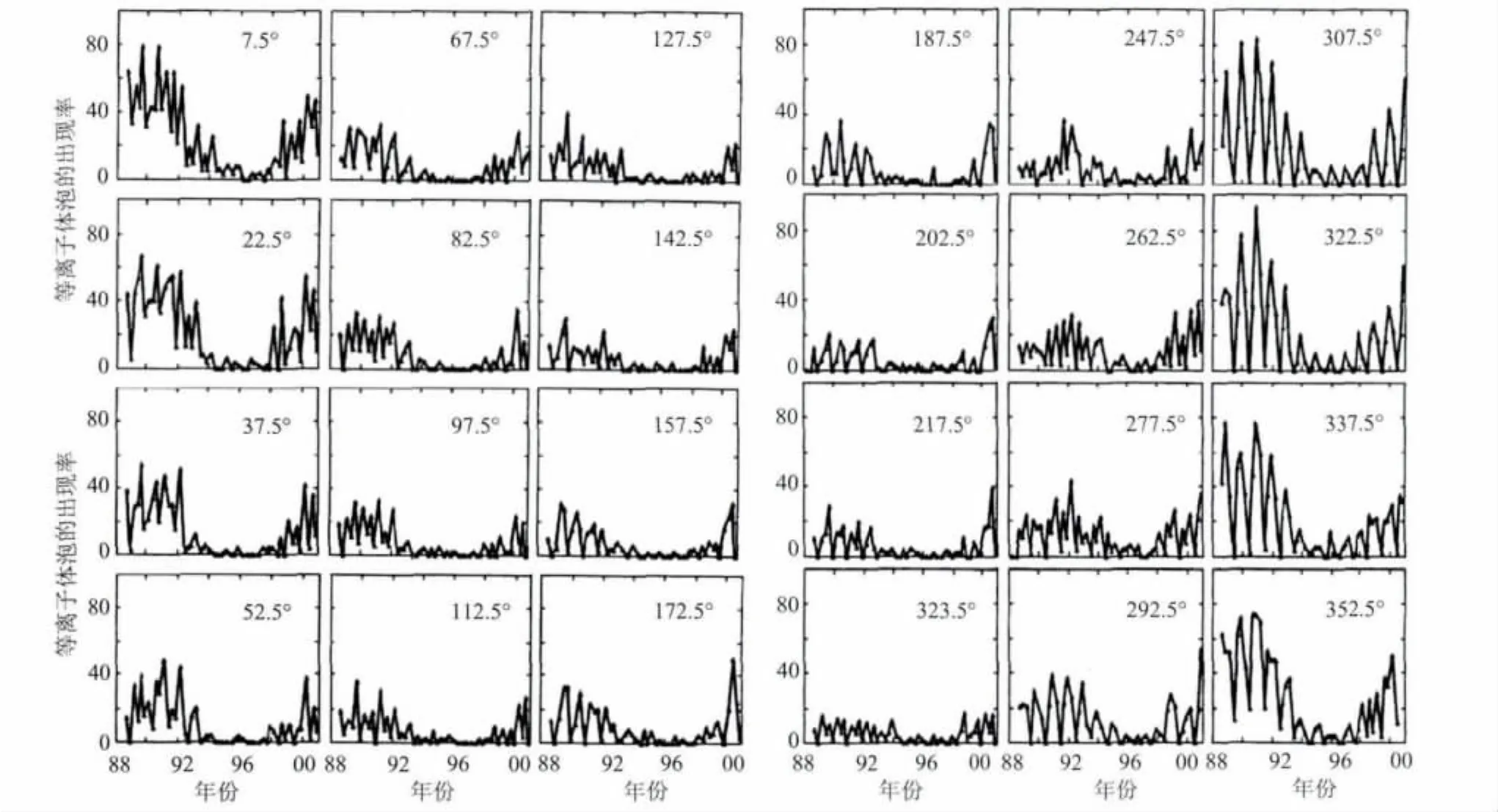
图12 在不同经度区,DMSP卫星观测到的等离子体泡出现率随太阳活动的变化[20]Fig.12 In different longitudinal sectors,the percent occurrence of plasma bubbles measured by DMSP during different solar activities[20]
图13和图14中的卫星观测结果表明,不管是一个太阳活动周的等离子体泡出现率的平均效应,还是太阳活动高年期间的等离子体泡的出现率,均呈现出显著的随经度的变化,在300°E—30°E经度区的3—4月和9—10月期间,等离子体泡的出现率有极大值.0°E—30°E经度区的等离子体泡的出现率较300°E—330°E经度区的等离子体泡的出现率要小.在45°E—135°E经度区和270°E—330°E经度区的6—8月期间,等离子体泡的出现率有极小值.
图13 1989—2002年DMSP卫星观测到的等离子体泡的平均出现率随地理经度和季节的变化[21]Fig.13 The contours of plasma bubble occurrences measured by DMSP satellites between 1989and 2002plotted on a month versus geographic longitude[21]

图14 在太阳活动高年(1999—2002年)的静日期间,DMSP卫星观测到的等离子体泡的出现率随季节和地理经度的变化[22]Fig.14 The contours of plasma bubble occurrences measured by DMSP satellites during high solar activity 1999—2002plotted on a month versus geographic longitude[22]
而且,在不同的经度区,等离子体泡的出现率也表现出随季节的变化.出现率的极大值多出现在3—4月和9—10月期间,出现率的极小值多出现在6—8月.
此外,比较图13和图14也可以看到,一个太阳活动周内的等离子体泡的平均出现率与太阳活动高年期间的等离子体泡的平均出现率存在一定的差异.如在60°E经度区,相比一个太阳活动周内的等离子体泡的季节分布,太阳活动高年期间的等离子体泡的季节变化特征更为明显.
比较图13、图14和图3、图4可发现,广义R-T不稳定性的线性增长率随经度的变化能在一定程度上反映大尺度不规则结构(等离子体泡)出现率的经度变化.增长率的极大值也出现在300°E—30°E经度区的3—4月和9—10月期间.在0°E—30°E经度区,线性增长率在3—4月和9—10月也存在极大值,其值较300°E—345°E经度区的值要小.在45°E—135°E经度区和255°E—330°E经度区的6—8月期间,等离子体泡的出现率有极小值,这与线性增长率的极小值出现在45°E—90°E经度区和255°E—330°E经度区的6—8月期间一致.
在图3和图4中,相比其它地理经度区的值,30°E—210°E经度区的线性增长率较小.而图13和图14中所示的等离子体泡的出现率在30°E—210°E经度区也相对较小.另外,图3和图4的结果与文献[23]图1给出的ROCSAT观测到的1999—2004年期间的不规则结构随地理经度的分布也比较一致.这些表明用三维广义R-T不稳定性线性增长率的经度变化来反映不规则结构的经度变化在某种程度上是可行的.此外,如文献[9]图18所示,通量管积分R-T不稳定性的增长率随经度变化的特征与等离子体泡的出现率随经度变化的特征也较为相似.因此,R-T不稳定性的线性增长率随经度变化的特征可用于表征等离子体泡的经度变化特征.
5 讨 论
如前所述,三维广义R-T不稳定性线性增长率表现出显著的随地方时、季节、太阳活动和地理经度以及逐日变化特征,而且增长率随地方时的变化特征和逐日变化特征还依赖于地理经度和太阳活动.
在不同太阳活动期间和不同地理经度区,如图1和图2所示,增长率的极大值出现的地方时存在差异.在太阳活动低年期间,增长率的极大值出现在日落之后的几个小时,而太阳活动高年期间的增长率的极大值则出现在午夜附近.
如图7所示,增长率的逐日变化特征随太阳活动变化.在太阳活动高年期间,增长率的逐日变化有较大的起伏,如图7a和7f红色曲线所示.在太阳活动低年期间,增长率的逐日变化的起伏较小.在不同地理经度区,增长率的逐日变化特征也存在差异.如在30°E(图7a)和180°E(图7f),增长率的逐日变化有较大的起伏,在330°E(图7i),增长率的逐日变化起伏相对较小.比较图3和图4可以看到,太阳活动中-高年期间的增长率随地理经度和季节的变化特征与一个太阳活动周期内的增长率的变化特征存在一些差异.如在60°E经度区,一个太阳活动周期内的平均增长率随季节变化的特征较弱,而太阳活动中-高年期的增长率随季节变化的特征相对较明显.
一般认为,电子密度与太阳辐射通量存在线性相关关系[24].相比太阳活动低年,太阳活动高年期间的太阳辐射通量以及黑子数的起伏相对较大,这可能使得电离层电子密度的起伏较大,电子密度梯度也会有相应的变化.此外,等离子体垂直漂移速度(电离层背景纬圈电场)也会受到太阳辐射通量的影响[25],太阳活动的起伏会引起等离子体垂直漂移的起伏.如式(3)所示,电子密度梯度和等离子体垂直漂移速度是影响R-T不稳定性线性增长率的两个重要因素.因此,电子密度和等离子体垂直漂移的快速起伏变化会导致增长率的起伏变化,增长率会随太阳辐射通量的变化而起伏.在太阳活动低年,太阳辐射较弱,电子密度和等离子体垂直漂移随季节变化也较小,增长率的季节变化特征相对较弱.在太阳活动高年,太阳辐射较强,导致增长率的季节变化特征较明显.因此,相比太阳活动高年期间的增长率,太阳活动低年期间的增长率随季节变化的特征相对较弱,一个太阳活动周期内的增长率的平均值的季节变化特征也会变得不如太阳高年期间的增长率的变化特征显著,如图3和图4所示.此外,等离子体垂直漂移速度存在随地理经度的变化[26],因此增长率的变化特征也会存在随地理经度的变化.
通过比较分析增长率与实验观测的不规则结构和闪烁活动的变化特征,发现增长率能在一定程度上反映不规则结构和闪烁活动出现率随地方时、季节、太阳活动和地理经度的变化特征以及逐日变化特征,三维R-T不稳定性线性增长率可用于表征不规则结构和闪烁活动随地方时、太阳活动、季节和地理经度变化的形态特征.但需要指出的是,增长率的变化特征与实验观测结果仍然存在一些差异,如不规则结构随地方时的变化特征,特别是在太阳活动低年期间.许多观测结果表明[19,27-30],在太阳活动低年期间,不规则结构主要在午夜之后的0100—0300LT出现,特别是在6—8月期间[27,29-30],它们可能主要由重力波以及大尺度电离层扰动触发[31].在太阳活动高年期间,不规则结构主要在午夜之前出现.而增长率却表明,在太阳活动低年期间,不规则结构在午夜之后较难生成,如图2d所示.在5°E经度区,如图2b所示,在午夜之后的0000—0100LT期间,两分点期间的增长率仍可能为正,而6—8月期间的增长率为负.而在太阳活动高年,不规则结构可能在午夜之后出现,甚至在午夜之后的0100LT附近,增长率会出现极大值.实验结果与增长率之间的这种不一致意味着R-T不稳定性的发展过程与不规则结构的生成和发展过程存在一定的差异.
此外,增长率随地理经度的变化特征与实验观测结果也存在一定的差异,特别是在位于300°E—330°E的南大西洋异常区(South Atlantic Anomaly,SAA).在SAA区,如图13所示,不规则结构的出现率在11—1月期间有一个极大值.虽然计算得到的增长率的值在10—1月期间都较大,但极大值出现在两分点附近.这表明增长率并没有完全反映出不规则结构随地理经度变化的规律.
三维R-T不稳定性线性增长率的变化特征与不规则结构的变化特征之间的差异表明,虽然线性增长率可在一定程度上表征不规则结构随地方时、季节、太阳活动和地理经度以及逐日变化的特征,但仅利用线性增长率很难准确地预测不规则结构和闪烁活动的出现率.这可能是由于影响不规则结构出现的物理因素众多,不规则结构的生成发展过程比较复杂.R-T不稳定性仅仅反映了不规则结构生成和发展的部分过程.
不规则结构的生成发展过程通常可分为三个阶段考虑:种子过程;线性发展阶段;非线性发展阶段.R-T不稳定性线性增长率仅反映了不规则结构的线性发展过程,仅利用线性增长率并不能完全反映不规则结构的变化规律.除了电子密度梯度和等离子体垂直漂移,影响R-T不稳定性的物理因素还包括中性风场、E区电导率、磁偏角以及背景电场和风场的梯度等[10].因此,本文计算得到的线性增长率也并没有完全反映R-T不稳定性的线性发展过程.有关不规则结构和闪烁的一些特殊变化规律,如不规则结构出现率的SAA异常,还有待进一步研究.为了更全面准确地了解和反映不规则结构和闪烁的变化规律,需要结合观测数据以及其它分析方法,并进一步研究影响不规则结构出现的种子过程和非线性发展阶段.对于本文建立的增长率的统计特征模型,也可进一步结合实验观测结果进行改进.如通过比较研究线性增长率与闪烁指数S4的关系,类似于Anderson等[4]建立的等离子体垂直漂移与S4指数之间的关系,构建线性增长率与S4指数之间的联系,进一步改善利用增长率建立的不规则结构和闪烁出现率的理论模型.
6 结 论
本文根据三维广义R-T不稳定性分析得到的线性增长率的表达式,计算在不同地方时、季节、太阳活动和地理经度区的线性增长率,并比较分析增长率随地方时、季节、太阳活动和地理经度区的变化以及增长率的逐日变化与实验观测到的不规则结构和闪烁出现率随地方时、季节、太阳活动和地理经度的变化,具体结果可总结如下:
(1)增长率表现出随地方时的变化,增长率随地方时的变化特征还依赖于太阳活动和地理经度.在太阳活动高年,增长率的极大值主要出现在午夜前2300LT至午夜后0100LT附近;在太阳活动低年,增长率的极大值主要出现在2100—2300LT附近.
(2)在所有经度区,增长率均表现出显著的季节变化.增长率的极大值主要出现在3—4月和9—10月期间;增长率的极小值出现在6—8月和12—1月期间.在不同季节,增长率均表现出显著的随地理经度的变化.在所有经度上,增长率的极大值出现在300°E—30°E经度区的3—4月和9—10月期间,极小值出现在45°E—90°E经度区和255°E—330°E经度区的6—8月期间.
(3)在所有经度区,增长率均表现出显著的随太阳活动的变化.增长率的极大值随着太阳活动的增强而逐渐增大,随着太阳活动的减弱而逐渐减小.在太阳活动极大年期间,增长率的值较大;在太阳活动极小年期间,增长率的值较小.
(4)增长率表现出逐日变化特征,逐日变化特征还依赖于地理经度和太阳活动.在太阳活动高年期间,增长率的逐日变化更为显著.
(5)增长率的变化特征与实验观测结果(不规则结构和闪烁出现率的变化规律)较为一致,但也存在一些差异.三维广义R-T不稳定性线性增长率能在一定程度上反映不规则结构和闪烁出现率随地方时、季节、太阳活动和地理经度的变化以及逐日变化特征.利用线性增长率随地方时、季节、太阳活动和地理经度的变化特征,可构建不规则结构和闪烁活动出现率随地方时、季节、太阳活动和地理经度变化的理论统计特征模型.
本文结果表明三维R-T不稳定性的线性增长率能在一定程度上反映不规则结构的变化特征,这意味着线性增长率可用于预测不规则结构在何时何地出现,并可能应用于闪烁预报模型中[6].这也表明分析R-T不稳定性的线性增长率的变化特征是具有一定科学意义和实际应用价值的.
(References)
[1]Woodman R F.Spread F-an old equatorial aeronomy problem finally resolved?Ann.Geophys.,2009,27(5):1915-1934.
[2]Kelley M C.The Earth′s Ionosphere:Plasma Physics and Electrodynamics(2nd ed).London:Elsevier,2009.
[3]Basu B.On the linear theory of equatorial plasma instability:Comparison of different descriptions.J.Geophys.Res.,2002,107(A8):1199,doi:10.1029/2001JA000317.
[4]Anderson D N,Reinisch B,Valladare C,et al.Forecasting the occurrence of ionospheric scintillation activity in the equatorial ionosphere on a day-to-day basis.J.Atmos.Sol-Terr.Phys.,2004,66(17):1567-1572.
[5]Retterer J M,Decker D T,Borer W S,et al.Assimilative modeling of the equatorial ionosphere for scintillation forecasting:Modeling with vertical drifts.J.Geophys.Res.,2005,110(A11):A11307,doi:10.1029/2002JA009613.
[6]Retterer J M.Physics-based forecasts of equatorial radio scintillation for the communication and navigation outage forecasting system (C/NOFS).Space Weather,2005,3(12):S12C03,doi:10.1029/2005SW000146.
[7]Kelley M C,Retterer J.First successful prediction of a convective equatorial ionospheric storm using solar wind parameters.Space Weather,2008,6(8):S08003,doi:10.1029/2007SW000381.
[8]Singh S B,Patel K,Patel R P,et al.Modeling of VHF scintillation observed at low latitude.J.Physics:Conf.Ser.,2010,208(1):012065,doi:10.1088/1742-6596/208/1/012065.
[9]罗伟华,徐继生,田茂.通量管积分瑞利-泰勒不稳定性的半球不对称和随经度变化的研究.地球物理学报,2012,55(4):1078-1087.Luo W H,Xu J S,Tian M.Investigation of hemispheric asymmetry and longitudinal variation of flux-tube integrated Rayleigh-Taylor instability.Chinese J.Geophys.(in Chinese),2012,55(4):1078-1087.
[10]罗伟华,徐继生,徐良.赤道电离层R-T不稳定性发展的控制因素分析.地球物理学报,2009,52(4):849-858.Luo W H,Xu J S,Xu L.Analysis of controlling factors leading to the development of R-T instability in equatorial ionosphere.Chinese J.Geophys.(in Chinese),2009,52(4):849-858.
[11]Bilitza D.International reference ionosphere 2000.Radio Science,2001,36(2):261-275.
[12]Drob D P,Emmert J T,Crowley G,et al.An empirical model of the Earth′s horizontal wind fields:HWM07.J.Geophys.Res.,2008,113(A12):A12304,doi:10.1029/2008JA013668.
[13]Picone J M,Hedin A W,Drob D P,et al.NRLMSISE-00 empirical model of the atmosphere:Statistical comparisons and scientific issues.J.Geophys.Res.,2002,107(A12):1468,doi:10.1029/2002JA009430.
[14]Adewale A O,Oyeyemi E O,Adeloye A B,et al.A study of L-band scintillations and total electron content at an equatorial station,Lagos,Nigeria.Radio Science,2012,47:RS2011,doi:10.1029/2011RS004846.
[15]徐继生,朱洁,李莉等.武汉与桂林L-波段电波闪烁与TEC起伏特征比较.电波科学学报,2007,22(2):181-186.Xu J S,Zhu J,Li L,et al.Comparison of L-band radio wave scintillations and TEC fluctuations from observation of Wuhan and Guilin.Chinese J.Radio Sci.(in Chinese),2007,22(2):181-186.
[16]胡连欢,宁百齐,李国主.海南地区电离层闪烁观测与GISM模式预测的比较分析.空间科学学报,2007,27(5):384-390.Hu L H,Ning B Q,Li G Z.Comparison between GISM predictions and ionospheric scintillation measurements over Hainan region.Chin.J.Space Sci.(in Chinese),2007,27(5):384-390.
[17]Dandekar B S,Groves K M.Using ionospheric scintillation observations for studying the morphology of equatorial ionospheric bubbles.Radio Science,2004,39(3):RS3010,doi:10.1029/2003RS003020.
[18]熊波,万卫星,宁百齐等.海南三亚地区S4指数与C/N、ROTI的比较分析.地球物理学报,2007,50(6):1639-1648.Xiong B,Wan W X,Ning B Q,et al.A comparison and analysis of the S4index,C/N and ROTI over Sanya.Chinese J.Geophys.(in Chinese),2007,50(6):1639-1648.
[19]Aarons J.The longitudinal morphology of equatorial F-layer irregularities relevant to their occurrence.Space Sci.Rev.,1993,63(3-4):209-243.
[20]Huang C Y,Burke W J,Machuzak J S,et al.Equatorial plasma bubbles observed by DMSP satellites during a full solar cycle:Toward a global climatology.J.Geophys.Res.,2002,107(A12):SIA7-1-SIA7-10,doi:10.1029/2002JA009452.
[21]Burke W J,Gentile L C,Huang C Y,et al.Longitudinal variability of equatorial plasma bubbles observed by DMSP and ROCSAT-1.J.Geophys.Res.,2004,109(A12):A12301,doi:10.1029/2004JA010583.
[22]Gentile L C,Burke W J,Rich F J.A climatology of equatorial plasma bubbles from DMSP 1989—2004.Radio Science,2006,41(5):RS5S21,doi:10.1029/2005RS003340.
[23]Su S Y,Chao C K,Liu C H.On monthly/seasonal/longitudinal variations of equatorial irregularity occurrences and their relationship with the postsunset vertical drift velocities.J.Geophys.Res.,2008,113(A5):A05307,doi:10.1029/2007JA012809.
[24]Liu L B,Wan W X,Chen Y D,et al.Solar activity effects of the ionosphere:A brief review.Chinese Science Bulletin,2011,56(12):1202-1211,doi:10.1007/s11434-010-4226-9.
[25]Fejer B G,Paula E R,Gonzalez S A,et al.Average vertical and zonal F region plasma drifts over Jicamarca.J.Geophys.Res.,1991,96(A8):13901-13906.
[26]Fejer B G,Jensen J W,Su S Y.Quiet time equatorial F region vertical plasma drift model derived from ROCSAT-1 observations.J.Geophys.Res.,2008,113(A5):A05304,doi:10.1029/2007JA012801.
[27]Niranjan K,Brahmanandam P S,Rao P R,et al.Post midnight spread-F occurrence over Waltair(17.7°N,83.3°E)during low and ascending phases of solar activity.Ann.Geophys.,2003,21:745-750.
[28]Burke W J,de La Beaujardière O,Gentile L C,et al.C/NOFS observations of plasma density and electric field irregularities at post-midnight local times.Geophys.Res.Lett.,2009,36(18):L00C09,doi:10.1029/2009GL038879.
[29]Li G Z,Ning B Q,Abdu M A,et al.On the occurrence of postmidnight equatorial F region irregularities during the June solstice.J.Geophys.Res.,2011,116(A4):A04318,doi:10.1029/2010JA016056.
[30]Joshi L M,Patra A K,Rao S V B.Equatorial F-region irregularities during low and high solar activity conditions.Ind.J.Radio Space Phys.,2012,41(2):208-219.
[31]Abdu M A.Equatorial spread F development and quiet time variability under solar minimum conditions.Ind.J.Radio Space Phys.,2012,41(2):168-193.
