无线传感网OFDM 系统中信道估计与均衡技术的算法设计*

郭旻轩，瞿 晓，奚锦程，王 军，张 萌

(东南大学电子科学与工程学院，南京 210096)

正交频分复用OFDM(Orthogonal Frequency Division Multiplexing)是一种高效多载波调制技术，能有效降低多径干扰和信道频率选择性衰落的影响［1］，被认为是4G 无线系统的核心技术之一。目前已应用于数据音频广播、高清晰度数据电视、无线城域网等系统［2－4］。信道估计与均衡是OFDM 系统中关键技术，现有的信道估计与均衡算法如最小二乘法(LS)、最小均方误差法(MMSE)等在精确度或复杂度上不尽如人意。无线传感器网络(WSN)的OFDM 系统中，信道估计可采用基于辅助导频的信道估计方式实现［5］。

1 OFDM 系统

1.1 OFDM 系统简介

OFDM 系统模型如图1所示。在发射端，发送的数据经信道编码，映射，串并转换送入插入导频和虚拟子载波单元，再经过IFFT 完成OFDM 系统的调制操作，添加循环前缀作为保护间隔，通过并串转换将数据送入中频调制的IF 信号;在接收端，经过信道后的数据，进行同步操作，串并转换，去掉循环前缀后送入FFT 完成OFDM 系统的解调操作，对进入频域的数据做信道估计，得到当前实时的信道响应，通过均衡处理以消除信道的影响;随后，再经过解映射和译码最终得到接收的传输码流［6］。其中信道估计与均衡直接影响系统性能。

1.2 信道估计与均衡

设在插入循环前缀前的时间序列为xi，k，变换到频域为在经过信道后为Xi，k，则接收端接受到的信号为Yi，k，则有:

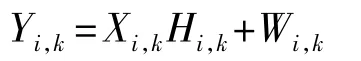
其中，Hi，k是信道对第i个OFDM 符号第k个子载波位置的频率响应，Wi，k是信道对第i个OFDM 符号第k个子载波产生的噪声。

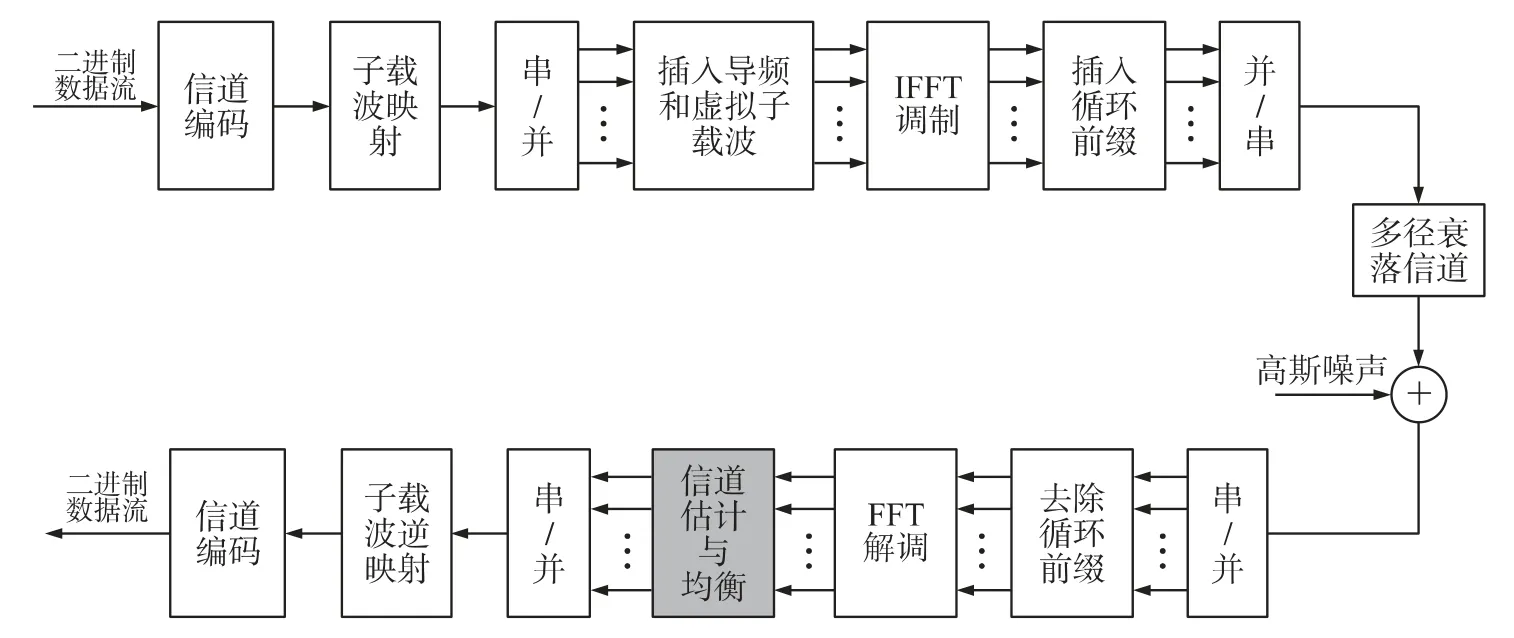
图1 OFDM 系统结构

信道估计的目的在于通过有限的已知数据点估算出整个信道特性Hi，k的估计值～Hi，k，而信道均衡的目的在于通过信道估计得到的～Hi，k，根据接收机接收到的Yi，k计算出原始的发送数据Xi，k。

导频辅助的信道估计常用两种导频图案［7］:块状导频和梳状导频(如图2)。块状导频在若干时间点上的所有频率插入导频，能够适应缓慢衰减的信道。而梳状导频是在所有时间点的若干频率上插入导频，可以适应快速变化的信道，本文选用梳状导频方式。

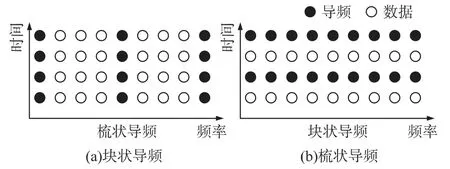
图2 导频图案

2 算法

2.1 经典信道估计算法

经典算法主要有最小二乘法(LS)［8］和最小均方误差法(MMSE)［9］。规定:发送端调制后发出的数据用X 向量表示(频域);接收端接收到的解调前的数据用Y 向量表示(频域);信道频响用H 向量表示;下标p 表示导频;导频个数为Np。列向量Hp表示导频信息经过信道的频响:

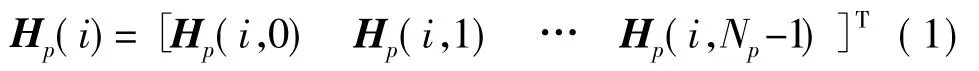
Hp(i，k)表示信道对第i个OFDM 符号中的第k个导频的频域响应。

根据LS 算法，信道估计为:

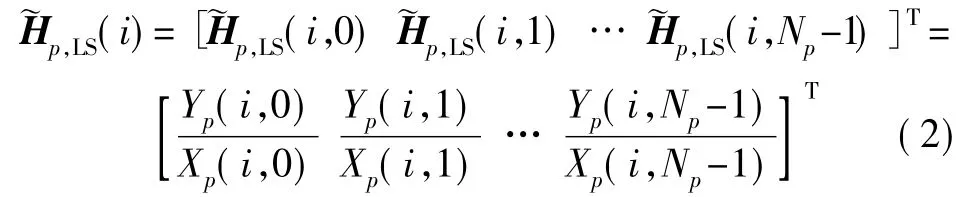
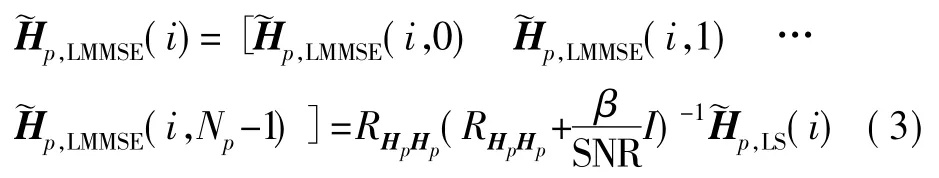
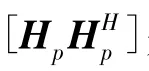
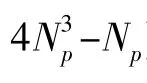
同时，在用LMMSE 进行估计时，自相关矩阵RHpHp和信噪比SNR 的值需要事先设定。这种依赖于经验值的做法非常不利于算法的硬件映射。并且，如果信道改变或者估计错误，会对系统的精确性造成破坏性的影响。

2.2 改进的LMMSE 信道估计算法

针对LMMSE 依赖于经验值的问题，论文“A Study of Channel Estimation for OFDM Systems Capacity for OFDM System and System Capacity for MIMO-OFDM Systems”改进的LMMSE 算法中选择最大的抽头系数MST(The Most Significant Taps)［11］，根据主要路径的特征进行估计RHpHp和SNR，然后计算导频点信道LMMSE 估计值。估计方法如下:

首先计算出时域中的导频响应:

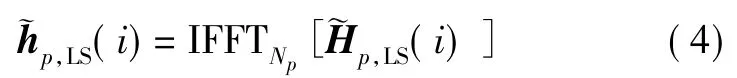
计算得到每个导频附近NMST个OFDM 符号的平均能量:

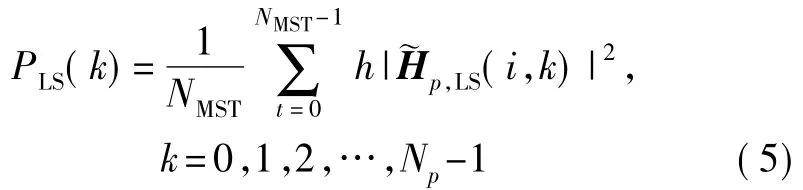
并选出L′个使PLS(k)最大的k，将这些k值组成的集合记为Ω。保留这些导频值，将其余导频的冲击响应(时域)置零。于是可以得到:

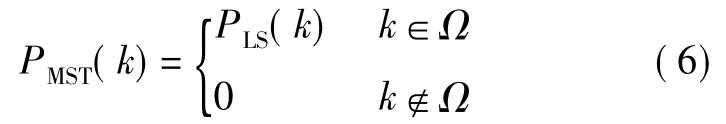
可以证明，估计的自相关矩阵～RHpHp是一个循环矩阵，矩阵的第一行～A 可以这样得到［12］:

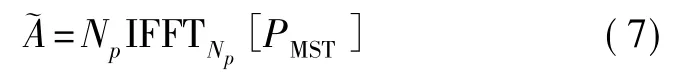
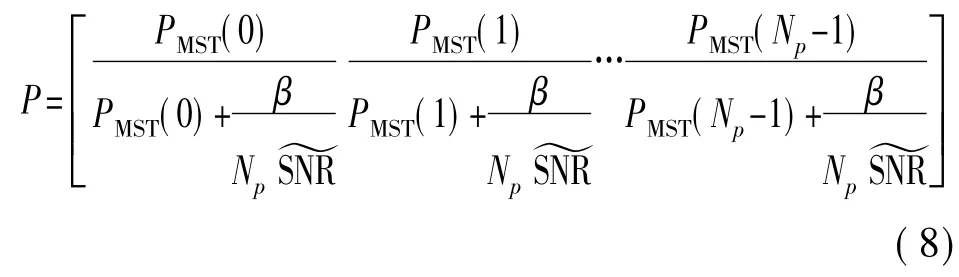
其中估计的信噪比为:

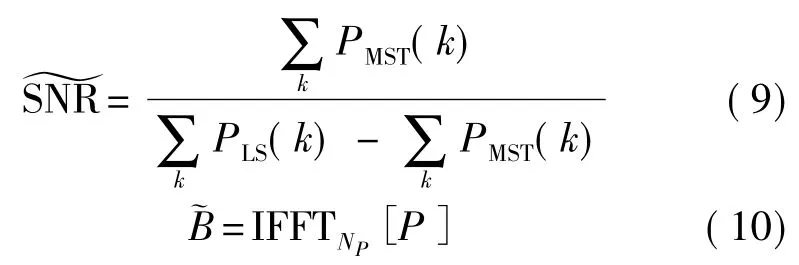
最后得到估计的信道频域响应:

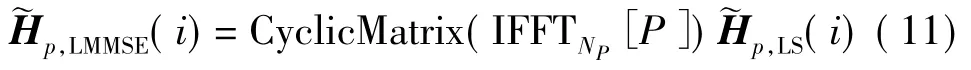
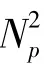
2.3 信道估计与均衡的快速算法

上述的信道估计算法虽然解决了LMMSE 估计中依赖经验值的问题，并且利用循环矩阵降低运算量，但是计算复杂度仍较高。必须注意到的是，上述算法涉及2 次IFFT/FFT 运算，若加上插值，就有3次IFFT/FFT 运算。这种运算非常消耗硬件资源，在做算法的硬件映射时，会大大提升硬件成本并且降低系统的运行速度。

为此，本节设计了以下快速算法(Fast LMMSE)。

注意到式(11)中是循环矩阵与～Hp，LS的相乘，这样的运算可以用循环卷积来代替:

由DFT 运算的共轭对称性及IFFT 与FFT 关联性可以进行如下变换:

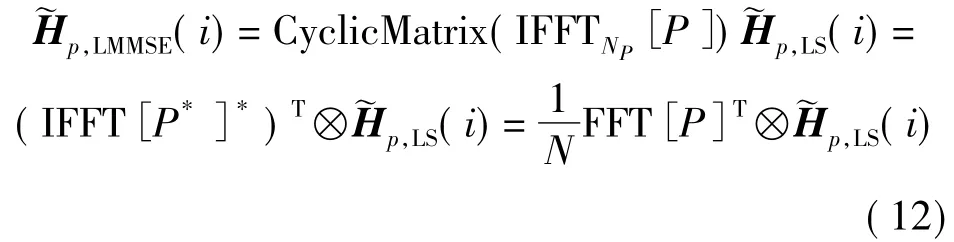
用(·)*表示共轭矩阵，⊗表循环卷积。

由循环卷积特性DFT［f1(k)⊗f2(k)］=DFT［f1(k)］DFT［f2(k)］与二重FFT 运算式FFT{FFT［f(k)］}=Nf((N－k)modN)，k=0，1…(N－1)可得:

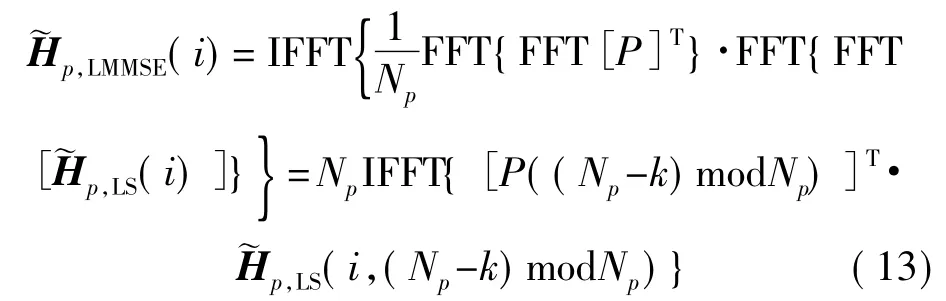
经过这样的化简后不难发现，以移位与向量乘法取代复杂的矩阵乘法化简了运算。此外，结合下文的补零DFT 插值算法，还可以减少两次IFFT 的运算量。

2.4 插值算法

因为导频是呈梳状均匀插入在有效数据中传输的，故得到信道估计矩阵～Hp，LMMSE后，只需对有效数据所在点进行插值便可以得到有效数据对应的信道频域响应。

DFT 插值算法依据时域补零操作等效于频域插值的原理［13］，可以发现FFT和IFFT 运算在之前的运算中包括在整个OFDM 系统中被反复的应用。所以尽管可以进行插值的算法很多，考虑到插值算法对前面算法的承接关系，这里选用基于补零DFT插值。导频点数量为Np(偶数)，相邻导频点间数据点数为Nd，插值过程分3 步进行，具体如下:

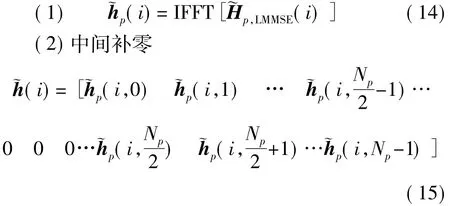
(3)插值得数据点信道频响估计值:

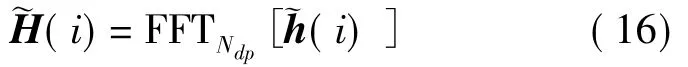
其中Ndp=Np(1+Nd)。对应抽取～H(i)向量中数据点频响估计值便可进行信道均衡。

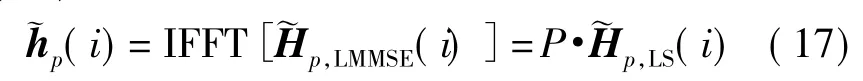
不难发现，结合插值算法后，算法进一优化，比上文改进的LMMSE 算法节省了两次IFFT 运算，仅需一次NpIFFT，一次NdpFFT和一次Np位向量乘法，共(Np/2)lb(Np)+(Ndp/2)lb(Ndp)+3Np+2 次乘除运算和少量加减运算，整个算法复杂度更低，更易于硬件实现。但需注意，此算法适用于导频点等间距的、边缘点均为导频的情形，并非所有的导频图案都适用，因此在具体的导频设计时应该加以注意。

3 OFDM 系统参数与MATLAB 仿真分析

3.1 OFDM 导频结构与算法步骤

结合本文所提出的快速算法，确立OFDM 符号导频结构如图3所示。

图3 OFDM 符号导频结构

在用于发送有用数据的子载波为48个时，最少的IFFT点数为64。为便于后续IFFT 估计和插值计算，每隔7个数据点插入一个到频点。剩余8个不传输数据的虚拟子载波。将这些虚拟子载波分布在直流信道和频谱中央。这样可以消除信号直流成分，节省功率，同时能够降低信号的峰均比0，降低对器件的性能要求。所以56个非零信道映射到64点输入的IFFT 当中采用图4所示指定方式。

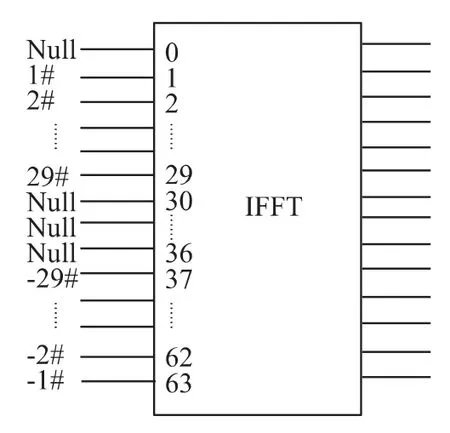
图4 IFFT 输入方式

这种导频结构将使信道估计与均衡算法复杂度更低，更易于电路实现。

3.2 Matlab 仿真

按3.1 节导频结构与上文算法，进行信道估计与均衡的Matlab 仿真以验证其性能。针对无线传感网的特征，仿真信道采用带多普勒频移的6 径瑞利衰落信道，选取参数如表1所示。

我们对文中提及的四种算法进行了Matlab 仿真:分别用四种算法对经过相同信道的相同数据进行信道估计与均衡，并将均衡后的数据与原数据比较，得到的误码率作为衡量算法精确度的标准。为保证仿真结果的可信度并表征算法的效果，我们增加了不经过估计与均衡的数据作为参考组。

仿真结果如图5所示。由图5 可以看出，经验值偏差对LMMSE 算法误码率产生的破坏性影响——它的精确度比LS 算法还要差。而经过改进后的简化算法(Simplified LMMSE)的误码率则明显降低，在信噪比16 dB 时误码率为0.000 2，仅为16 dB 时LS 算法误码率的8.7%。从图中还可以看出，基于改进算法的快速算法(Fast LMMSE)与改进算法的精确度一样，说明我们对算法的改进是无损于其精确度的。

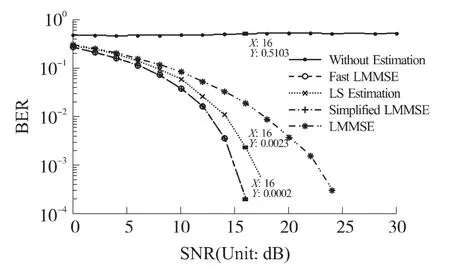
图5 Matlab 仿真结果:误码率－信噪比图线

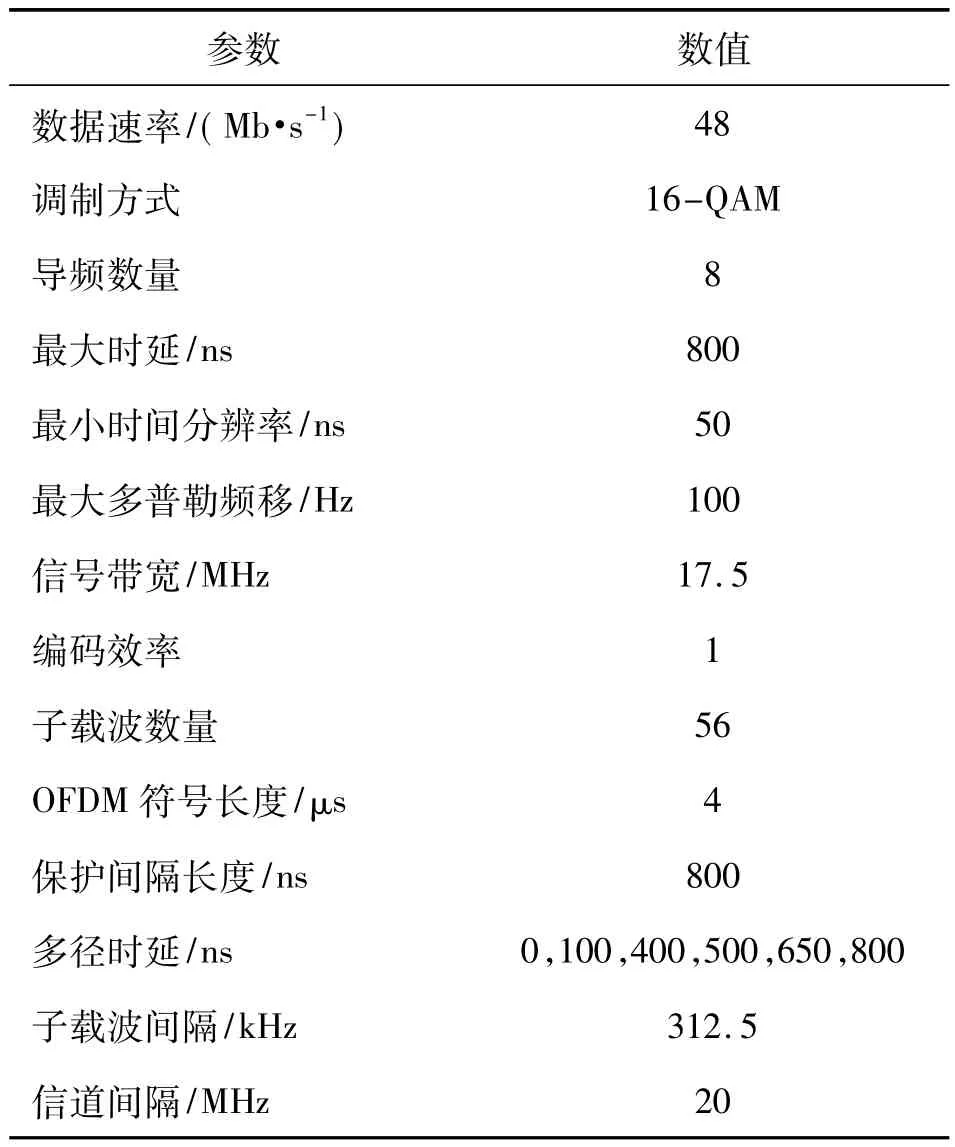
表1 Matlab 仿真参数选择

除精确度意外，我们的另一个关注点，算法复杂度可以通过计算加以比较。在算法的FPGA 实现时，复杂度主要取决于乘除运算，故可用乘除运算次数衡量。各种算法复杂度比较如表2。

由表2，在本文所采用的OFDM 系统64点FFT，8点导频构架时，基于本文改进算法的快速算法复杂度比LS 算法提高8.49%，比LMMSE 降低73.98%，算法复杂度有大幅度降低。同时，算法所达到的误码率表明，结合适当的编码技术以及帧结构后，完全可以满足目前通信系统要求的精确度。

以上结果说明，本文提出的快速算法，在保证信道估计较高性能的同时，降低了运算复杂度，这更利于高性能OFDM 信道估计与均衡器的FPGA 硬件实现。

表2 本文所述几种算法复杂度的比较

4 结束语

本文在分析WSN 的OFDM 系统基于导频辅助信道估计与均衡算法的基础上，改进了LMMSE 算法，并结合DFT 插值算法，设计了一种既有较高精确度又具有较低复杂度的快速算法，避免了复杂的矩阵运算和多余的FFT 运算。确立OFDM 系统64点FFT，8点梳状导频构架，用Matlab 进行系统仿真验证了算法的准确性。进一步的工作将放在信道估计与均衡的FPGA 硬件实现上。

［1］Weinstein S B，Ebert P M.Data Transmission by Frequency-Division Multiplexing Using the Discrete Fourier Transform［J］.IEEE Trans Common，1971，19:628－634.

［2］ETSI，European Telecommunications Standards，Radio Broadcasting Systems.Digital Audio Broadcastingto Mobile，Portable and Fixed Receivers［S］.2nd ed.EN 401 v1.4.1 1997a:493－497.

［3］ETSI，European Telecommunications Standards，Digital Video Broadcasting.Framing Structure，Channel Coding ＆ Modulation for Digital Terrestrial Television［S］.EN 421 v1.1.2，1997b:300－421.

［4］lEEE.IEEE Standard for Local and Metropolitan Area Networks Part 16:Air Interface for Fixed and Mobile Broadband Wireless Access Systems Amendment 2:Physical and Medium Access Control Layers for Combined Fixed and Mobile Operation in Licensed Bands and Corrigendum 1［S］.IEEE Std 802.16e－2005，2006.

［5］张继东，郑宝玉.基于导频的OFDM 信道估计及其研究进展［J］.通信学报，2003，24(11):116－124.

［6］史治国，洪少华，陈抗生.基于XILINX FPGA 的OFDM 通信系统基带设计［M］.杭州:浙江大学出版社2009:1－11.

［7］赵冬，闫发军，王文博.OFDM 系统中导频设置方式对信道估计算法性能的影响［J］.中国无线电，2006，5:57－61.

［8］Jeon W G，Pail K H，Cho Y S，An Efficient Chanel Estimation Technique for OFDM Systems with Transmitter Diversity［J］.Indoor and Mobile Radio Communication，London，UK，2000，9:1246－1250.

［9］Morelli M，Mengali U.A Comparison of Pilot Aided Channel Estimation Methods for OFDM Systems［J］.IEEE Trans Signal Processing，2001，49(12):3065－3073.

［10］Edfors O，Sandell M，van de Beek J J，et al.OFDM Channel Estimation by Singular Value Decomposition［J］.Communications，IEEE Transactions on，1998，46(7):931－939.

［11］Zhou Wen.A Study of Channel Estimation for OFDM Systems Capacity for OFDM System and System Capacity for MIMO-OFDM Systems［D］.Hongkong:University of Hongkong，2010:65－68.

［12］Minn H，Bhargava V K.An Investigation into Time-Domain Approach for OFDM Channel Estimation［J］.Broadcasting，IEEE Transactions on，2000，46(4):240－248.

［13］胡广书.数字信号处理理论、算法和实现［M］.北京:清华大学出版社，2009:137－138.

［14］胡乐.多载波系统降低峰均比技术的研究［D］.南昌:南昌大学，2007:30－30.