一种基于周期模型的物联网实体实时预测方法*

孔英会，沈丹凤

(华北电力大学电子与通信工程系，河北保定 071003)

1 引言

物联网是计算机网络的扩展，是一个实现物物相联的网络。这些物体可以由IP地址嵌入到复杂系统中，通过传感器从周围环境获取信息，并对获取的信息进行响应和处理。它融合了传统网络、传感器、Ad Hoc无线网络、普适计算等的ICT(Information and Communications Technology)技术。随着嵌入式传感器的广泛应用，物联网将信息与通信技术充分应用到各行各业，将传感器嵌入到汽车、家电、电网、桥梁、建筑等物体中，通过网络实现智能物体的互联与信息采集。

当前对传感器感知实体的海量数据和信息进行分析处理成为了物联网应用层发展的基础。实体的状态是人们直接关心的对象，而物联网数据动态性很强，实时变化，存在着不确定性，比如每个对象有一个确定的可能存在性以及对象的属性可能会有不同的可能值，要检测出重要的物联网事件是具有挑战性的［1］。传感器传回来的数据都代表的是过去某一时间的事件，无法呈现人们预想时间的事件情况，物联网中实体的实时状态预测越来越重要。传统预测方法虽取得了大量研究成果，但无法解决不确定性事件的预测问题。如文献［2］中通过时间序列分析中的MWQAR修正模型向前预测信号的变化趋势，文献［3］从消除噪声的角度对传感器输出时间序列进行实时预测并模拟了一个连续信号进行采样处理分析，这些方法对于仅有事件发生记录的传感器并不适用，并不能给人们对于事件是否发生的明确判断。关于事件发生的概率预测，文献［4－5］采用贝叶斯网络预测未来事件发生的概率，基于贝叶斯网络的预测主要事件之间的相关性角度考虑，不适用于独立事件的纵向预测。独立事件的纵向预测需要对事件本身的规律进行研究，文献［6］中采用马尔科夫模型预测未来事件发生的概率，马尔科夫模型用事件现有状态预测将来的状态，与过去事件状态无关，而针对一定周期性发生的事件，将来事件的状态与过去的状态紧密联系，马尔科夫模型不适用。文献［7］中提到了3种关于周期性事件的预测方法，可以解决具有一定周期性的事件预测，但并未做出具体描述及模型建立。文献［8］中对2种预测方法建立了模型，但没有给出具体实现和预测结果。

本文针对有一定周期规律的物联网监测事件预测方法进行研究，首先对传感器返回的原始数据进行统计处理，针对数据规律构建周期预测模型，用过去某段时间的数据作为预测时间窗口预测将来某一时间点状态，同时给出了详细的实现流程与预测结果。实验表明，本预测方法准确性好，系统损耗小，实时性高，因此能根据用户需要为用户提供更有意义的信息。

2 状态预测模型

物联网中传感器返回的数据具有很强的实时性和动态性，利用过去海量的数据建立预测模型预测出将来实时动态的实体状态起到了举足轻重的作用。人类的活动通常是很有规律性的，这些规律从某种角度看都具有很强的周期性。因此，用来感知人类活动的传感器传回的数据通常都显示一定的周期特征［9］。根据这些周期特征，可以利用周期预测模型进行物联网实体实时预测。首先对于传感器状态概率作如下定义。

定义1 特定传感器在特定时间点感知到特定状态的概率是一个由3个参数构成的函数 p，即p(si，tj，ck)∈［0，1］，其中 ck∈C={O，F}，tj∈T，si∈S={s1，s2，s3，…，sn}，S 为所有传感器集合，T 为时间序列集合，C为传感器可能状态集合，即占用(Occupied)和空闲(Free)。由定义1可知，预测需要在时间序列T上建立模型预测函数p的值。

2.1 聚合预测模型(APM)

聚合预测模型［7］(Aggregated prediction model，APM)是3种预测模型中最简单的预测模型。根据文献［7］，本文总结了聚合预测模型的建立过程(见图1)以及概率计算方法。

图1 聚合预测模型序列图Fig.1 Aggregated prediction model sequence diagram

图中，［t0，tc］为建立模型选用的过去一段时间的时间窗口，tp为所需要预测概率的时间点。这个模型计算了时间窗口中传感器状态与预测时间点状态相同的时间占时间窗口总时间的比例。

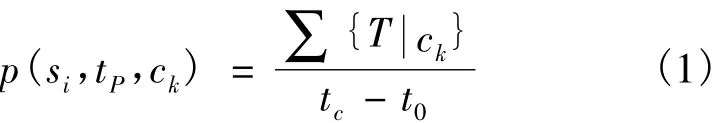
聚合预测模型对于选取的时间窗口的周期模式没有针对性，适用于任何周期模式且原理简单，计算量小，但是该预测模型的预测结果不精确，只能给用户一个大致的导向，不适用于物联网中的决策分析。

2.2 单周期预测模型(SPM)

日常生活中周期性重复事件很多，如果一个事件经过时间段l之后重复了，那么很可能在其他具有相同偏移(相对于时间段l来说)的不同时间点，传感器的感知状态都是相同的［8］。单周期预测模型(Single－ period Prediction Model，SPM)对这种情况具有很好的预测能力。

一般选取的时间窗口为周期l的整数倍，时间窗口大小表示为Tw，预测时间点tp时刻特定状态时，只看时间窗口Tw中与预测时间点tp有相同的相对于l的周期偏移的时间点，预测概率如下:

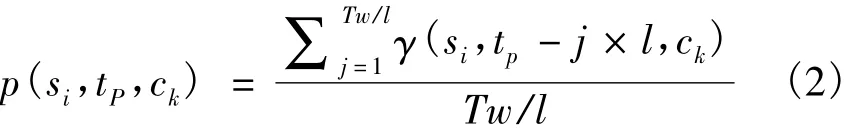
2.3 多周期预测模型(MPM)

实体的实际行为状态中，事件的周期受到多种因素的影响，因此传感器感知到的实体状态很多时候是多周期混合影响的结果，这种情况下如果使用SPM，预测结果将会显得不精确了。因此，对于这种情况多周期预测模型［8］(Multi－ period Prediction Model，MPM)能达到更好的预测效果。

多周期预测模型预测在tp时刻特定状态的概率时，用LStp表示在tp时刻的周期事件，则有LStp=为传感器状态，li为周期，λi为相对周期li的偏移，φi为该事件的概率。在预测tp时刻状态为ci的概率时，用满足条件的概率支持度最大的事件作为最有决定性作用的事件，该事件的概率就是tp时刻传感器输出状态为ci的概率。

MPM中周期事件的发现采用卷积计算周期法［10］，MPM对于周期事件能得到很好的精密的预测结果，但由于卷积周期发现算法涉及多次FFT及逆FFT计算，计算量大，耗时多，不适用于实时性要求高的物联网研究中。

3 预测实现

将以上预测模型运用到物联网实体实时预测，从而通过单个事件周期性发生规律预测出物联网中实体事件发生的概率，判断事件的发生与否，是本文研究的重点，同时也是之前研究并未具体实现的，具有很强的现实意义。

物联网中实体状态实时预测对于实时性以及系统消耗要求较高，需要实时返回预测的状态概率等信息。由以上分析可知，APM的预测结果不精确，不能给用户提供准确的决策支持。MPM中周期事件的发现采用卷积计算周期法，但由于卷积周期发现算法涉及多次FFT及逆FFT计算，计算量大，耗时多，不适用于实时性要求高的系统，而SPM的实时性和精度方面都能满足物联网中实体实时预测的要求。因此，本文重点对SPM实现并进行数据分析。将SPM的思想运用到实际数据中，根据SPM实现事件发生概率预测。本文采用美国三菱电子研究实验室(Mitsubishi Electric Research Labs，MERL)公开的一个大规模传感器数据集作为实验研究对象，通过软件编程实现事件概率预测。

预测流程图如图2所示。首先对研究数据集进行搜索，由传感器的位置确定传感器ID号，对传感器ID号进行筛选出特定位置的传感器数据对象;然后对筛选出的数据逐条遍历，提取出时间窗口中的事件数，由于传感器不断被触发，每次间隔为1.5 s，因此，一个传感器可能会对同一个事件感知到上百条数据，所以这里设定当相邻两个数据间隔时间大于40 min时，则认为是一个新的事件发生，记录下新事件的开始和结束时间点，判断与预测时间点具有相同周期偏移的时间点是否在这些记录下的事件中，若在这些记录下的事件中，则传感器状态统计加一;若不在这些记录下的事件中，则将该事件舍弃，统计出具有相同周期偏移的时间点在这些记录中的个数，从而预测出所需的传感器状态概率。

图2 预测实现流程图Fig.2 Prediction flow chart

4 预测结果分析

本文对实际物联网传感器数据集进行实验，实验数据可以从网站 http://www.merl.com/wmd通过 FTP 获得:ftp://wmd@ftp.merl.com/，username:wmd，password:w0rksh0Pwmd。这些数据是美国三菱电子研究实验室公开的一个大规模传感器数据集。MERL主要是利用了200个传感器来记录实验室两层建筑物办公人员1年内的不同时间不同位置的活动情况。该数据集严格满足周一到周五上班、周末休息的规律，所以它的一个内在的并且起到决定性作用的周期就是一个星期。这样可以节省MPM中周期事件发现而采用的卷积算法而消耗的时间和系统资源，直接采用一星期为一个周期，同时SPM的实时性和精度方面都能满足物联网中实体实时预测的要求。因此，针对物联网的实时性要求，本实验中采用SPM进行预测。

4.1 各个位置的预测结果

本文选取从2006年6月12日00∶00∶00到2006年9月10日23∶59∶59这3个月的7 675 404条数据，来预测2006年9月11日00∶00∶00到2006年9月17日23∶59∶59之间的不同位置传感器状态概率。对8－North conf、Belady Conference room、Nitta Seminar room、Mall这4个地方的10个传感器在2006年9月13日15∶31∶59时间点的状态进行预测的结果如表1所示，其中“O”代表占用，“F”代表空闲，下同。

表1 各位置预测结果Table 1 The predicted results at each point

实验中，将预测概率的临界设为0.5，若预测到占用的概率大于0.5，则认为该传感器在预测时间点是有事件触发的，也即被占用的;若预测到占用的概率小于0.5，则认为该传感器在预测时间点是没有事件触发的，也即空闲的。将这些预测结果与这10个传感器的实际情况做比较，发现该预测结果与实际情况完全符合，因此该预测结果具有很好的指示性。同时搜索预测时间短，与文献［7］中的预测排序均需产生20 s的延迟相比，本方法能在2～4 s之间完成一次搜索预测，大大提高了预测的速度，实时性好，符合物联网实体实时预测的高实时性要求，通过以上概率预测可以及时告知会议室的占用情况，准确性好，且能满足实时搜索预测的要求，从而可以将该方法运用到更多物联网事件预测中，如教室占用情况、道路拥堵情况预测等，为生活生产带来极大的便利。

4.2 各个时间点的预测结果

另外，本文还对kitchen(厨房)2006年9月13日一天内各个时间点占用状态做预测，用2006年6月12日00∶00∶00到2006年9有10日23∶59∶59时间段中每周同一天的相同时间点来进行预测实验，预测各个时间点厨房被占用的概率。实验结果如表2所示。

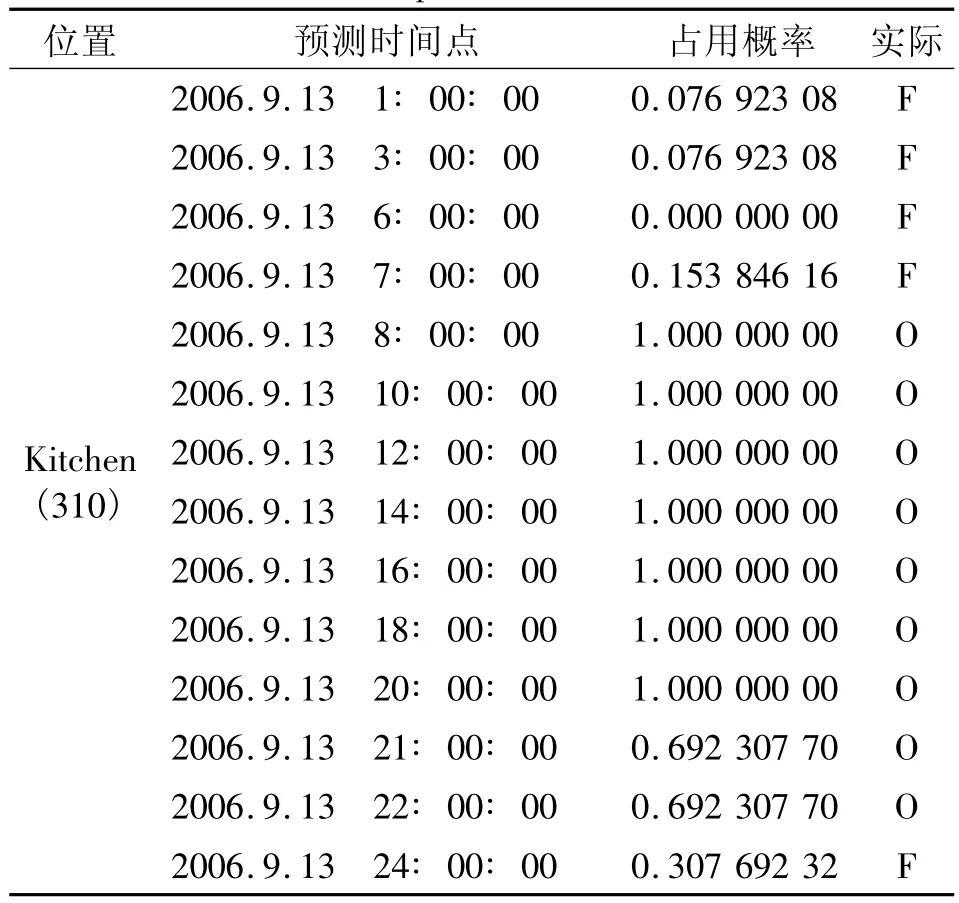
表2 同一位置各时间点结果Table 2 The predicted results of each time point at the same position in kitchen

实验中给定阈值0.5，即预测概率大于0.5的就认为被占用，而小于0.5则认为是空闲状态。同时对2006年9月13日各个时间点的实际占用情况也用数据表示，若实际为占用状态，则概率就为1;若实际为空闲状态，则概率就为0。将表2数据与实际情况拟合成曲线，如图3所示。

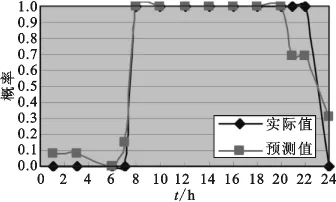
图3 预测值与实际值对比Fig.3 Comparison between the predicted value and the actual value

由图3可得，实际值与预测值的曲线基本符合，其中预测值小于0.5的表示为空闲状态，在实际值中就为0;预测值大于0.5的表示为占用状态，在实际值中就为1，以0.5作为阈值进行归一化之后，预测情况与实际情况完全符合，可以很好地预测出厨房一天中任意时间的占用情况。

相对于文献［7－8］中仅对预测方法的延迟、系统损耗等性能做比较而并未具体实现实体事件概率预测得出具体概率结果来说，通过以上实验方法，可以实现物联网中特定实体的任意时间状态概率预测，能给出预测事件发生的概率数据以及事件发生与否的判断结果。同时，经过与实际情况的比对，得出该预测方法的可靠性和准确度都很高，能满足物联网实时预测的要求。

5 结语

本文针对物联网中实体数据的强实时性和高动态性，对实体将来状态进行了实时预测，介绍了3种预测模型，利用过去海量的数据建立预测模型预测出将来实时动态的实体状态，从而实现了实体实时事件概率的预测以及事件发生与否的判断。其中单周期预测模型能很好地满足物联网实体状态的实时性和动态性，能在2～4 s内完成一次搜索预测，且预测结果精确，均与实际情况吻合，能为人们对物联网实体实时搜索提供很好的指示作用。在以后的研究中，应将周期预测模型运用到更多的物联网实体中，如交通数据流等，以实现更有意义的预测。

［1］ Chen L，Tseng M，Lian X.Development of foundation models for Internet of Things［J］.Frontiers of Computer Science in China，2010，4(3):376－385.

［2］ 姚俊章，余永，葛运建.基于实时预测的传感器信号倍频算法［J］.传感技术学报，2011，24(3):376－381.YAO Jun－zhang，YU Yong，GE Yun－jian.Frequency multiplying algorithm for sensor signal based on realtime predicting［J］.Sensing Technology，2011，24(3):376－381.(in Chinese)

［3］ 刘志成，彭红星.传感器输出时间序列实时预测方法的比较研究［J］.电子测量与仪器学报，2011，25(11):946－951.LIU Zhi－cheng，PENG Hong－xing.Comparison study on real time prediction method of sensor output time series［J］.Electronic Measurement and Instrument，2011，25(11):946 －951.(in Chinese)

［4］ 裘江南，王延章，董磊磊，等.基于贝叶斯网络的突发事件预测模型［J］.系统管理学报，2011，20(1):98－103，108.QIU Jiang－nan，WANG Yan－zhang，DONG Lei－lei，et al.A model for predicting emergency event based on Bayesian Networks［J］.Systems Management Journal，2011，20(1):98 －103，108.(in Chinese)

［5］ Mietz R，Romer K.Exploiting correlations for efficient content－ based sensor search［C］//Proceedings of 2011 IEEE International Conference on Sensors.Limerick:IEEE，2011:187－190.

［6］ Letchner J，Re C，Balazinska M，et al.Access methods for markovian streams［C］//Proceedings of IEEE 25th International Conference on Data Engineering.Shanghai:IEEE，2009:246－257.

［7］ Ostermaier B，Romer K，Mattern F，et al.A real－ time search engine for the web of things［C］//Proceedings of 2010 IEEE International Conference on Internet of Things(IOT).Tokyo:IEEE，2010:1 －8.

［8］ Elahi B M，Romer K，Ostermaier B，et al.Sensor ranking:A primitive for efficient content－based sensor search［C］//Proceedings of 2009 International Conference on Information Processing in Sensor Networks.San Francisco，CA:IEEE，2009:217 －228.

［9］ Reades J，Calabrese F，Sevtsuk A，et al.Cellular census:Explorations in urban data collection［J］.IEEE Pervasive Computing，2007，6(3):30－38.

［10］ Elfeky M G，Aref W G，Elmagarmid A K.Using convolution to mine obscure periodic patterns in one pass［C］//Proceedings of 9th International Conference on ExtendingDatabase Technology. Heraklion，Crete，Greece:IEEE，2004:605 －620.