基于相关特性的改进G－SVSLMS算法*

路翠华，李国林，谢 鑫，奚晓梁

(海军航空工程学院7系，山东烟台 264001)

1 引言

最小均方(LMS)算法计算复杂度低，结构简单，得到了广泛的应用。但它的收敛速度慢，收敛速度与自适应步长和失调之间存在着矛盾。针对这个问题，研究人员先后提出了变步长 LMS 算法［1－3］、LMS牛顿算法［4］、归一化 LMS 算法［5］、变换域及分块LMS 算法［6－8］、截断数据 LMS算法以及最小高阶误差(LMK)算法等［9－10］。目前，LMS 算法已比较成熟，但是结合实际应用可以开展提高其性能的改进算法研究。G－SVSLMS算法是目前比较经典的一种变步长LMS算法，但其步长更新公式易受噪声干扰影响。文献［11］提出基于零均值特性的改进G－SVSLMS算法，提高了G－SVSLMS算法抗零均值白噪声干扰的能力。但高斯白噪声并不都是零均值的，而高斯白噪声的相关性都比较差，本文根据这一特性，提出基于相关特性的改进G－SVSLMS算法，提高了G－SVSLMS算法抗高斯白噪声干扰的能力。

2 G－SVSLMS算法分析

文献［1］提出的G－SVSLMS算法如下:

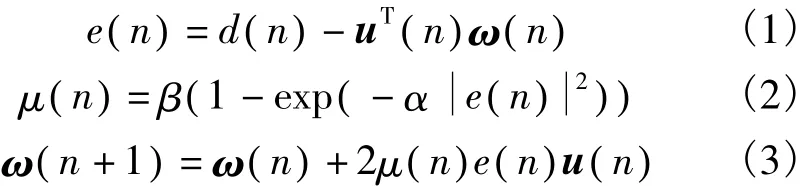
式(2)中，参数α＞0控制函数的形状，参数β＞0控制函数的取值范围，μ(n)与α、β和e( n)的关系如图1所示。当α、β选定时，μ(n)由e( n)唯一确定。

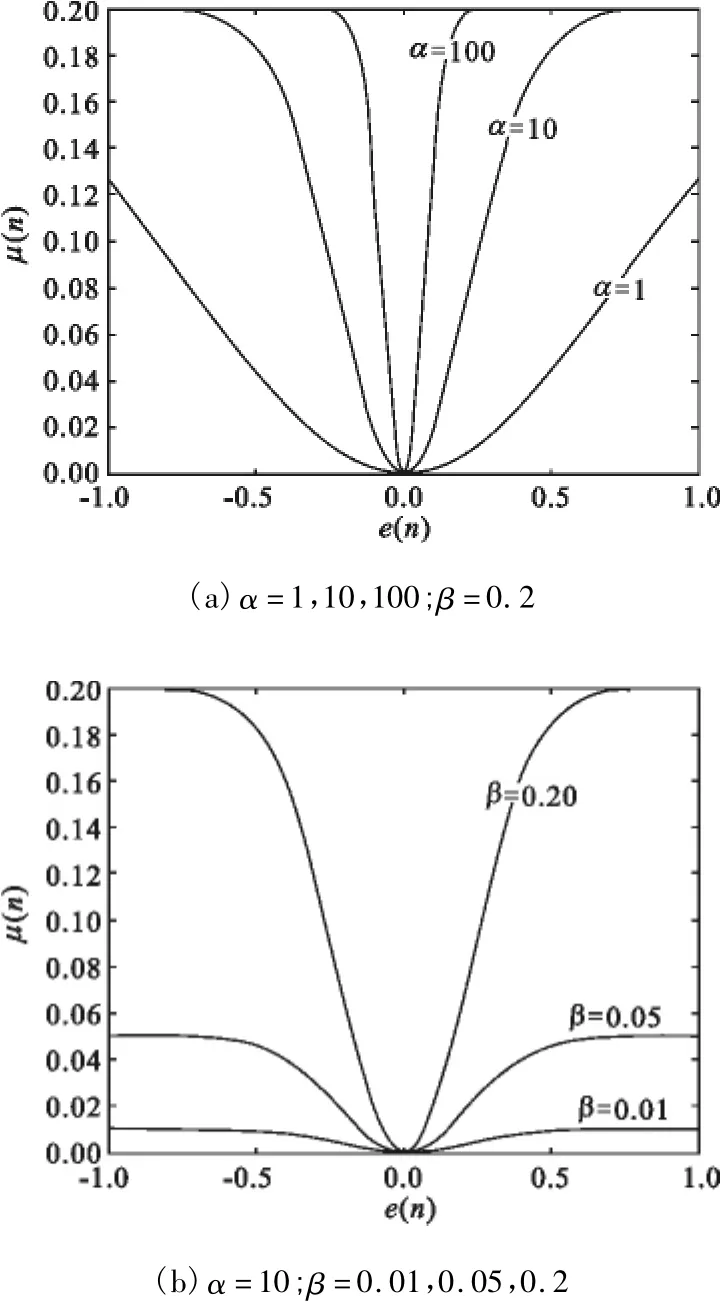
图1 μ(n)与e(n)的关系曲线Fig.1 Curves of μ(n)vs e(n)

G－SVSLMS算法具有较快的收敛速度和较小的稳态误差，但在噪声干扰比较严重的环境中，步长更新公式中的e( n)受噪声的影响，使μ(n)不能达到一个很小的值，从而使自适应算法很难达到最优解，只能在最优解附近波动。

3 基于相关特性的G－SVSLMS算法

高斯白噪声 v的相关性比较差(即E[ v( n) v( n－1 )]=0)，根据这一特性提出基于相关特性的G－SVSLMS算法，其步长更新公式为

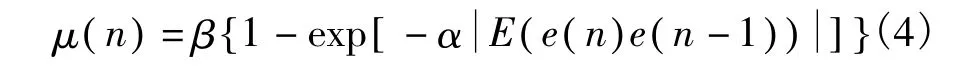
基于相关特性G－SVSLMS算法的步长更新公式相对于G－SVSLMS算法具有较强的抗噪声干扰能力。若两算法选取相同参数α、β，则基于相关特性的G－SVSLMS算法相对于G－SVSLMS算法具有小的稳态误差。

证明如下:

设误差e( n)=s1(n)+v1(n)，其中s1(n)为误差中的信号分量，v1(n)为误差中的噪声分量，则

若信号与噪声不相关，则

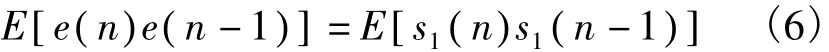
所以基于相关特性G－SVSLMS算法中的步长更新公式受噪声影响很少，具有很强的抗噪声干扰能力。

当算法趋向收敛时，s1(n)→0，所以

则通常情况下，

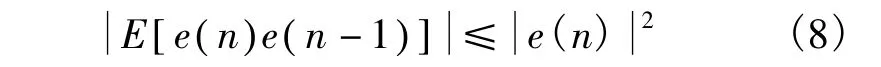
设G－SVSLMS算法步长为μ(n)，基于相关特性的G－SVSLMS算法步长为μ1(n)，若两算法选取相同参数 α、β，由式(2)、(4)、(8)可得

所以此时基于相关特性的G－SVSLMS算法相对于G－SVSLMS算法具有小的稳态误差。

证毕。

在保证算法收敛的条件下，若基于相关特性的G－SVSLMS算法和G－SVSLMS算法参数α相同，基于相关特性的G－SVSLMS算法可以选取相对较大的参数β，从而使基于相关特性的G－SVSLMS算法相对G－SVSLMS算法具有较快的收敛速度。

证明如下:

设G－SVSLMS算法的参数为 α、β，步长为μ(n)，基于相关特性的G－SVSLMS算法的参数为α1、β1，步长为 μ1(n)，输入信号矢量 u(n)相关矩阵为R=E[ u(n) uH(n )]，R的最大特征值为 λmax。

由LMS算法均值收敛条件可得，要使G－SVSLMS算法和基于相关特性的G－SVSLMS算法收敛，须使

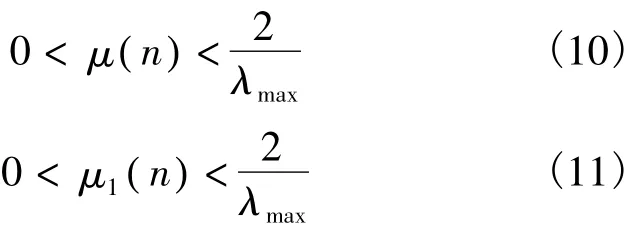
即须使

式中，emax(n)为滤波过程中绝对值最大的误差值。显然

若 α=α1，由式(14)可得，满足式(13)的 β1可大于满足式(12)的β，即若基于相关特性的GSVSLMS算法和G－SVSLMS算法参数α相同，基于相关特性的G－SVSLMS算法可以选取相对较大的参数β1，所以基于相关特性的G－SVSLMS算法相对G－SVSLMS算法具有较快的收敛速度。

证毕。

4 仿真分析

下面将基于相关特性的G－SVSLMS算法和G－SVSLMS算法应用到窄带信号的噪声抑制中，通过仿真验证基于相关特性G－SVSLMS算法的滤波性能。噪声抑制原理如图2所示。

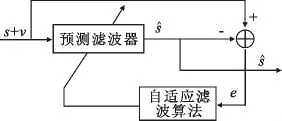
图2 噪声抑制原理Fig.2 Principle of noise suppression

当窄带信号中含有噪声时，由于窄带信号是可预测的，而高斯白噪声的可预测性比较差，可利用其预测性的差异进行噪声抑制。设含有噪声的信号为x，x=s+v，其中s为有用信号，v为噪声。因为s为窄带信号，利用预测滤波器可得到信号s的预测信号^s。误差e=s+v－^s，根据误差e调整滤波器的权值，使^s→s，从而使e→v，达到噪声干扰抑制的目的。

仿真中选取窄带信号为弹目距离大于3倍脱靶量时连续波多普勒无线电引信回波信号。因仿真中只选取了一小段回波信号，可假设在这一小段时间内回波信号的幅度是不变的。在仿真中，信号s是已知的，用平方误差来衡量滤波性能。为有效评价算法性能，选取近似于真实环境的仿真环境，具体如下:设弹目相对运动速度为1 000 m/s，脱靶量为20 m，引信在弹目距离300 m时开始工作。引信回波信号SNR=10 dB时，基于相关特性的GSVSLMS算法和G－SVSLMS算法中参数α=10、β=0.1时，其平方误差曲线如图3所示，收敛曲线如图4所示。

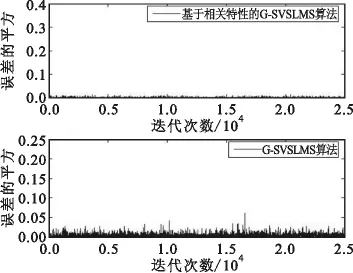
图3 SNR=10 dB、参数相等时平方误差曲线Fig.3 Square error curve when SNR=10 dB and the parameters of two algorithms are equal

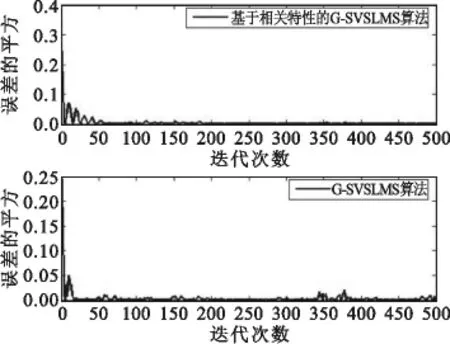
图4 SNR=10 dB、参数相等时收敛曲线Fig.4 Convergent curve when SNR=10 dB and the parameters of two algorithms are equal

由图3和图4可以看出，基于相关特性的改进G－SVSLMS算法和G－SVSLMS算法参数相同时，基于相关特性的改进G－SVSLMS算法收敛速度略慢于G－SVSLMS算法，但其收敛后的稳态误差明显小于G－SVSLMS算法的稳态误差，与理论分析一致。

G－SVSLMS算法中参数 α=10、β=0.01时与基于相关特性的G－SVSLMS算法参数α=10、β=0.1时的稳态误差基本相等，其平方误差曲线如图5所示。

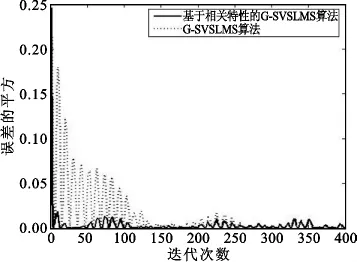
图5 SNR=10 dB、稳态误差相等时平方误差曲线Fig.5 Square error curve when SNR=10 dB and the steady－state errors of two algorithms are equal

由图5可以看出，在保证两种算法收敛后稳态误差基本相等条件下，因基于相关特性的改进GSVSLMS算法可选用较大的参数β，其收敛速度明显快于G－SVSLMS算法，与理论分析一致。

5 结束语

G－SVSLMS算法步长更新公式易受噪声干扰，导致自适应滤波器权值在最优权值附近波动比较大。本文针对这一问题，根据高斯白噪声相关性比较差的特性，对G－SVSLMS算法进行改进，提出了基于相关特性的改进G－SVSLMS算法，使算法抗噪声干扰能力增强。文献［11］提出的基于零均值的改进G－SVSLMS算法只能抵抗零均值高斯白噪声的干扰，而本文提出的算法能抵抗所有高斯白噪声的干扰，但算法抗噪声调幅和噪声调频干扰的性能有待于进一步分析。

［1］ 高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29(8):1094－1097.GAO Ying，XIE Sheng － li.A Variable Step Size LMS A-daptive Filtering Algorithm and Its Analysis［J］.Acta Electronica Sinica，2001，29(8):1094－1097.(in Chinese)

［2］ 周学文，柯熙政.一种新的变步长LMS自适应滤波算法［J］.西安理工大学学报，2006，22(3):290－293.ZHOU Xue－ wen，KE Xi－ zheng.A New Variable Step Size LMS Adaptive Filtering Algorithm［J］.Journal of Xi'an University of Technology，2006，22(3):290 －293.(in Chinese)

［3］ Zheng Fanfan，Huang Lianfen，Shi Zhiyuan，et al.Variable Step－size LMS Adaptive Algorithm Based on Computational Verb Rules［C］//Proceedings of 2010 International Conference on Anti－Counterfeiting Security and I-dentification in Communication.Chengdu:IEEE，2010:343－346.

［4］ Bhotto M Z A，Antoniou A.Improved data － selective LMS－Newton adaption algorithms［C］//Proceedings of the 16th Inernational Conference on Digital Signal Processing.Santorini－ Hellas:IEEE，2009:1 －6.

［5］ Jimaa S A，Al－Simiri A，Shubair R M，et al.Convergence evaluation of variable step－size NLMS algorithm in adaptive channel equalization［C］//Proceedings of 2009 IEEE International Symposium on Signal Processing and Information Technology.Ajman:IEEE，2009:145 －150.

［6］ Qi Lin，Zhang Yanhong，Tao Ran，et al.Adaptive filtering in fractional Fourier domain［C］//Proceedings of 2005 IEEE International Symposium on Microwave，Antenna，Propagation and EMC Technologies for Wireless Communications.Beijing:IEEE，2005:1033 －1036.

［7］ 齐林，周丽晓.变换域自适应滤波算法的研究［J］.郑州大学学报(理学版)，2007，39(1):61－66.QI Lin，ZHOU Li－xiao.Study on Transform －domain A-daptive Filtering Algorithm［J］.Journal of Zhengzhou U-niversity，2007，39(1):61－66.(in Chinese)

［8］ Narasimha M J.Block Adaptive Filter With Time－Domain Update Using Three Transforms［J］.IEEE Signal Processing Letters，2007，14(1):51 －53.

［9］ Haykin S.自适应滤波器原理［M］.4版.郑宝玉.北京:电子工业出版社，2006.Haykin S.Adaptive Filter Theory［M］.4th ed.Translated by ZHENG Bao－ yu.Beijing:Publishing House of E-lectronics Industry，2006.(in Chinese)

［10］ Lu Cui－ hua，Li Guo － lin，Wang Dong － mei.Antinoise Based on Improved Variable Step Size LMS Adaptive Filtering Algorithm［C］//Proceedings of 2010 International Symposium on Image Analysis＆Signal Processing.Taipei:IEEE，2010:82 －84.

［11］ 路翠华，谢鑫，周红梅.基于零均值特性的改进GSVSLMS算法［J］.电讯技术，2013，53(3):284 －287.LU Cui－ hua，XIE Xin，ZHOU Hong － mei.Improved G－SVSLMS Algorithm Based on Zero Mean Characteristics［J］.Telecommunication Engineering，2013，53(3):284 －287.(in Chinese)